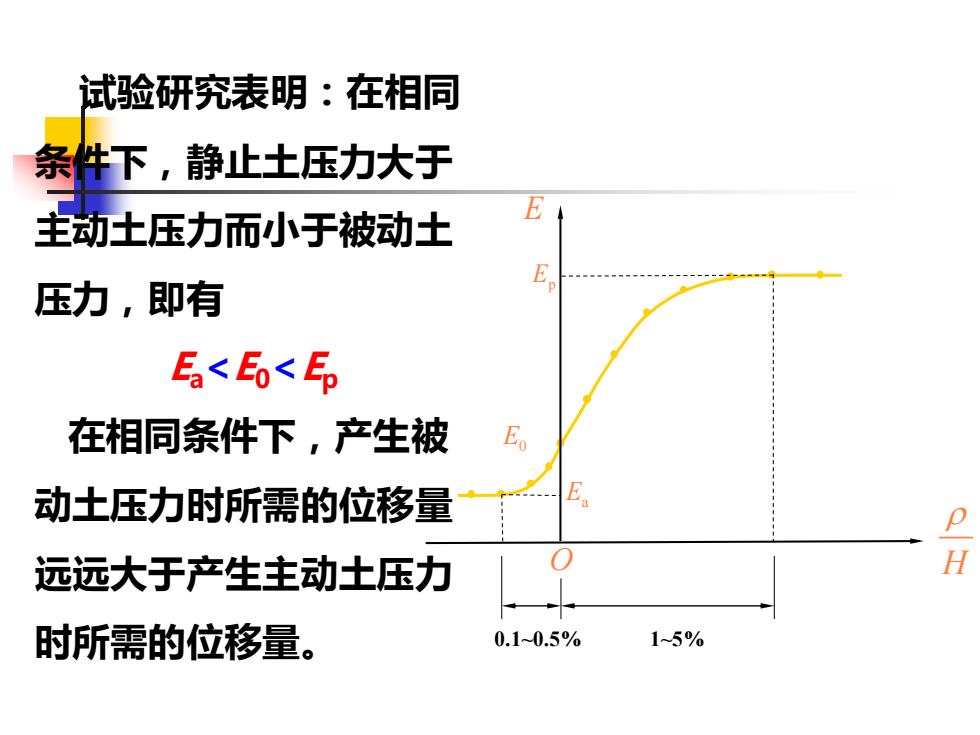
试验研究表明:在相同 条件下,静止土压力大于 主动土压力而小于被动土 压力,即有 E Ea<E0<Ep 在相同条件下,产生被 E 动土压力时所需的位移量 E p 远远大于产生主动土压力 0 H 时所需的位移量。 0.10.5% 15%
E H O E0 Ep Ea 0.1~0.5% 1~5% 试验研究表明:在相同 条件下,静止土压力大于 主动土压力而小于被动土 压力,即有 Ea<E0<Ep 在相同条件下,产生被 动土压力时所需的位移量 远远大于产生主动土压力 时所需的位移量

二静止土压力计算 在填土表面下任意深度处的静止土压力强度可 按下式计算: 由上式可知,静止土压力沿墙高呈三角形分布。 作用在单位墙长上的静止土压力为: E yHK
二.静止土压力计算 在填土表面下任意深度z处的静止土压力强度可 按下式计算: K z 0 0 = 由上式可知,静止土压力沿墙高呈三角形分布。 作用在单位墙长上的静止土压力为: 0 2 0 2 1 E = H K
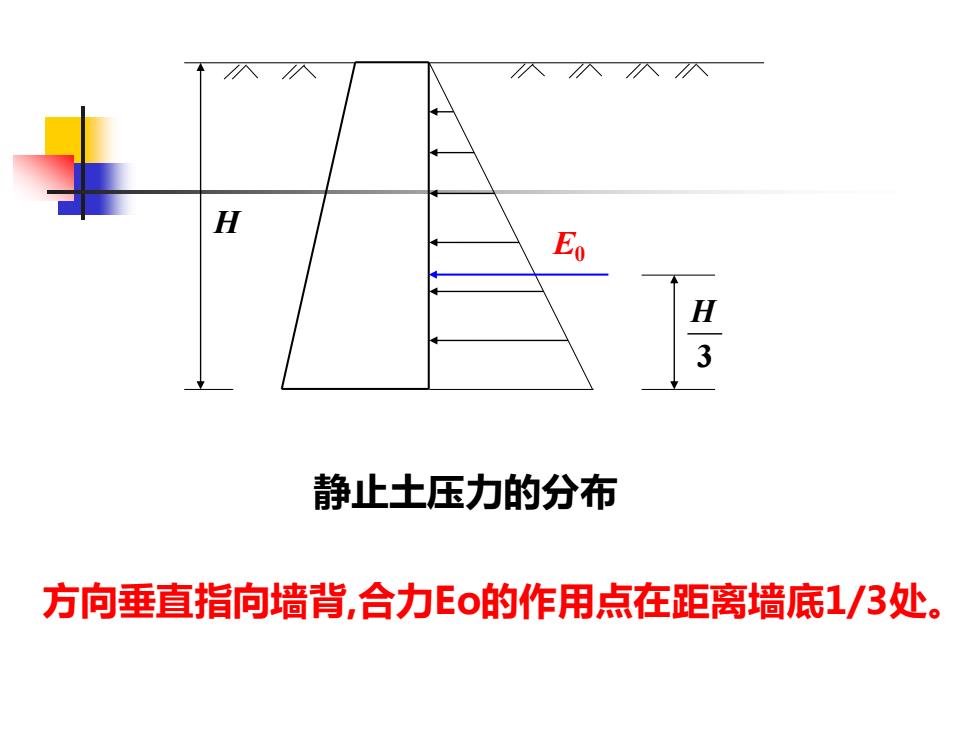
入入入入 H E H 3 静止土压力的分布 方向垂直指向墙背,合力Eo的作用点在距离墙底1/3处
E0 H 3 H 静止土压力的分布 方向垂直指向墙背,合力Eo的作用点在距离墙底1/3处

k。—静止土压力系数,一般应通过试验确定 , 无试验资抖时,可按参考值选取;砂土的k。值为 0.35~0.45;粘性土的k值为0.5~0.7,也可利 用半经验公式k。=1-sino计算。 0一士的有效内摩擦角(): Y一填土的重度,kN/m3; Z一计算点距离填土表面的深度
ko——静止土压力系数,一般应通过试验确定, 无试验资料时,可按参考值选取;砂土的ko值为 0.35~0.45;粘性土的ko值为0.5~0.7,也可利 用半经验公式ko=1-sin 计算。 ′— 土的有效内摩擦角( o); γ —— 填土的重度,kN/m3; Z — 计算点距离填土表面的深度,m。 '

第三节1 郎金土压力理论 基体原理 一认为墙后填主达到极限平衡状态时,与墙背接触 的任一土单元体都处于极限平衡状态,然后根据土单 元体处于极限平衡状态时应力所满足的条件来建立土 压力的计算公式 基本假定 。挡土墙的墙背垂直; 。挡土墙的墙后填土表面水平; 。挡土墙的强背光滑;
第三节 郎金土压力理论 基本原理 认为墙后填土达到极限平衡状态时,与墙背接触 的任一土单元体都处于极限平衡状态,然后根据土单 元体处于极限平衡状态时应力所满足的条件来建立土 压力的计算公式. 基本假定 ❖ 挡土墙的墙背垂直; ❖ 挡土墙的墙后填土表面水平; ❖ 挡土墙的强背光滑;