
左递归的消除 。左递归的定义 如果一个文法中有非终结符号A使得AA,那么这 个文法就是左递归的 立即左递归(规则左递归) 文法中存在一个形如A→Ax的产生式 ·自顶向下的语法分析技术不能处理左递归的情况, 因此需要消除左递归,但是自底向上的技术可以 处理左递归 28
左递归的消除 • 左递归的定义 – 如果一个文法中有非终结符号A使得A Aα,那么这 个文法就是左递归的 • 立即左递归 (规则左递归) – 文法中存在一个形如A → Aα的产生式 • 自顶向下的语法分析技术不能处理左递归的情况, 因此需要消除左递归,但是自底向上的技术可以 处理左递归 28 南大编译许畅
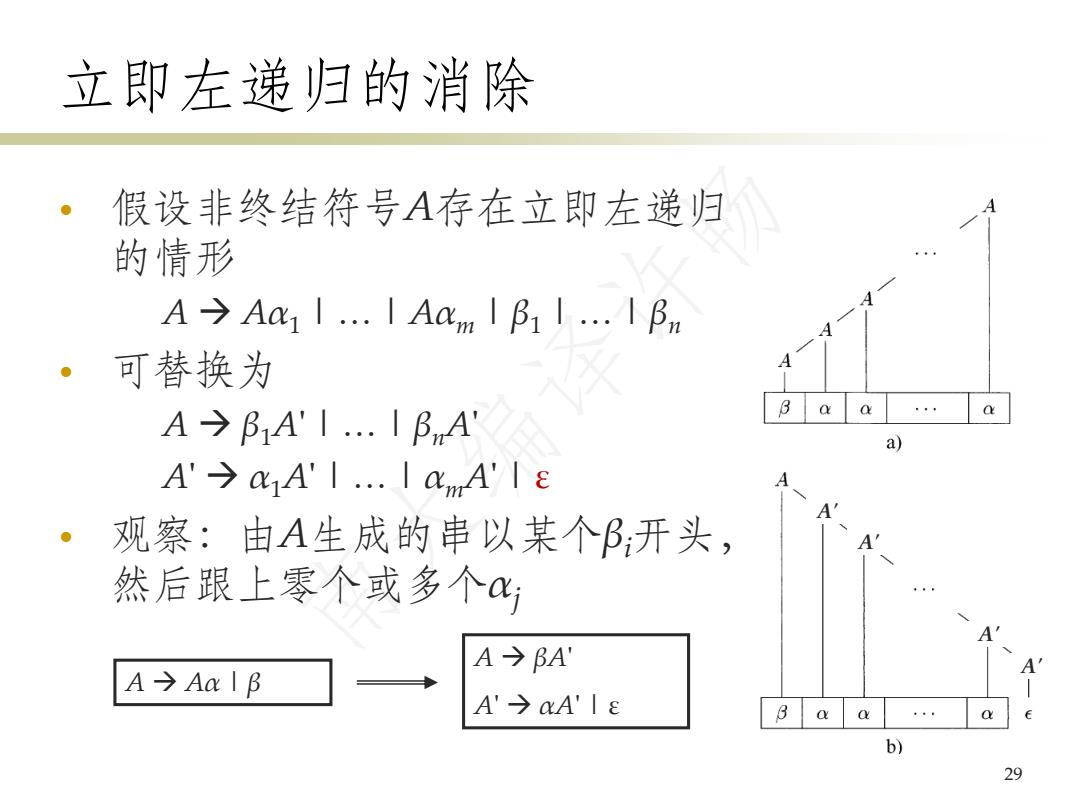
立即左涕归的消除 假设非终结符号A存在立即左递归 的情形 A→A11…1AmIβ1I..Iβ A 。可替换为 A A→B1A'I..IB,nA' a a) A'→01A'I.IXmA'|E 观察:由A生成的串以某个B:开头, 然后跟上零个或多个x; A A→BA' A→AaIB A'→aA'Ie 3 b) 29
立即左递归的消除 • 假设非终结符号A存在立即左递归 的情形 A → Aα1 | … | Aαm | β1 | … | βn • 可替换为 A → β1A' | … | βnA' A' → α1A' | … | αmA' | ε • 观察:由A生成的串以某个βi开头, 然后跟上零个或多个αj 29 A → Aα | β A → βA' A' → αA' | ε A' A' A' 南大编译许畅 A

立即左递归消除示例 E→TE E→E+T|T E'→+TE'|∈ T→T*F|F T→FT' F→(E)|id T'*FT'I∈ F→(E)Iid 30
立即左递归消除示例 30 南大编译许畅

消除多步左涕归 ·消除立即左递归的方法并不能消除因为多步推导 而产生的左递归 文法:S→Aa I b A→Ac丨SdIe S=>Aa=>Sda ·如何消除? 31
消除多步左递归 • 消除立即左递归的方法并不能消除因为多步推导 而产生的左递归 – 文法:S → Aa | b A → Ac | Sd | ε – S => Aa => Sda • 如何消除? 31 南大编译许畅

通用的左递归消除方法 输入:没有环和ε产生式的文法G 0 输出:等价的无左递归的文法 步骤 将文法的非终结符号排序为A1,A2,,Am for i=1 to n do{ for j=1toi-1 do{ 将形如A;→Ay的产生式替换为A:→01y|δ2y|.…10Y, 其中A→δ1|δ2I.|δk是以A为左部的所有产生式 消除A的立即左递归 32
通用的左递归消除方法 • 输入:没有环和ε产生式的文法G • 输出:等价的无左递归的文法 • 步骤 将文法的非终结符号排序为A1 , A2 , …, An for i = 1 to n do { for j = 1 to i – 1 do { 将形如Ai → Ajγ的产生式替换为Ai → δ1γ | δ2γ | … | δkγ, 其中Aj → δ1 | δ2 | … | δk是以Aj为左部的所有产生式 } 消除Ai的立即左递归 } 32 南大编译许畅