
二义性(2) 程序设计语言的文法通常是无二义的 否则就会导致一个程序有多种“正确”的解释 如文法E→-EIE+EIE*EI(E)Iid应对句子a+ b*C时 有些二义性的情况可以方便文法或语法分析器的 设计 但需要消二义性规则来剔除不要的语法分析树 比如:先乘除后加减 18
二义性 (2) • 程序设计语言的文法通常是无二义的 – 否则就会导致一个程序有多种“正确”的解释 – 如文法 E → – E | E + E | E * E | ( E ) | id 应对句子 a + b * c 时 • 有些二义性的情况可以方便文法或语法分析器的 设计 – 但需要消二义性规则来剔除不要的语法分析树 – 比如:先乘除后加减 18 南大编译许畅

词法分析和语法分析的比较 阶段 输入 输出 描述体系 词法分析 源程序符号串 词法单元序列 正则表达式 语法分析 词法单元序列 语法分析树 上下文无关文法 19
词法分析和语法分析的比较 阶段 输入 输出 描述体系 词法分析 源程序符号串 词法单元序列 正则表达式 语法分析 词法单元序列 语法分析树 上下文无关文法 19 南大编译许畅

上下文无关文法和正则表达式(1) 上下文无关文法比正则表达式的能力更强 所有的正则语言都可以使用文法描述 但有一些用文法描述的语言不能用正则表达式描述 证明 首先S→aSb ab描述了语言L{ambn I n>0},但这个N 语言无法用DFA识别 假设有DFA识别此语言L,且这个DFA有k个状态。那么在识 别a+1..的输入串时,必然两次到达同一个状态。假设自动机 在第i个和第j个a时进入同一个状态,那么:因为DFA识别L, abj必然到达接受状态,因此abi必然也到达接受状态。 。直观地讲:有穷自动机不能计数 20
上下文无关文法和正则表达式 (1) • 上下文无关文法比正则表达式的能力更强 – 所有的正则语言都可以使用文法描述 – 但有一些用文法描述的语言不能用正则表达式描述 • 证明 – 首先S → aSb | ab描述了语言L { a nb n | n > 0 },但这个 语言无法用DFA识别 • 假设有DFA识别此语言L,且这个DFA有k个状态。那么在识 别a k+1…的输入串时,必然两次到达同一个状态。假设自动机 在第i个和第j个a时进入同一个状态,那么:因为DFA识别L, a jb j必然到达接受状态,因此a ib j必然也到达接受状态。 • 直观地讲:有穷自动机不能计数 20 南大编译许畅

上下文无关文法和正则表达式(2) 证明(续) 任何正则语言都可以表示为上下文无关文法的语言 任何正则语言都必然有一个NFA,对于该NFA构造如 下的上下文无关文法 对NFA的每个状态i,创建非终结符号A; 如果有在输入a上到达j的转换,增加产生式A;→aA; 如果i在输入ε上到达j,那么增加产生式A:→A 如果i是一个接受状态,增加产生式A:→ε 如果i是开始状态,令A为所得文法的开始符号 21
上下文无关文法和正则表达式 (2) • 证明 (续) – 任何正则语言都可以表示为上下文无关文法的语言 – 任何正则语言都必然有一个NFA,对于该NFA构造如 下的上下文无关文法 • 对NFA的每个状态i,创建非终结符号Ai • 如果有i在输入a上到达j的转换,增加产生式Ai → aAj • 如果i在输入ε上到达j,那么增加产生式Ai → Aj • 如果i是一个接受状态,增加产生式Ai → ε • 如果i是开始状态,令Ai为所得文法的开始符号 21 南大编译许畅
NFA构造文法的例子 ·A>aAo I bAo l aA1 ·A1→bA2 ·A2→bA3 ·A3→E 考虑baabb的推导和接受过程可知:NFA接受一个句子 的运行过程实际就是该文法推导出该句子的过程 start b b 3 b (alb)*abb 22
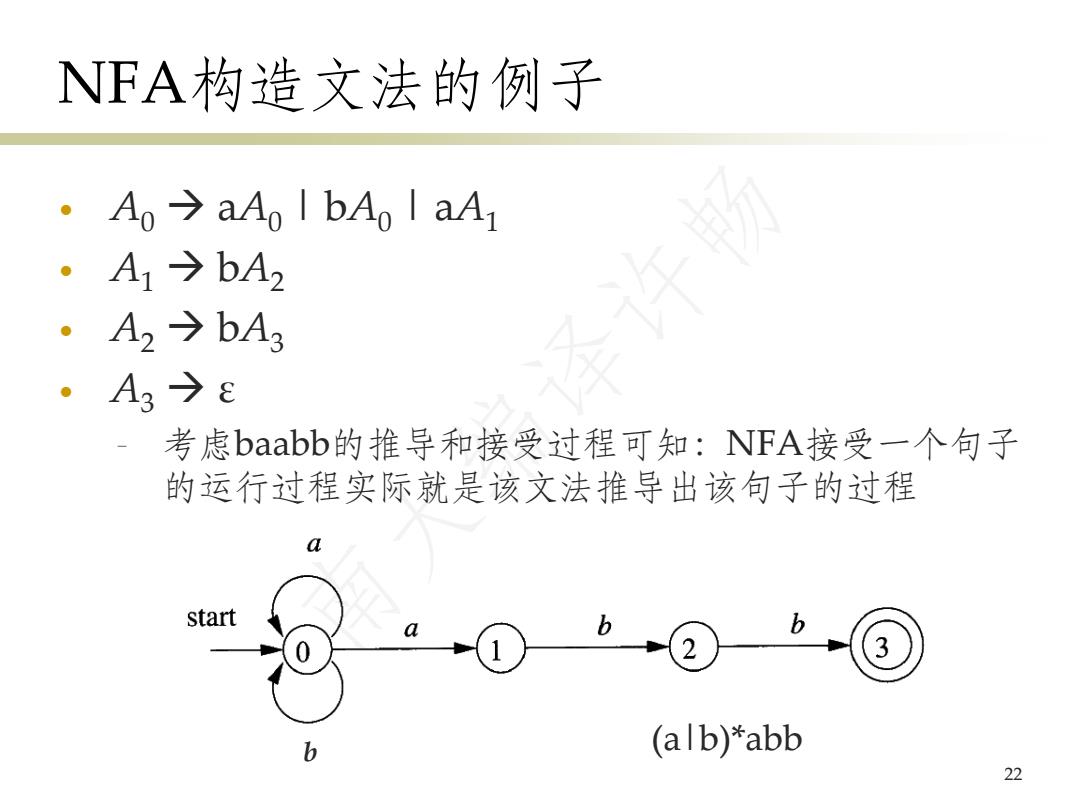
NFA构造文法的例子 • A0 → aA0 | bA0 | aA1 • A1 → bA2 • A2 → bA3 • A3 → ε – 考虑baabb的推导和接受过程可知:NFA接受一个句子 的运行过程实际就是该文法推导出该句子的过程 22 (a|b)*abb b 南大编译许畅