
问题4: ·有限有补分配格一定有2n个元素 因为B1,B2,B3,..,Bn有2n个元素? 其实,我们还可以这样来观察: 1,这样的格中,原子个数是n个 2,除0外,所有元素都可以表示为一个或者多个原子的 join,所有由一个或者多个原子的join的结果都是格中元素。 3,这样的元素有2n.1个
问题4: • 有限有补分配格一定有2 n个元素 因为B1,B2,B3,…,Bn有2 n个元素? 其实,我们还可以这样来观察: 1,这样的格中,原子个数是n个 2,,除0外,所有元素都可以表示为一个或者多个原子的 join,所有由一个或者多个原子的join的结果都是格中元素。 3,这样的元素有2 n -1个
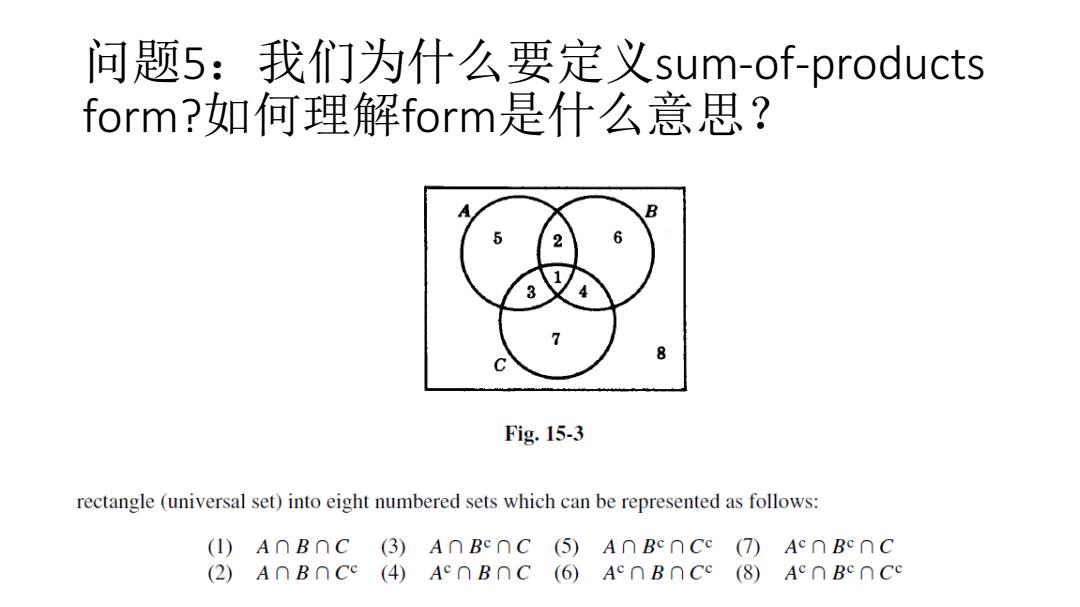
问题5:我们为什么要定义sum-of-products form?如何理解form是什么意思? Fig.15-3 rectangle(universal set)into eight numbered sets which can be represented as follows: (I)A∩B∩C(3)A∩Bc∩C(5)A∩Be∩Cc(T)Ac∩Bc∩C (2)A∩BnCe(4)Ac∩B∩C(6)Ac∩BnCe(8)Ac∩BenCc
问题5:我们为什么要定义sum-of-products form?如何理解form是什么意思?

问题6:任意的布尔代数运算表达式,是否都 可以表达为某个"sum-of-products form"? E=(x+y)+(xyz+x'y)'and E2=((xy'z+y)'+x'z)' Theorem 15.8:Every nonzero Boolean expression EE(x1,x2,...,x)is equivalent to a complete sum-of-products expression and such a representation is unique. 这个定理为我们证明两个逻辑(布尔)表达式的等价带来了极大的便利!
问题6:任意的布尔代数运算表达式,是否都 可以表达为某个”sum-of-products form”? 这个定理为我们证明两个逻辑(布尔)表达式的等价带来了极大的便利!

复习几个概念: Literal?Fundamental product?Contained in? E=xz'+y'z+xyz'and E2=xz+x'yz'+xy'z Contained in? Observe that if P is contained in P2.say P2=P*then,by the absorption law. P1+P2=P1+P1*Q=P Thus,for instance,x+x'y=x
复习几个概念: Literal?Fundamental product?Contained in? Contained in?