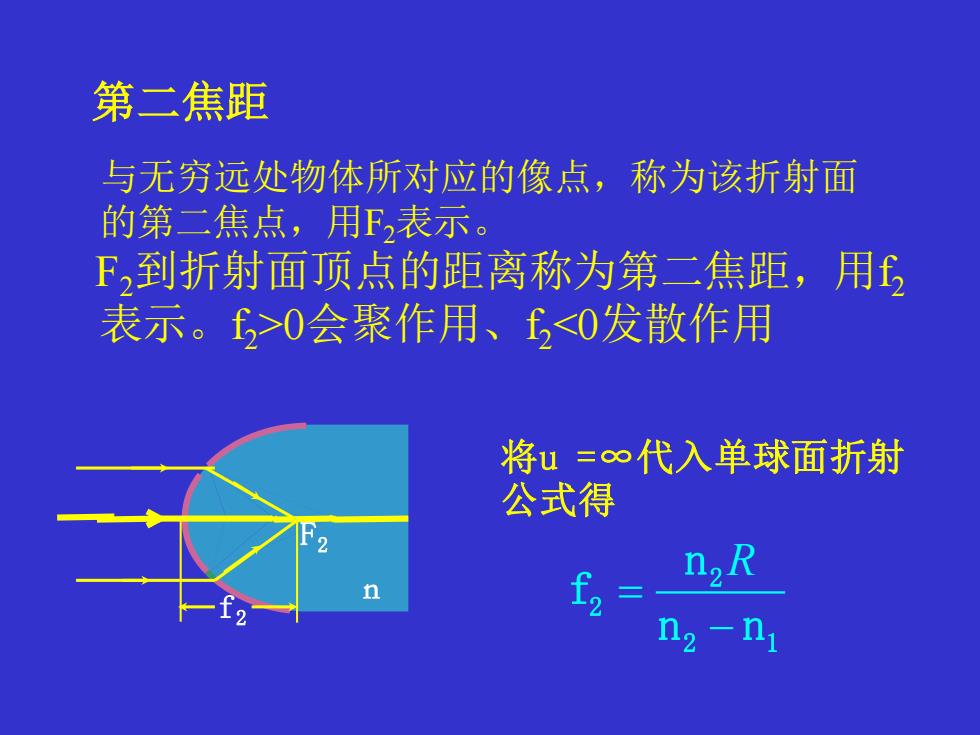
第二焦距 与无穷远处物体所对应的像点,称为该折射面 的第二焦点,用F2表示。 F,到折射面顶点的距离称为第二焦距,用 表示。>0会聚作用、<0发散作用 将u=∞代入单球面折射 公式得 f, n,R n2-n1
第二焦距 n F2 f2 将u =∞代入单球面折射 公式得 与无穷远处物体所对应的像点,称为该折射面 的第二焦点,用F2表示。 F2到折射面顶点的距离称为第二焦距,用f2 表示。f2>0会聚作用、f2<0发散作用 R = − 2 2 2 1 n f n n

2、焦度: 决定折射面折射本领的量(n2~n1)/R称为折 射面的光焦度(或称为焦度)。用Φ表示 2 R 单位:屈光度D),1D=1/m1D=100度 Φ>0单球面折射系统具有会聚作用 Φ<0单球面折射系统具有发散作用 Φ值大,单球面折射系统会聚(发散)能力强 Φ值小,单球面折射系统会聚(发散)能力弱
2、焦度: n n 2 1 R − = 单位:屈光度(D),1D =1/m 1D=100度 决定折射面折射本领的量( n2 - n1 )/R 称为折 射面的光焦度(或称为焦度)。用φ表示 Φ>0 单球面折射系统具有会聚作用 Φ<0 单球面折射系统具有发散作用 |Φ|值大,单球面折射系统会聚(发散)能力强 |Φ|值小,单球面折射系统会聚(发散)能力弱

例1:某种液体(n=1.3)和玻璃 (n2=1.5)的分界面为球面。在液体 中有一物体放在这个折射球的主光轴 上离球面39cm处,并在球面前30cm处 成一虚像。求该折射球面的曲率半径, 并指出哪一种媒质处于球面的凹侧。 解: R n=1.3 n2=1.5 1.31.51.5-1.3 39-30R R=-12cm 11 液体处于折射面的凹侧
n n n n 1 2 2 1 U V R − 解: + = 1.3 1.5 1.5 1.3 39 30 R − + = − R cm = −12 液体处于折射面的凹侧 例1:某种液体(n1=1.3)和玻璃 (n2=1.5)的分界面为球面。在液体 中有一物体放在这个折射球的主光轴 上离球面39cm处,并在球面前30cm处 成一虚像。求该折射球面的曲率半径, 并指出哪一种媒质处于球面的凹侧。 O I P V u n1=1.3 n2=1.5

例2:圆柱形玻璃棒(n=1.5)的一端是 半径为2cm的凸球面。求:(1)当棒置于 空气中时,在棒的轴线上距离棒端外8cm 处的物点所成像的位置。(2)若将此棒 放入水(n=1.33)中时,物距不变, 像距应是多少(设棒足够长)?
例2:圆柱形玻璃棒(n=1.5)的一端是 半径为2cm的凸球面。求:(1)当棒置于 空气中时,在棒的轴线上距离棒端外8cm 处的物点所成像的位置。(2)若将此棒 放入水(n=1.33)中时,物距不变, 像距应是多少(设棒足够长)?

解:当棒置于空气中时,n11.0,n21.5,r=2cm, u=8cm,代入公式 11.51.5-1.0 得:v=12cm 为实像 2 当棒放入水中时,n11.33,n21.5,r=2cm,=8cm, 代入公式 1.33.1.51.5-1.33 得:v=-18.5cm,为虚 8 2 像,且像在棒外
解:当棒置于空气中时,n1=1.0,n2=1.5,r=2cm, u=8cm,代入公式 当棒放入水中时,n1=1.33,n2=1.5,r =2cm,u=8cm, 代入公式 得:v = -18.5 cm ,为虚 像,且像在棒外。 得:v = 12 cm 为实像 1.33 1.5 1.5 1.33 8 2 v − + = 1 1.5 1.5 1.0 8 2 v − + =