
74 翁译原理及实践 China-pub.co 下载 例如:Pascal的BNF以诸如 program -program-heading program-block. program-heading→. program-block→ 的文法规则开始(第1个规则认为程序由一个程序头、随后的分号、随后的程序块,以及位于 最后的一个句号组成)。在诸如C的带有独立编译的语言中,最普通的结构通常称作编译单元。 除非特别指出不是,在各种情况下都假定在文法规则中,第1个列出的就是这个最普通的结检 (在上下文无关文法的数学理论中,这个结构称作开始符号(start symbol)。 通过更深一些的术语可更清楚地区分结构名和字母表中的符号(因为它们经常是编译应用 程序的记号,所以我们一直调用记号符号)。由于在推导中必须被进一步替换(它们不终结推 导),所以结构名也称作非终结符(nonterminal)。相反地,由于字母表中的符号终结推导,所 以它们被称作终结符(terminal)。因为终结符通常是编译应用程序中的记号,所以这两个名字 在使用时是基本同义的。终结符和非终结符经常都被认作是符号 下面是一些由文法生成的语言示例。 例3.1考虑带有单个文法规则的文法G E-(E)a 这个文法有1个非终结符E、3个终结符()以及a。这个文法生成语言(G)={a,(a),(a), ((a)}={(a)|n是一个≥0的整型},即:串由零个或多个左括号、后接一个a,以及后面 是与左括号相同数量的右括号组成。作为这些串的一个推导示例,我们给出()的一个推导: E→(E)→(E)→(a) 例3.2考虑带有单个文法规则 E+(E) 的文法G。除了减少了洗项E·之外,这是与前例相同的文法。这个文法根本就不生成串,因 此它的语言是空的:L(G={}。其原因在于任何以E开头的推导都生成总是含有E的串,所以 没有办法推导出一个仅包含有终结符的串。实际上,与带有所有递归进程(如归纳论证或递归 函数)相同,递归地定义一个结构的文法规则必须总是有至少一个非递归情况(称之为基础情 况(base case)。本例中的文法并没有这样的情况,且任何潜在的推导都注定为无穷递归。 例3.3考虑带有单个文法规则 E-E+al a 的文法G。这个文法生成所有由若干个“+”分隔开的a组成的串 L(G)={a,a+a,a+a+a,a+a+a+a,... 为了(非正式地)查看它,可考虑规则E→E+a的效果:它引起串+a在推导右边不断地重复: EE+a→E+a+a→E+a+a+a→. 最后,必须用基础情况E一a来替换左边的E。 若要更正式一些,则可如下来归纳证明:首先,通过归纳a的数目来表示每个串a+a+ +a都在L(G中。推导E→a表示a在L(G)中:现在假设s=a+a++a在L(G中,且有m广1 个a,则存在推导E一*s。现在推导E一E+a一*s+a表示串s+a在L(G)中,且其中有n个a。 相反地,我们也表示出在L(G中的任何串s都必须属于格式a+a+ +a。这是通过归纳推导
例如:P a s c a l的B N F以诸如 p rogram → p rogram-heading ; p ro g r a m - b l o c k. p rogram-heading → . . . p rogram-block → . . . . . . 的文法规则开始(第 1个规则认为程序由一个程序头、随后的分号、随后的程序块,以及位于 最后的一个句号组成)。在诸如C的带有独立编译的语言中,最普通的结构通常称作编译单元。 除非特别指出不是,在各种情况下都假定在文法规则中,第 1个列出的就是这个最普通的结构 (在上下文无关文法的数学理论中,这个结构称作开始符号( start symbol))。 通过更深一些的术语可更清楚地区分结构名和字母表中的符号(因为它们经常是编译应用 程序的记号,所以我们一直调用记号符号)。由于在推导中必须被进一步替换(它们不终结推 导),所以结构名也称作非终结符(n o n t e r m i n a l)。相反地,由于字母表中的符号终结推导,所 以它们被称作终结符(t e r m i n a l)。因为终结符通常是编译应用程序中的记号,所以这两个名字 在使用时是基本同义的。终结符和非终结符经常都被认作是符号。 下面是一些由文法生成的语言示例。 例3.1 考虑带有单个文法规则的文法G E→(E)|a 这个文法有1个非终结符E、3个终结符(,) 以及a。这个文法生成语言 L(G) = {a, (a), ((a) ) , ( ( (a))),...} = {(n a) n | n 是一个≥0的整型 },即:串由零个或多个左括号、后接一个a,以及后面 是与左括号相同数量的右括号组成。作为这些串的一个推导示例,我们给出 ( (a) )的一个推导: E Þ (E) Þ ( (E)) Þ ( (a) ) 例3.2 考虑带有单个文法规则 E→(E) 的文法G。除了减少了选项E→a之外,这是与前例相同的文法。这个文法根本就不生成串,因 此它的语言是空的:L(G) = { }。其原因在于任何以E开头的推导都生成总是含有E的串,所以 没有办法推导出一个仅包含有终结符的串。实际上,与带有所有递归进程(如归纳论证或递归 函数)相同,递归地定义一个结构的文法规则必须总是有至少一个非递归情况(称之为基础情 况(base case))。本例中的文法并没有这样的情况,且任何潜在的推导都注定为无穷递归。 例3.3 考虑带有单个文法规则 E→E + a|a 的文法G。这个文法生成所有由若干个“+”分隔开的a 组成的串: L(G) = { a, a + a, a + a + a, a + a + a + a, . . . } 为了(非正式地)查看它,可考虑规则E→E + a 的效果:它引起串 + a 在推导右边不断地重复: E Þ E + a Þ E + a + a Þ E + a + a + a Þ . . . 最后,必须用基础情况E→a 来替换左边的E。 若要更正式一些,则可如下来归纳证明:首先,通过归纳 a 的数目来表示每个串a + a + . .. + a 都在L(G)中。推导E Þ a 表示a 在L(G) 中;现在假设s = a + a + ... + a 在L(G) 中,且有n-1 个a,则存在推导E Þ* s。现在推导E Þ E + a Þ *s + a 表示串s + a 在L(G)中,且其中有n 个a。 相反地,我们也表示出在L(G) 中的任何串s 都必须属于格式a + a + ... + a。这是通过归纳推导 7 4 编译原理及实践 下载

China-pub.Com 75 下载上 第3章上下文无关文法及分析 的长度得出的。假设推导的长度为1,则它属于格式E一,而且s是正确格式。现在假设以下 两个推导都为真:所有串都带有长度为一1的推导,并使E三*5是长度为n>1的推导:则这个 推导开头必须将E改为E+a,格式E三E+a三s'+a=s也是这样。则s'有长度为m1的推导, 格式a+a+…+a也是这样:因此,s本身必须也具有这个相同的格式。 例3.4考虑下面语句的极为简化的文法: statement if-stmt other if-simt-if (exp)statement i (exp)statemen else statement exn011 这个文法的语言包括位于类似C的格式中的嵌套i语句(我们已将逻辑测试表达式简化为0或1, 且除if语句外的所有语句都被放在终结符other中了)。例如,这个语言中的串是: 。ha e0 othe。 1Et1)。hex if 0 other else other if 1 other else other if 0 if 0 other if (0 if 1 other else other if 1 other else if 0 other else other 请注意,if语句中的可选else部分由用于if-stmt的文法规则中的单个选择指出。 在前面我们已注意到:BNF中的文法规则规定了并置和选择,但不具有与正则表达式的 相等同的特定重复运算。由于可由递归得到重复,所以这样的运算实际并不必要(如同在功能 语言中的程序员所知道的)。例如,文法规则 A-Aala 或文法规则 A→aAla 都生成语言{aIn是≥1的整型}(具有1个或多个a的所有串的集合),该语言与由正则表达式 a+生成的语言相同。例如,串aaaa可由带有推导 A→Aa→Aaa→Aaaa=aaaa 的第1个文法规则生成。一个类似的推导在第2个文法规则中起作用。由于非终结符A作为定义 A的规则左边的第1个符号出现,所以这些文法中的第1个是左递归(left recursive)9,第2个文 法则是右递归(right recursive).。 例33是左递归文法规则的另一个示例,它引出串“+”的重复。可将本例及前一个示例 归纳如下。考虑一个规则形式 A-AdB 其中a和B代表任意串,且B不以4开头。这个规则生成形式B、Ba、Baa、Baaa、的所有 串(所有串均以B开头,其后是零个或多个()。因此,这个文法规则在效果上与正则表达式 Bα*相同。类似地,右递归文法规则 A→a4IB 日这是左递归中的特珠情况,称作直接左递归(immediate).下一章将讨论一些更普通的情况
的长度得出的。假设推导的长度为1,则它属于格式E Þ a,而且s 是正确格式。现在假设以下 两个推导都为真:所有串都带有长度为 n-1的推导,并使E Þ* s 是长度为n > 1的推导;则这个 推导开头必须将E改为E +a,格式E Þ E + a Þ*s’ + a = s 也是这样。则s’有长度为n-1的推导, 格式a + a + ... + a 也是这样;因此,s 本身必须也具有这个相同的格式。 例3.4 考虑下面语句的极为简化的文法: statement → if-stmt | o t h e r if-stmt → if (e x p) s t a t e m e n t | if (e x p) statement e l s e s t a t e m e n t exp → 0 | 1 这个文法的语言包括位于类似 C的格式中的嵌套i f语句(我们已将逻辑测试表达式简化为 0或1, 且除i f语句外的所有语句都被放在终结符o t h e r中了)。例如,这个语言中的串是: o t h e r if ( 0 ) other if ( 1 ) other if ( 0 ) other else other if ( 1 ) other else other if ( 0 ) if ( 0 ) other if ( 0 ) if ( 1 ) other else other if ( 1 ) other else if ( 0 ) other else other . . . 请注意,if 语句中的可选else 部分由用于if-stmt 的文法规则中的单个选择指出。 在前面我们已注意到: B N F中的文法规则规定了并置和选择,但不具有与正则表达式的 * 相等同的特定重复运算。由于可由递归得到重复,所以这样的运算实际并不必要(如同在功能 语言中的程序员所知道的)。例如,文法规则 A → Aa | a 或文法规则 A → aA | a 都生成语言{a n | n 是≥1的整型}(具有1个或多个a 的所有串的集合),该语言与由正则表达式 a +生成的语言相同。例如,串aaaa 可由带有推导 A Þ Aa Þ Aaa Þ Aaaa Þ a a a a 的第1个文法规则生成。一个类似的推导在第 2个文法规则中起作用。由于非终结符 A作为定义 A的规则左边的第1个符号出现,所以这些文法中的第1个是左递归(left recursive) ,第2个文 法则是右递归(right recursive)。 例3 . 3是左递归文法规则的另一个示例,它引出串“ +a”的重复。可将本例及前一个示例 归纳如下。考虑一个规则形式 A→Aa|b 其中a 和b 代表任意串,且b 不以A开头。这个规则生成形式b、b a、b a a、b a a a、. . . .. . .的所有 串(所有串均以 b开头,其后是零个或多个 a)。因此,这个文法规则在效果上与正则表达式 b a*相同。类似地,右递归文法规则 A→aA|b 第 3章 上下文无关文法及分析 7 5 下载 这是左递归中的特殊情况,称作直接左递归( immediate left recursion),下一章将讨论一些更普通的情况

76 翁译原理及实践 China-pub.C 下载 (其中B并不在A处结束)生成所有串B、a邱、a邱、aa邓、 如果要编写生成与正则表达式a*相同语言的文法,则文法规则必须有一个用于生成空串 的的表示法(因为正则表达式ā*匹配空串)。这样的文法规则的右边必须为空,可在右边什么 也不写,如在 empry 中,但大多数情况都使用ε元符号表示空串(与在正则表达式中的用法类似): emp→e 这样的文法规则称作g-产生式(e-production)。生成包括了空串的文法必须至少有一个e-产 生式。 现在可以将一个与正则表达式a*相等的文法写作 A-Aa|ε 或 A-aA 8 两个文法都生成语言{a|n是≥0的整型}=L(a*)。-产生式在定义可选的结构时也很有 用,我们马上就能看到这一点。 下面用更多的一些示例来小结这个部分。 例3.5考虑文法 A→(A)AIE 这个文法生成所有“配对的括号”的串。例如,串()())()就由下面的推导生成(利用ε-产 生式去除无用的A): A=(A)A=(A)(A)A三(A)(A)三(A)()三(A)A)() ()A)()=()(A)A)()=()(A》() 三()(A)A》()=())A》()三)()》() 例3.6例3.4中的语句文法用e-产生式还可写作: statement-ifstmt l other if-stmtif exp)statement else-part else-part else statement e ep011 请注意,e-产生式指出结构else parti是可选的。 例3.7考虑一个语句序列的以下文法G: stmt-sequencestmt;stmt-sequence stmt stmt -s 这个文法生成由分号分隔开的一个或多个语句序列(语句已被提练到单个终结符s中了): L(G)={s,8;3,s;s:s,..} 如要允许语句序列也可为空,则可写出以下的文法G: stmt-sequencestmt;stmt-sequence stmte 但是它将分号变为一个语句结束符号(terminator)而不是分隔符(separator): L(G)={E,s;,s:s;,s:s:s:,..1
(其中b并不在A处结束)生成所有串b、a b、a a b、a aab、. . . . . . 如果要编写生成与正则表达式 a *相同语言的文法,则文法规则必须有一个用于生成空串 的的表示法(因为正则表达式 a *匹配空串)。这样的文法规则的右边必须为空,可在右边什么 也不写,如在 empty → 中,但大多数情况都使用 元符号表示空串(与在正则表达式中的用法类似): empty → 这样的文法规则称作 - 产生式( -p r o d u c t i o n)。生成包括了空串的文法必须至少有一个 -产 生式。 现在可以将一个与正则表达式a *相等的文法写作 A→A a| 或 A→a A| 两个文法都生成语言{a n | n 是≥0的整型} = L (a *)。 -产生式在定义可选的结构时也很有 用,我们马上就能看到这一点。 下面用更多的一些示例来小结这个部分。 例3.5 考虑文法 A→ (A) A| 这个文法生成所有“配对的括号”的串。例如,串 (( ) (( ))) ( )就由下面的推导生成(利用 -产 生式去除无用的A): A Þ ( A ) A Þ ( A ) ( A ) A Þ ( A ) ( A ) Þ ( A ) ( ) Þ (( A ) A ) ( ) Þ (( ) A ) ( ) Þ (( ) ( A ) A ) ( ) Þ (( ) ( A )) ( ) Þ (( ) (( A ) A )) ( ) Þ (( ) (( ) A )) ( ) Þ (( ) (( ))) ( ) 例3.6 例3 . 4中的语句文法用 -产生式还可写作: statement → if-stmt | o t h e r if-stmt → if ( e x p ) statement else-part e l s e - p a rt → else statement | exp → 0 | 1 请注意, -产生式指出结构else part是可选的。 例3.7 考虑一个语句序列的以下文法G: stmt-sequence → stmt ; s t m t - s e q u e n c e | s t m t stmt → s 这个文法生成由分号分隔开的一个或多个语句序列(语句已被提练到单个终结符 s中了): L(G) = { s, s;s, s;s;s, ...} 如要允许语句序列也可为空,则可写出以下的文法 G’: stmt-sequence → stmt ; stmt-sequence | stmt → s 但是它将分号变为一个语句结束符号(t e r m i n a t o r)而不是分隔符(s e p a r a t o r): L(G’) = { , s;, s;s;, s;s;s;, ...} 7 6 编译原理及实践 下载

China-pub.com 下载H 第3章上下文无关文法及分析 77 如果允许语句序列可为空,但仍要求保留分号作为语句分隔符,则须将文法写作: stmt-sequence nonempty-stmt-sequence nonempty-stmt-sequence-stmt:nonempty-stmt-sequence simt stt→s 这个例子说明在构造可选结构时,必须留意e-产生式的位置。 3.3分析树与抽象语法树 3.3.1分析树 推导为构造来自一个初始的非终结符的特定终结符的串提供了一个办法,但是推导并未唯 一地表示出它们所构造的结构。总而言之,对于同一个串可有多个推导。例如,使用图31中 的推导从简单表达式文法构造出记号串 n number) 图3-2给出了这个串的另一个推导。二者唯一的差别在于提供的替换顺序,而这其实是一 个很表面的差别。为了把它表示得更清楚一些,我们需要表示出终结符串的结构,而这些终结 符将推导的主要特征抽取出来,同时却将表面的差别按顺序分解开来。这样的表示法就是树结 构,它称作分析树。 (1)eD→exp op exp 【ep+exp op exp 2) →(ep)opep [ep→(ep)] 3 →(exp op exp)pep 【ep+exp op exp ber op exp) op exp ep→umber] exp)op exp [op→-】 (6 →number-number)pep [ep→number】 (7) →(number-number)texp [op-+】 (8) (number-number)*number 【ep→number] 图3-2表达式34-3)42的另一个推导 与推导相对应的分析树(parse tree)是一个作了标记的树,其中内部的节点由非终结符标 出,树叶节点由终结符标出,每个内部节点的子节点都表示推导的一个步骤中的相关非终结符 的替换。 以下是一个简单的示例,推导: ep exp op exp →number op exp →number+ep number+number 与分析树
如果允许语句序列可为空,但仍要求保留分号作为语句分隔符,则须将文法写作: stmt-sequence → nonempty-stmt-sequence | nonempty-stmt-sequence → stmt ; nonempty-stmt-sequence | s t m t stmt → s 这个例子说明在构造可选结构时,必须留意 - 产生式的位置。 3.3 分析树与抽象语法树 3.3.1 分析树 推导为构造来自一个初始的非终结符的特定终结符的串提供了一个办法,但是推导并未唯 一地表示出它们所构造的结构。总而言之,对于同一个串可有多个推导。例如,使用图 3 - 1中 的推导从简单表达式文法构造出记号串 ( number - number ) * n u m b e r 图3 - 2给出了这个串的另一个推导。二者唯一的差别在于提供的替换顺序,而这其实是一 个很表面的差别。为了把它表示得更清楚一些,我们需要表示出终结符串的结构,而这些终结 符将推导的主要特征抽取出来,同时却将表面的差别按顺序分解开来。这样的表示法就是树结 构,它称作分析树。 图3-2 表达式( 3 4 - 3 ) * 4 2 的另一个推导 与推导相对应的分析树(parse tree)是一个作了标记的树,其中内部的节点由非终结符标 出,树叶节点由终结符标出,每个内部节点的子节点都表示推导的一个步骤中的相关非终结符 的替换。 以下是一个简单的示例,推导: e x p Þ exp op exp Þ number op exp Þ number + e x p Þ number + n u m b e r 与分析树 第 3章 上下文无关文法及分析 7 7 下载
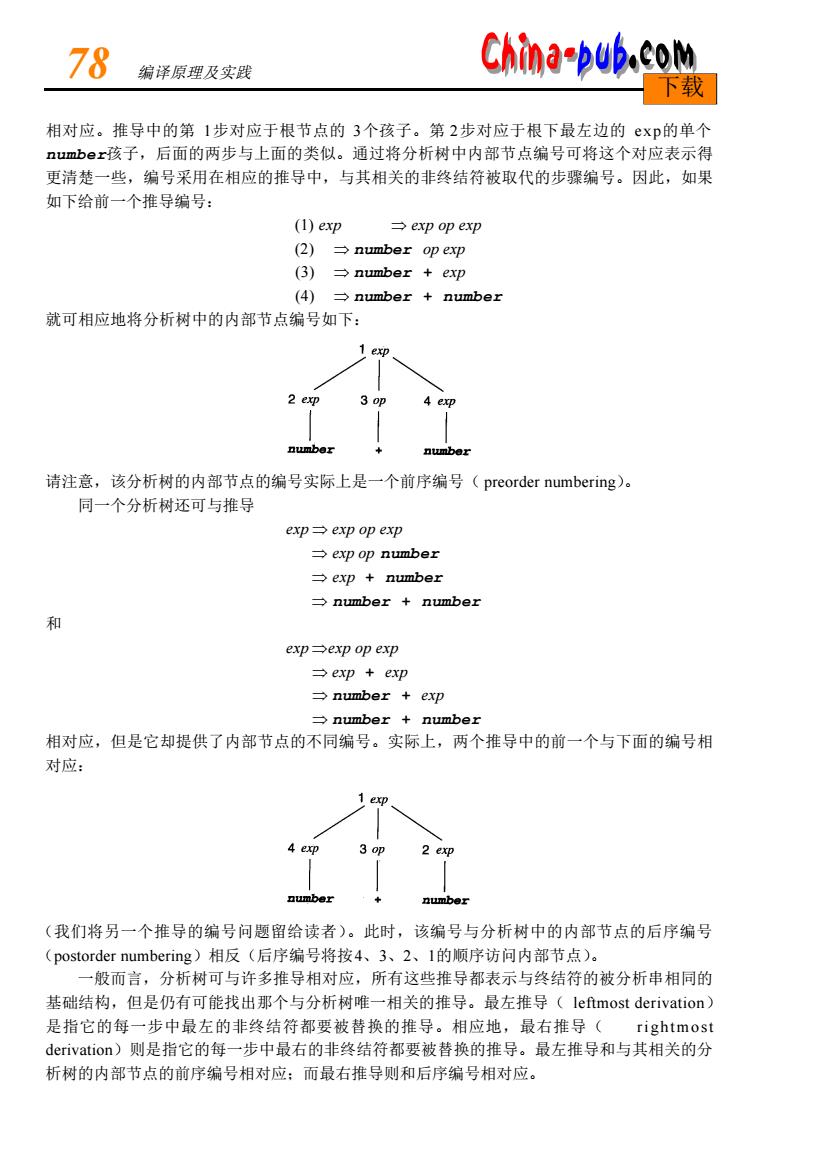
78 翁译原理及实践 China-pub.co 下载 相对应。推导中的第1步对应于根节点的3个孩子。第2步对应于根下最左边的exp的单个 umberi孩子,后面的两步与上面的类似。通过将分析树中内部节点编号可将这个对应表示得 更清楚一些,编号采用在相应的推导中,与其相关的非终结符被取代的步骤编号。因此,如果 如下给前一个推导编号: (1)exp →exp op exp (2)number op exp (3)→number+exp (4)→number+number 就可相应地将分析树中的内部节点编号如下: 请注意,该分析树的内部节点的编号实际上是一个前序编号(preorder numbering): 同一个分析树还可与推导 ep→exp op exp →exp op number →exp+number →number+number 布 expexp op exp →exp+exp number exp mber n mbe: 相对应,但是它却提供了内部节点的不同编号。实际上,两个推导中的前一个与下面的编号相 对应: (我们将另一个推导的编号问题留给读者)。此时,该编号与分析树中的内部节点的后序编号 (postorder numbering)相反(后序编号将按4、3、2、1的顺序访问内部节点)。 般而言,分析树可与许多推导相对应,所有这些推导都表示与终结符的被分析串相同的 基础结构,但是仍有可能找出那个与分析树唯一相关的推导。最左推导(leftmost derivation) 是指它的每一步中最左的非终结符都要被替换的推导。相应地,最右推导( rightmos derivation)则是指它的每一步中最右的非终结符都要被替换的推导。最左推导和与其相关的分 析树的内部节点的前序编号相对应:而最右推导则和后序编号相对应
相对应。推导中的第 1步对应于根节点的 3个孩子。第 2步对应于根下最左边的 e x p的单个 n u m b e r孩子,后面的两步与上面的类似。通过将分析树中内部节点编号可将这个对应表示得 更清楚一些,编号采用在相应的推导中,与其相关的非终结符被取代的步骤编号。因此,如果 如下给前一个推导编号: (1) e x p Þ exp op exp ( 2 ) Þ number op exp ( 3 ) Þ number + e x p ( 4 ) Þ number + n u m b e r 就可相应地将分析树中的内部节点编号如下: 请注意,该分析树的内部节点的编号实际上是一个前序编号( preorder numbering)。 同一个分析树还可与推导 e x p Þ exp op exp Þ exp op n u m b e r Þ e x p + number Þ number + n u m b e r 和 e x p Þexp op exp Þ e x p + e x p Þ number + e x p Þ number + n u m b e r 相对应,但是它却提供了内部节点的不同编号。实际上,两个推导中的前一个与下面的编号相 对应: (我们将另一个推导的编号问题留给读者)。此时,该编号与分析树中的内部节点的后序编号 (postorder numbering)相反(后序编号将按4、3、2、1的顺序访问内部节点)。 一般而言,分析树可与许多推导相对应,所有这些推导都表示与终结符的被分析串相同的 基础结构,但是仍有可能找出那个与分析树唯一相关的推导。最左推导( leftmost derivation) 是指它的每一步中最左的非终结符都要被替换的推导。相应地,最右推导( r i g h t m o s t d e r i v a t i o n)则是指它的每一步中最右的非终结符都要被替换的推导。最左推导和与其相关的分 析树的内部节点的前序编号相对应;而最右推导则和后序编号相对应。 7 8 编译原理及实践 下载