
1844 The Journal of Finance amines time variation in overconfidence to derive implications about the signs of short-term versus long-term return autocorrelations.Section IV con- cludes by summarizing our findings,relating our analysis to the literature on exogenous noise trading,and discussing issues related to the survival of overconfident traders in financial markets. I.Overconfidence and Biased Self-Attribution Our theory relies on two psychological regularities:overconfidence and attribution bias.In their summary of the microfoundations of behavioral finance,DeBondt and Thaler (1995)state that "perhaps the most robust finding in the psychology of judgment is that people are overconfident."Ev- idence of overconfidence has been found in several contexts.Examples in- clude psychologists,physicians and nurses,engineers,attorneys,negotiators, entrepreneurs,managers,investment bankers,and market professionals such as security analysts and economic forecasters.2Further,some evidence sug- gests that experts tend to be more overconfident than relatively inexperi- enced individuals (Griffin and Tversky (1992)).Psychological evidence also indicates that overconfidence is more severe for diffuse tasks (e.g.,making diagnoses of illnesses),which require judgment,than for mechanical tasks (e.g.,solving arithmetic problems);and more severe for tasks with delayed feedback as opposed to tasks that provide immediate and conclusive outcome feedback (see Einhorn (1980)).Fundamental valuation of securities (fore- casting long-term cash flows)requires judgment about open-ended issues, and feedback is noisy and deferred.We therefore focus on the implications of overconfidence for financial markets.3 Our theory assumes that investors view themselves as more able to value securities than they actually are,so that they underestimate their forecast error variance.This is consistent with evidence that people overestimate their own abilities,and perceive them- selves more favorably than they are viewed by others. Several experimental studies find that individuals underestimate their error variance in making predictions,and overweight their own forecasts relative to those of others.5 The second aspect of our theory is biased self-attribution:The confidence of the investor in our model grows when public information is in agreement with his information,but it does not fall commensurately when public information 2 See respectively:Oskamp (1965);Christensen-Szalanski and Bushyhead,(1981),Bau- mann,Deber,Thompson,(1991);(Kidd (1970);Wagenaar and Keren(1986);Neale and Bazer- man (1990);Cooper,Woo,and Dunkelberg (1988);Russo and Schoemaker (1992);Vonholstein (1972);Ahlers and Lakonishok (1983),Elton,Gruber,and Gultekin (1984),Froot and Frankel (1989),DeBondt and Thaler (1990),DeBondt (1991).See Odean(1998)for a good summary of empirical research on overconfidence. Odean (1998)(Sec.II.D)also makes a good argument for why overconfidence should dom- inate in financial markets.Also,Bernardo and Welch(1998)offer an evolutionary explanation for why individuals should be overconfident. 4 Greenwald (1980),Svenson (1981),Cooper et al.1988,and Taylor and Brown (1988). 5 See Alpert and Raiffa(1982),Fischhoff,Slovic,and Lichtenstein(1977),Batchelor and Dua (1992),and the discussions of Lichtenstein,Fischhoff,and Phillips(1982)and Yates(1990)

Investor Psychology and Market Reactions 1845 contradicts his private information.The psychological evidence indicates that people tend to credit themselves for past success,and blame external factors for failure (Fischhoff(1982),Langer and Roth(1975),Miller and Ross(1975), Taylor and Brown(1988)).As Langer and Roth(1975)put it,"Heads I win,tails it's chance";see also the discussion of De Long et al.(1991). II.The Basic Model:Constant Confidence This section develops the model with static confidence.Section III consid- ers time-varying confidence.Each member of a continuous mass of agents is overconfident in the sense that if he receives a signal,he overestimates its precision.We refer to those who receive the signal as the informed,I,and those who do not as the uninformed,U.For tractability,we assume that the informed are risk neutral and that the uninformed are risk averse. Each individual is endowed with a basket containing security shares,and a risk-free numeraire that is a claim to one unit of terminal-period wealth There are four dates.At date 0,individuals begin with their endowments and identical prior beliefs,and trade solely for optimal risk-transfer pur- poses.At date 1,I receives a common noisy private signal about underlying security value and trades with U.At date 2,a noisy public signal arrives, and further trade occurs.At date 3,conclusive public information arrives, the security pays a liquidating dividend,and consumption occurs.All ran- dom variables are independent and normally distributed. The risky security generates a terminal value of 0,which is assumed to be normally distributed with mean and variance o.For most of the paper we set 0=0 without loss of generality.The private information signal received by I at date 1 is S1=0+∈, (1) where e~N(0,2)(so the signal precision is 1/02).U correctly assesses the error variance,but I underestimates it to be o<o2.The differing beliefs about the noise variance are common knowledge to all.?Similarly,the date 2 public signal is S2=0+7, (2) 6 Some previous models with common private signals include Grossman and Stiglitz(1980), Admati and Pfleiderer(1988),and Hirshleifer et al.(1994).If some analysts and investors use the same information sources to assess security values,and interpret them in similar ways,the error terms in their signals will be correlated.For simplicity,we assume this correlation is unity;how- ever,similar results would obtain under imperfect(but nonzero)correlation in signal noise terms. 7 It is not crucial for the analysis that the uninformed correctly assesses the private signal variance,only that he does not underestimate it as much as the informed does.Also,because U does not possess a signal to be overconfident about,he could alternatively be interpreted as a fully rational trader who trades to exploit market mispricing.Furthermore,most of the results will obtain even if investors are symmetrical both in their overconfidence and their signals. Results similar to those we derive would apply in a setting where identical overconfident in- dividuals receive correlated private signals

1846 The Journal of Finance where the noise term n-N(0,p)is independent of 0 and e.Its variance op is correctly estimated by all investors. Our simplifying assumption that all private information precedes all pub- lic information is not needed for the model's implications.It is essential that at least some noisy public information arrives after a private signal.The model's implications stand if,more realistically,additional public informa- tion precedes or is contemporaneous with the private signal. The formal role of the uninformed in this paper is minimal because prices are set by the risk-neutral informed traders.The rationale for the assump- tion of overconfidence is that the investor has a personal attachment to his own signal.This implies some other set of investors who do not receive the same signal.Also,similar results will hold if both groups of investors are risk averse,so that both groups influence price.We have verified this ana- lytically in a simplified version of the model.So long as the uninformed are not risk-neutral price setters,the overconfident informed will push price away from fully rational values in the direction described here. A.Equilibrium Prices and Trades Because the informed traders are risk neutral,prices at each date satisfy P1=Ec[00+e] (3) P2=Ec[00+∈,0+n], (4) where the subscript C denotes the fact that the expectation operator is cal- culated based on the informed traders'confident beliefs.Trivially,Pa=6.By standard properties of normal variables (Anderson (1984),Chap.2), P1= 02 (0+e) (5) 子+8 B=io哈+哈g+听吃。ui呢 -0+ De+、 D, (6) D where D≡o(o呢+o)+o尼c2 B.Implications for Price Behavior This section examines the implications of static confidence for over-and underreactions to information and empirical securities returns patterns.Sub- section B.1 examines price reactions to public and private information,sub- section B.2 examines the implications for price-change autocorrelations,and subsection B.3 examines implications for event-studies.Subsection B.4 dis- cusses some as-yet-untested empirical implications of the model
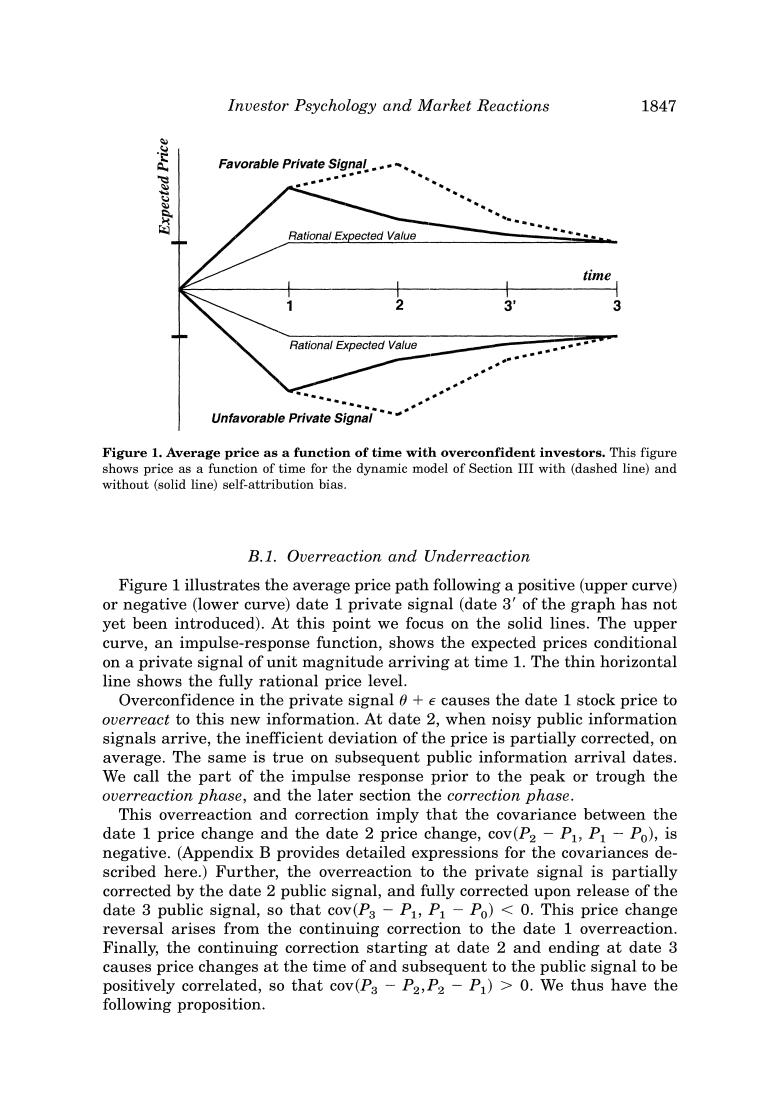
Investor Psychology and Market Reactions 1847 Favorable Private Signal Rational Expected Value time Rational Expected Value Unfavorable Private Signal Figure 1.Average price as a function of time with overconfident investors.This figure shows price as a function of time for the dynamic model of Section III with(dashed line)and without (solid line)self-attribution bias. B.1.Overreaction and Underreaction Figure 1 illustrates the average price path following a positive(upper curve) or negative (lower curve)date 1 private signal(date 3'of the graph has not yet been introduced).At this point we focus on the solid lines.The upper curve,an impulse-response function,shows the expected prices conditional on a private signal of unit magnitude arriving at time 1.The thin horizontal line shows the fully rational price level. Overconfidence in the private signal +e causes the date 1 stock price to overreact to this new information.At date 2,when noisy public information signals arrive,the inefficient deviation of the price is partially corrected,on average.The same is true on subsequent public information arrival dates. We call the part of the impulse response prior to the peak or trough the overreaction phase,and the later section the correction phase. This overreaction and correction imply that the covariance between the date 1 price change and the date 2 price change,cov(P2-P1,P1-Po),is negative.(Appendix B provides detailed expressions for the covariances de- scribed here.)Further,the overreaction to the private signal is partially corrected by the date 2 public signal,and fully corrected upon release of the date 3 public signal,so that cov(Ps-P1,P1-Po)<0.This price change reversal arises from the continuing correction to the date 1 overreaction. Finally,the continuing correction starting at date 2 and ending at date 3 causes price changes at the time of and subsequent to the public signal to be positively correlated,so that cov(Pa-P2,P2-P1)>0.We thus have the following proposition

1848 The Journal of Finance PROPOSITION 1:If investors are overconfident,then: 1.Price moves resulting from private information arrival are on average partially reversed in the long run. 2.Price moves in reaction to the arrival of public information are posi- tively correlated with later price changes. The pattern of correlations described in Proposition 1 is potentially testable by examining whether long-run reversals following days with public news events are smaller than reversals on days without such events.The price behavior around public announcements has implications for corporate event studies (see Subsection B.3). B.2.Unconditional Serial Correlations and Volatility Return autocorrelations in well-known studies of momentum and reversal are calculated without conditioning on the arrival of a public information signal.To calculate a return autocorrelation that does not condition on whether private versus public information has arrived,consider an experiment where the econometrician randomly picks consecutive dates for price changes(dates 1 and 2,versus dates 2 and 3).The date 2 and 3 price changes are positively correlated,but the date 1 and 2 price changes are negatively correlated. Suppose that the econometrician is equally likely to pick either pair of con- secutive dates.Then the overall autocorrelation is negative. PROPOSITION 2:If investors are overconfident,price changes are uncondition- ally negatively autocorrelated at both short and long lags. Thus,the constant-confidence model accords with long-run reversals(nega- tive long-lag autocorrelations)but not with short-term momentum(positive short-lag autocorrelation).However,the short-lag autocorrelation will be pos- itive in a setting where the extremum in the impulse response function is sufficiently smooth,because the negative autocovariance of price changes surrounding a smooth extremum will be low in absolute terms.Such a set- ting,based on biased self-attribution and outcome-dependent confidence,is considered in Section III. Overconfidence causes wider swings at date 1 away from fundamentals, thereby causing excess price volatility around private signals(var(PI-Po)), as in Odean(1998).Greater overconfidence also causes relative underweight- ing of the public signal,which tends to reduce date 2 variance.However,the wide date 1 swings create a greater need for corrective price moves at dates 2 and 3,so that greater overconfidence can either decrease or increase the volatility around public signals(var(P2-P)).(Explicit expressions for the variances of this section are contained in Appendix B.)Consider again an econometrician who does not condition on the occurrence of private or public news arrival.When calculating price change variances he gives equal weight to price changes P1-Po,P2-P1,and Ps-P2.The unconditional volatility