
NMR信号的检测 ■ 为了研究磁化矢量M发生的变化,在与B。 垂直的平面内施以频率为®,的交变磁场: B =2B cos@ot 设其方向与X轴相同。 ■ 此时核磁矩既绕B,进动,一又绕B进动;或 者认为核磁矩绕B,与B的合成矢量进动。 ■ 矢量M偏离M,方向,而在Xy平面产生分 量
NMR信号的检测 ◼ 为了研究磁化矢量M发生的变化,在与 垂直的平面内施以频率为 的交变磁场: 设其方向与x轴相同。 ◼ 此时核磁矩既绕 进动,又绕 进动;或 者认为核磁矩绕 与 的合成矢量进动。 ◼ 矢量M偏离 方向,而在x-y平面产生分 量 1 1 0 B B t = 2 cos B0 0 B0 B1 B0 B1 M xy

NMR信号的检测 ■将交变磁场B=2Bcos®1分解成以相同的 角频率但作相反方向旋转的两旋转的两 旋转磁场之和,即: B,=B*+B=B,eo°+Be,0 式中,B=BQ为以o的角频率按逆时针 旋转的磁场;B=Beo为以相同的角频率 ®按顺时针旋转的磁场
NMR信号的检测 ◼ 将交变磁场 分解成以相同的 角频率 但作相反方向旋转的两旋转的两 旋转磁场之和,即: 式中, 为以 的角频率按逆时针 旋转的磁场; 为以相同的角频率 按顺时针旋转的磁场。 1 1 0 B B t = 2 cos 0 0 1 1 1 1 1 i i B B B B e B e + − − = + = + 0 1 1 i B B e + = 0 1 1 i B B e − − = 0 0 0

NMR信号的检测 ■ 引入以的角速度与B同步方向旋转的旋 转坐标系。由于对系统的能量不起影响, 故在旋转坐标系中有两个“静磁 场”(围。B)作用着。B的相位是随机的, 一般令其与-轴同向。这样,磁化矢量M 将绕“静磁场”选动。进动频率为 @=-YB
NMR信号的检测 ◼ 引入以 的角速度与 同步方向旋转的旋 转坐标系。由于 对系统的能量不起影响, 故在旋转坐标系中有两个“静磁 场”(即 , )作用着。 的相位是随机的, 一般令其与 -轴同向。这样,磁化矢量M 将绕“静磁场” 进动。进动频率为 0 B1 − B1 + B0 B1 − B1 − ' x B1 − 1 1 B − = −

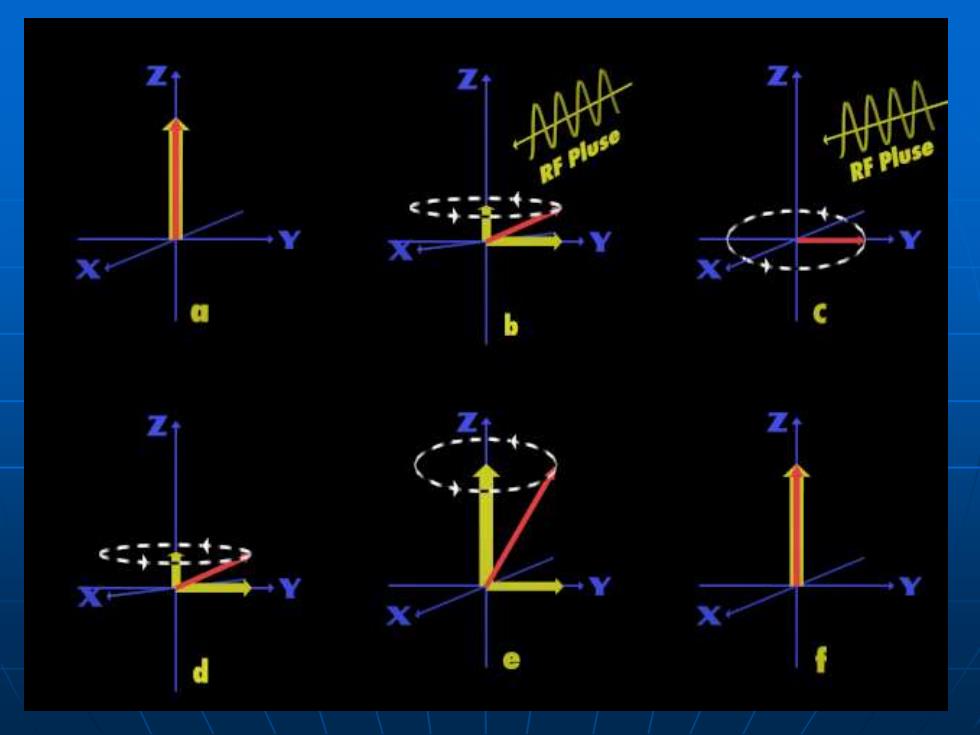
NMR信号的检测 ■当外施交变磁场经过时间后,磁化矢量M处于 B=O,t。此时在X-y平面上有分量M,=Msm0 M”的形成可以看作是由原先相位均匀分布的核磁 矩向某一方句集中而使矢量加强的结果。 ■M,在固定坐标系中,以@0的角速度绕Z轴在X=y平 面内旋转。若在该平面内置一检测线圈,则M,将 以每秒⊙/2π的频率切割线圈,从而产生电势。这 就是检测到的NMR信号
NMR信号的检测 ◼ 当外施交变磁场经过时间t后,磁化矢量M处于 。此时在x-y平面上有分量 。 的形成可以看作是由原先相位均匀分布的核磁 矩向某一方向集中而使矢量加强的结果。 ◼ 在固定坐标系中,以 的角速度绕z轴在x-y平 面内旋转。若在该平面内置一检测线圈,则 将 以每秒 的频率切割线圈,从而产生电势。这 就是检测到的NMR信号。 sin = 1 t M M xy = M xy 0 M xy M xy 0 / 2
RF Pluse RF Pluse