
定积分及其应用 圆柱 环形圆柱 圆锥 圆台 球体 1 V=πr2h 4 V= V=3m3 V=π(R-r)2h V= 3π(R2+Rr+r2)h
圆柱 环形圆柱 圆锥 圆台 球体 𝑉 = 𝜋𝑟 2ℎ 𝑉 = 𝜋(𝑅 − 𝑟) 2ℎ 𝑉 = 1 3 𝜋𝑟 2ℎ 𝑉 = 1 3 𝜋(𝑅 2+𝑅𝑟 + 𝑟 2 )ℎ 𝑉 = 4 3 𝜋𝑟 3

定积分及其应用 旋转体的特点 1.在区间D上,旋转体的体积具有对区间的可加性. 2.任何一个垂直于旋转轴的平面截旋转体所得的截口图形均为圆. f() X
旋转体的特点 1.在区间D上,旋转体的体积具有对区间的可加性. 2.任何一个垂直于旋转轴的平面截旋转体所得的截口图形均为圆. O a b x y y=f (x)
定积分及其应用 一般地,如果旋转体由连续曲线y=f(x)、直线x=a、a=b及x 轴所围成的曲边梯形绕x轴旋转一周而成的立体,体积多少? 1如图所示,x为积分变量,区间为[a,b.y 、B 2.在[a,b]上任取一个小区间[x,x+dx] A y=f(x) 则此小区间上的小曲边体形绕x轴旋转 而成的薄片的体积微元为 dV=π[f(x)]2dx 3.在[a,b]上写出定积分表达式为 v=πfo]2dx
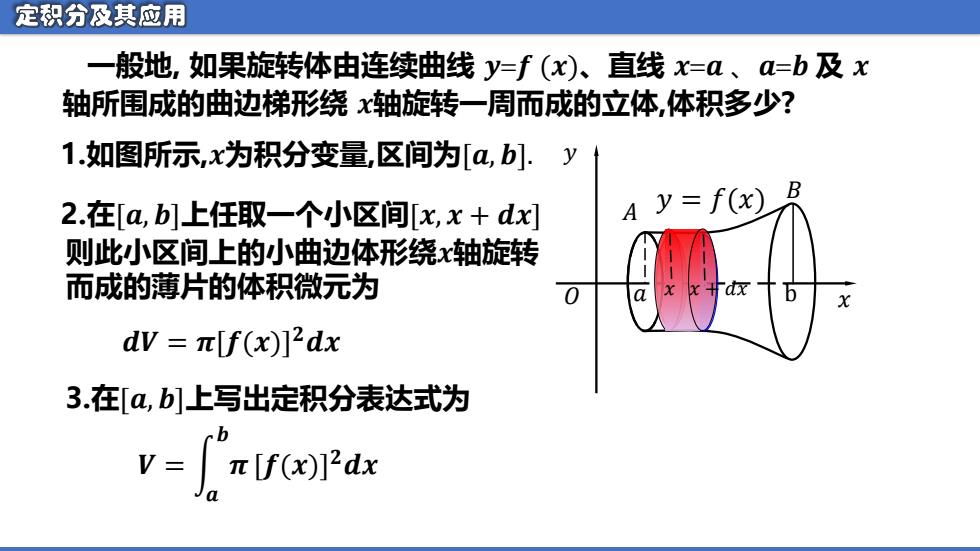
一般地, 如果旋转体由连续曲线 𝒚=𝒇 (𝒙)、直线 𝒙=𝒂 、𝒂=𝒃 及 𝒙 轴所围成的曲边梯形绕 𝒙轴旋转一周而成的立体,体积多少? 1.如图所示,𝒙为积分变量,区间为[𝒂, 𝒃]. 2.在[𝒂, 𝒃]上任取一个小区间[𝒙, 𝒙 + 𝒅𝒙] 则此小区间上的小曲边体形绕𝒙轴旋转 而成的薄片的体积微元为 3.在[𝒂, 𝒃]上写出定积分表达式为 𝑎 𝑥 b 𝑥 𝑦 𝑥 + 𝑑𝑥 𝐵 𝐴 𝑂 𝑦 = 𝑓(𝑥) 𝒅𝑽 = 𝝅[𝒇(𝒙)] 𝟐𝒅𝒙 𝑽 = න 𝒂 𝒃 𝝅[𝒇(𝒙)] 𝟐𝒅𝒙