
第三讲要素禀赋论 赫克歇尔一俄林理论(H-O定理) 假设条件 H-O理论内容 H-0-S定理(要素均等化定理 理论验证,里昂剔夫之谜 特定要素模型 计在价質
1 第三讲 要素禀赋论 z 赫克歇尔—俄林理论(H-O定理) z 假设条件 z H-O理论内容 z H-O-S定理(要素均等化定理) z 理论验证,里昂剔夫之谜 z 特定要素模型

假设条件 2×2×2模型,两国家,两产品,两要素 产品生产函数相同,技术水平一样,规 模报酬不变 偏好相同 产品的要素密集度不同 完全竞争,无任何贸易障碍 要素在一国内自由流动,国际间不流动 资源被充分利用 计在价質
2 一、假设条件 z 2 × 2 × 2模型,两国家,两产品,两要素 z 产品生产函数相同,技术水平一样,规 模报酬不变 z 偏好相同 z 产品的要素密集度不同 z 完全竞争,无任何贸易障碍 z 要素在一国内自由流动,国际间不流动, 资源被充分利用

国家的要素丰裕度 可利用的资本总量和可利用的劳动总量 之比 (KL)1←(KL)2表明国家1为劳动丰裕国 要素的价格之比 (wr)1≤(wr)2表明国家1为劳动丰裕国 计至价質
3 国家的要素丰裕度 国家的要素丰裕度 z 可利用的资本总量和可利用的劳动总量 之比 z (K/L) 1<(K/L)2 表明国家 1为劳动丰裕国 z 要素的价格之比 z (w/r ) 1<(w/r) 2表明国家 1为劳动丰裕国

产品的要素密集度 最优要素组合时的 K 资本投入量和劳动 投入量之比 最优要素组合的点 位于原点发出的一 X 条射线上,其斜率 代表该产品的要素 密集度 计价質
4 产品的要素密集度 产品的要素密集度 z 最优要素组合时的 资本投入量和劳动 投入量之比 z 最优要素组合的点 位于原点发出的一 条射线上,其斜率 代表该产品的要素 密集度 K KY K Y X X L Y L L X
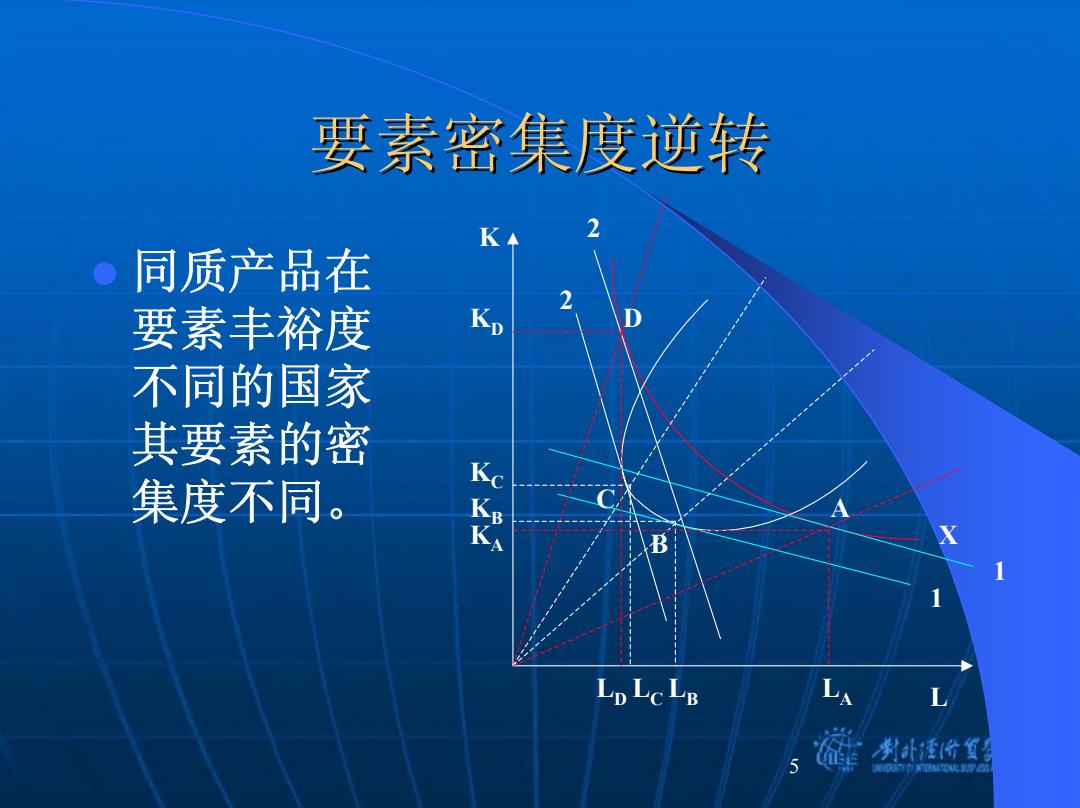
要素密集度逆转 K 同质产品在 要素丰裕度 Kp 不同的国家 其要素的密 集度不同。 LDLCLB LA 计至价質
5 要素密集度逆转 要素密集度逆转 K X 1 2 2 D C B A KD K C K B KA z 同质产品在 要素丰裕度 不同的国家 其要素的密 集度不同。 1 L D L C L B L A L