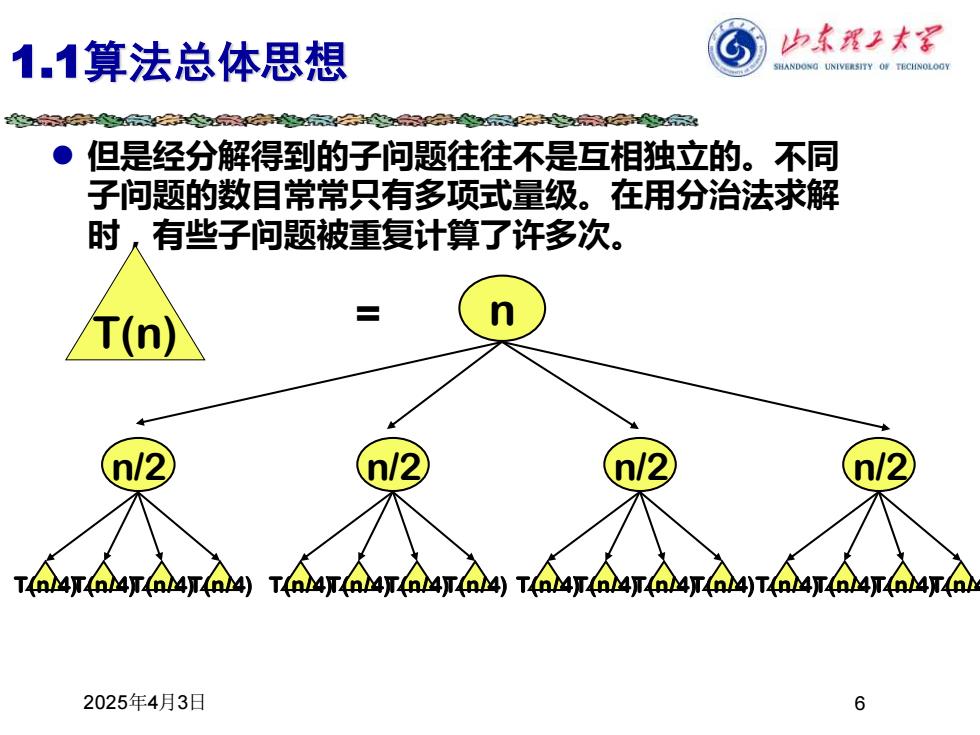
1.1算法总体思想 归东程子末军 SHANDONG UNIVERSITY OF TECHNOLOGY 5会器会的六会器会的品会 但是经分解得到的子问题往往不是互相独立的。不同 子问题的数目常常只有多项式量级。在用分治法求解 时有些子问题被重复计算了许多次。 T(n) n/2 n/2 n/2 TB 4X4R4T4R4T4R4)TR4T4R4T(B4T(R4)T(RM4X(B4T(R4X(R4)T(R4X(R4X4R4X4B 2025年4月3日 6
2025年4月3日 6 ⚫ 但是经分解得到的子问题往往不是互相独立的。不同 子问题的数目常常只有多项式量级。在用分治法求解 时,有些子问题被重复计算了许多次。 1.1算法总体思想 n T(n) = n/2 T(n/4)T(n/4)T(n/4)T(n/4) n/2 T(n/4)T(n/4)T(n/4)T(n/4) n/2 T(n/4)T(n/4)T(n/4)T(n/4) n/2 T(n/4)T(n/4)T(n/4)T(n/4)

1.1算法总体思想 归本理子太军 SHANDONG UNIVERSITY OF TECINOLOGY 会空空合会的尽会器会空器会合 如果能够保存已解决的子问题的答案,而在需要时再 找出已求得的答案,就可以避免大量重复计算,从而 得到多项式时间算法。 T(n) n/2 n/2 T(RM4)T(R4) TR4)T(R4)T(R4)T(R4)T(R4)T(R4)T44)T4RM4) T(n4) 2025年4月3日
2025年4月3日 7 ⚫ 如果能够保存已解决的子问题的答案,而在需要时再 找出已求得的答案,就可以避免大量重复计算,从而 得到多项式时间算法。 1.1算法总体思想 = n n/2 T(n/4) T(n/4) T(n/4) T(n/4) n/2 n/2 T(n/4)T(n/4) n/2 T(n/4) T(n/4) T(n/4) T(n/4) T(n/4) T(n)

归东程子末军 1.1总体思想 SHANDONG UNIVERSITY OF TECHNOLOGY 华器会空空合安会器空会的会路 动态规划算透与父迨清似石 某基本思想也是将待求解 问题分解成岩手不学同簸,但芬霹的学尚巅程挂不是 相互独立的。 Divide-.and-conquer技术的问题 ■子问题是相互独立的; 如果子闫题不是担县独立的,分治方法将重复计 算公共学简题,数率很低。 ●1 Dynamic Programming特点 ■把原始问题划分成一系列子问题; ■求解每个子问题区一次,并将基结果保存在个表中, 以后用到时直接荐取,不董复计算,节省计算时间; ■自底向上地计算。 2025年4月3日 d
2025年4月3日 8 1.1 总体思想 ⚫ 动态规划算法与分治法类似,其基本思想也是将待求解 问题分解成若干个子问题,但分解后的子问题往往不是 相互独立的。 ⚫ Divide-and-conquer技术的问题 ◼子问题是相互独立的; ◼如果子问题不是相互独立的,分治方法将重复计 算公共子问题,效率很低。 ⚫ Dynamic Programming特点 ◼ 把原始问题划分成一系列子问题; ◼ 求解每个子问题仅一次,并将其结果保存在一个表中, 以后用到时直接存取,不重复计算,节省计算时间; ◼ 自底向上地计算

归本理子太军 1.2适用范围 SHANDONG UNIVERSITY OF TECINOLOGY 会是33☆ ●适用范围 ■一类最优化问题:可分为多个相关子问题, 子问题的解被重复使用。 ● 最优化问题 ■给定一组约束条件和一个代价函数,在解空 间中搜索具有最小或最大代价的最优解; ■很多最优化问题可分为多个子问题,子问题 相互关联,子问题的解被重复使用。 2025年4月3日
2025年4月3日 9 1.2 适用范围 ⚫适用范围 ◼一类最优化问题:可分为多个相关子问题, 子问题的解被重复使用。 ⚫最优化问题 ◼给定一组约束条件和一个代价函数,在解空 间中搜索具有最小或最大代价的最优解; ◼很多最优化问题可分为多个子问题,子问题 相互关联,子问题的解被重复使用

归东理子太军程 1.3基本要素 SHANDONG UNIVERSITY OF TECHNOLOGY 华器会空空合安会空会的会 ●使用动态规划算法的条件: ■最优子结构(optimal sub-structure) ◆当一个问题的最优解包含了子问题的最优解时,称 这个问题具有最优子结构; ◆最优子结构使得能自底而上地完成求解过程; ◆通常可用“剪贴”(cut and paste))技术判定最优子结 构。 ■重叠子问题(overlapping sub-problems) ◆在问题的求解过程中,很多子问题的解将被多次使 用。 2025年4月3日 10
2025年4月3日 10 1.3 基本要素 ⚫使用动态规划算法的条件: ◼最优子结构(optimal sub-structure) ◆当一个问题的最优解包含了子问题的最优解时,称 这个问题具有最优子结构; ◆最优子结构使得能自底而上地完成求解过程; ◆通常可用“剪贴”(cut and paste)技术判定最优子结 构。 ◼重叠子问题(overlapping sub-problems) ◆在问题的求解过程中,很多子问题的解将被多次使 用