
归本程上太军 2.3贪心算法 SHANDONG UNIVERSITY OF TECINOLOGY 1.将所有活动按结束时间排序,得到活动集合 E={e1,e2.en}; 2.先将e1选入结果集合A中,即A={e1}; 3.依次扫描每一个活动e: 如果e的开始时间晚于最后一个选入A的活 动e的结束时间,则将e选入A中,否则放 弃e; 2025年4月3日 21
2025年4月3日 21 2.3贪心算法 1. 将所有活动按结束时间排序,得到活动集合 E={e1 ,e2.en }; 2. 先将e1选入结果集合A中,即A={e1 }; 3. 依次扫描每一个活动ei: 如果ei的开始时间晚于最后一个选入A的活 动ej的结束时间,则将ei选入A中,否则放 弃ei;

山东程子太军 SHANDONG UNIVERSITY OF TECHNOLOOY 2.3贪心算法 会是3会公☆ template<class Type> void GreedySelector(int n,Type s[,Type f[],bool A[]) A[1]=true; 各活动的起始时间和结 intj=1; 束时间存储于数组s和f 中且按结束时间的非减 for (int i=2;i<=n;i++){ 序排列 if (s[i]>=fj]){A[i]=true;j=i; else A[i]-false; 如果结束时间己排序:T(m)=O( 如果结束时间未排序:Tm)=Om)+O(nlogn)=O(nlogn 2025年4月3日 22
2025年4月3日 22 2.3贪心算法 template<class Type> void GreedySelector(int n, Type s[], Type f[], bool A[]) { A[1]=true; int j=1; for (int i=2;i<=n;i++) { if (s[i]>=f[j]) { A[i]=true; j=i; } else A[i]=false; } } 各活动的起始时间和结 束时间存储于数组s和f 中且按结束时间的非减 序排列 如果结束时间已排序: T(n)=O(n) 如果结束时间未排序: T(n)=O(n)+O(nlogn)=O(nlogn)
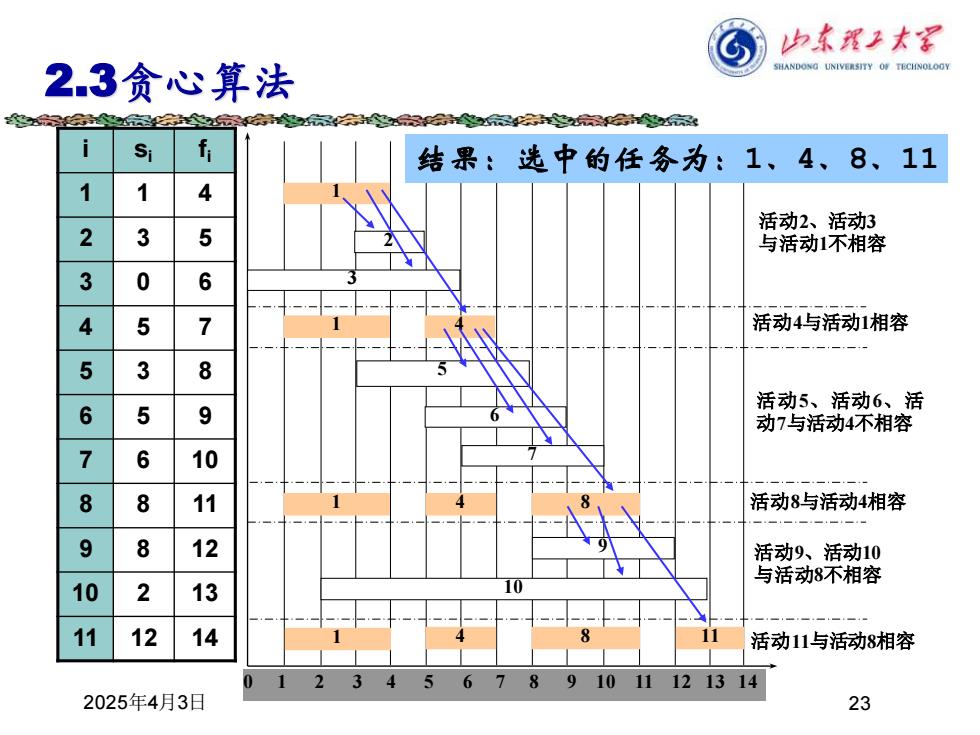
归东程子末军 2.3贪心算法 SHANDONG UNIVERSITY OF TECINOLOGY f 结果:选中的任务为:1、4、8、11 1 4 活动2、活动3 2 3 5 与活动1不相容 3 0 6 4 5 活动4与活动1相容 5 3 8 6 5 9 活动5、活动6、活 动7与活动4不相容 7 6 10 8 8 11 活动8与活动4相容 9 8 12 活动9、活动10 与活动8不相容 10 2 13 11 12 14 活动11与活动8相容 22 3 5 6 9 10 11 1213 14 2025年4月3日 23
2025年4月3日 23 2.3贪心算法 i si fi 1 1 4 2 3 5 3 0 6 4 5 7 5 3 8 6 5 9 7 6 10 8 8 11 9 8 12 10 2 13 11 12 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 3 1 2 1 4 6 7 8 9 10 1 4 8 11 4 活动2、活动3 与活动1不相容 活动4与活动1相容 活动5、活动6、活 动7与活动4不相容 活动8与活动4相容 活动9、活动10 与活动8不相容 活动11与活动8相容 5 结果:选中的任务为:1、4、8、11

归本程子末军 2.4算法正确性证明 HANDONG UNIVERSITY OF TECINOLOGY 需要证明: ■活动安排问题有一个最优解以贪心选择开始; ■活动安排问题具有最优子结构; ■算法每一步按照贪心选择计算,最终可得到原 问题的一个最优解。 2025年4月3日 24
2025年4月3日 24 2.4 算法正确性证明 ⚫需要证明: ◼活动安排问题有一个最优解以贪心选择开始; ◼活动安排问题具有最优子结构; ◼算法每一步按照贪心选择计算,最终可得到原 问题的一个最优解

归东理子太军 2.4算法正确性证明 SHANDONG UNIVERSITY OF TECINOLOGY 华器会空空合安会空会的会 定理1设E=l,2,n是n个话动集合,5.f/是活动 的起始终上时同,具f3≤.可n,E的话动安排 问题的某个最优解包括活动1. 证设A是一个最优解,按结束时间排序A中活动, 设其第一个活动为k,第二个活动尚j: 品果=1,定理成立. 品果kl,令B=A-U 由于A中活动相容,∫≤S,B中活动相容, 因为BA,所从B是一个最优解,具包格活动1. 灾理说明:活动终排问题有一个最优 解以个心选并开怡 2025年4月3日 25
2025年4月3日 25 定理1 设E={1,2,.,n}是n个活动集合,[si,f i ]是活动 的起始终止时间,且f 1 f 2 .f n,E的活动安排 问题的某个最优解包括活动1. 证 设A是一个最优解,按结束时间排序A中活动, 设其第一个活动为k,第二个活动为j. 如果k=1,定理成立. 如果k1,令B=A-{k}∪{1}, 由于A中活动相容,f 1 f k sj , B中活动相容. 因为B=A,所以B是一个最优解,且包括活动1. 2.4 算法正确性证明 定理1说明:活动安排问题有一个最优 解以贪心选择开始