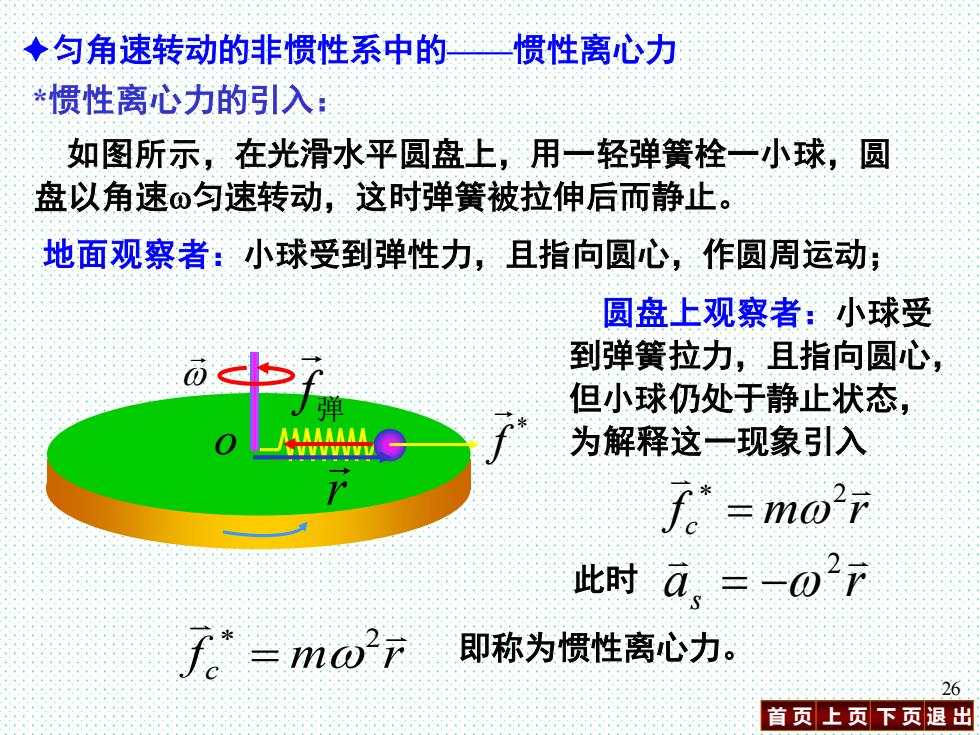
◆匀角速转动的非惯性系中的一惯性离心力 *惯性离心力的引入: 如图所示,在光滑水平圆盘上,用一轻弹簧栓一小球,圆 盘以角速ω匀速转动,这时弹簧被拉伸后而静止。 地面观察者:小球受到弹性力,且指向圆心,作圆周运动; 圆盘上观察者:小球受 到弹簧拉力,且指向圆心, 但小球仍处于静止状态, 为解释这一现象引入 f。=m02开 此时a.=-027 L"=mo'r 即称为惯性离心力。 26 首页上页下页退出
首 页 上 页 下 页 退 出 26 匀角速转动的非惯性系中的——惯性离心力 *惯性离心力的引入: 如图所示,在光滑水平圆盘上,用一轻弹簧栓一小球,圆 盘以角速匀速转动,这时弹簧被拉伸后而静止。 地面观察者:小球受到弹性力,且指向圆心,作圆周运动; 圆盘上观察者:小球受 到弹簧拉力,且指向圆心, 但小球仍处于静止状态, 为解释这一现象引入 f m r c 2 = a r s 2 此时 = − f m r 即称为惯性离心力。 c 2 = f 弹 * f r o

*地球自转对重力的影响 以地球为参照系,考虑地球的自转,于是地面上任何 一个物体都是在三个力: @C 支持力N。、引力F引、惯性离性力f 作用下处于平衡态, 而地面上的观察者通常总是把地面上 的物体作二力平衡来处理,即认为物 体在重力W和支持力N作用下达到平 衡态, 因此重力W实际上应是F和f的合 力,即: W2=F2引+f”-2F·f"cos 由是得 *-r写-2m的 27 首页上页下页退出
首 页 上 页 下 页 退 出 27 *地球自转对重力的影响 支持力N、引力F引、惯性离性力ƒ * c 作用下处于平衡态, 而地面上的观察者通常总是把地面上 的物体作二力平衡来处理,即认为物 体在重力W和支持力N作用下达到平 衡态, 因此重力W实际上应是F引和ƒ * c的合 力,即: 2 cos 2 2 *2 * c c W = F 引 + f − F引 f 2 1 * 2 * [1 ( ) 2 cos] 引 引 引 F f F f W F c c 由是得 = + − N F引 ƒ * c W 以地球为参照系,考虑地球的自转,于是地面上任何 一个物体都是在三个力:
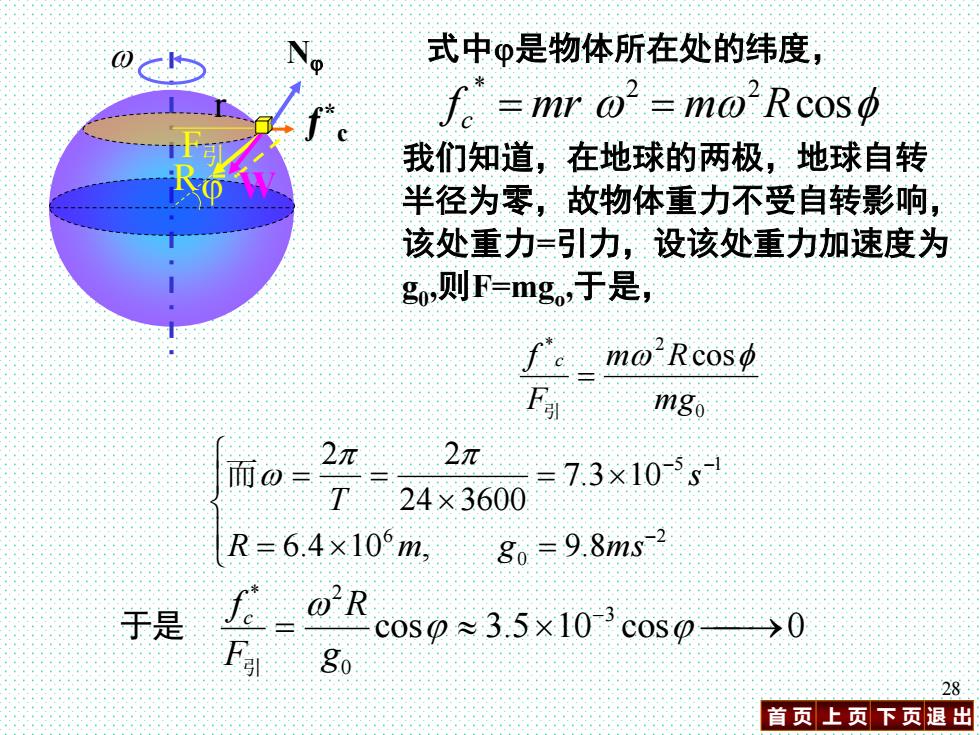
@c No 式中φ是物体所在处的纬度, f。=mro2=mo2Rcos中 我们知道,在地球的两极,地球自转 半径为零,故物体重力不受自转影响, 该处重力=引力,设该处重力加速度为 g,则F=mg,于是, f'c_mo'Rcos F mgo 而w 2π =7.3×105s 24×3600 R=6.4×10m, 80=9.8ms-2 于是 Rcos3.5x10cs F 0→0 80 28 首页上页下页退出
首 页 上 页 下 页 退 出 28 我们知道,在地球的两极,地球自转 半径为零,故物体重力不受自转影响, 该处重力=引力,设该处重力加速度为 g0 ,则F=mgo ,于是, 0 * 2 cos mg m R F f c = 引 = = = = = − − − 2 0 6 5 1 6.4 10 , 9.8 7.3 10 24 3600 2 2 R m g m s s T 而 cos 3.5 10 cos 0 3 0 * 2 = − ⎯→ g R F f c 引 于是 式中是物体所在处的纬度, * 2 f c = mr F引 ƒ * c W r R N cos 2 = m R

即 £=35×10'c0s0)0是-个无穷小量, #-Fnm明 略去高阶无穷小量 华=F1-2cs列 F 利用二项式定理 0+x对=1+m42-x2+n-a-2x+ 2 3 再次略去高阶无穷小,得 W=F0- cos) F 3.5x10cos-Fa(1-3.5x10cos) 29 首页上页下页退出
首 页 上 页 下 页 退 出 29 2 * 1 (1 2 cos) 引 引 F f W F c = − 2 1 * 2 * [1 ( ) 2 cos] 引 引 引 F f F f W F c c = + − 2 * ( ) F引 f c 略去高阶无穷小量 得 即 3.5 10 cos 0 是一个无穷小量, 3 * = − ⎯→ F引 f c 利用二项式定理 ( ) ( ) ( )( ) + − − + − + = + + 2 3 3! 1 2 2! 1 1 1 x n n n x n n x nx n 再次略去高阶无穷小,得 (1 3.5 10 cos ) 3 2 − W = F引 − (1 cos ) * 引 引 F f W F c = − 3.5 10 cos 3 * − F引 f c

:.W=F(1-3.5×10-3cos2) 可见地面上物体的重力大小随纬度而变化,其方向也不严 格指向地心,—故常说重力方向为铅垂方向,但由结果看 出,重力随纬度变化并不明显,通常可以忽略。 30 首页上页下页退出
首 页 上 页 下 页 退 出 30 可见地面上物体的重力大小随纬度而变化,其方向也不严 格指向地心,——故常说重力方向为铅垂方向,但由结果看 出,重力随纬度变化并不明显,通常可以忽略。 (1 3.5 10 cos ) 3 2 − W = F引 −