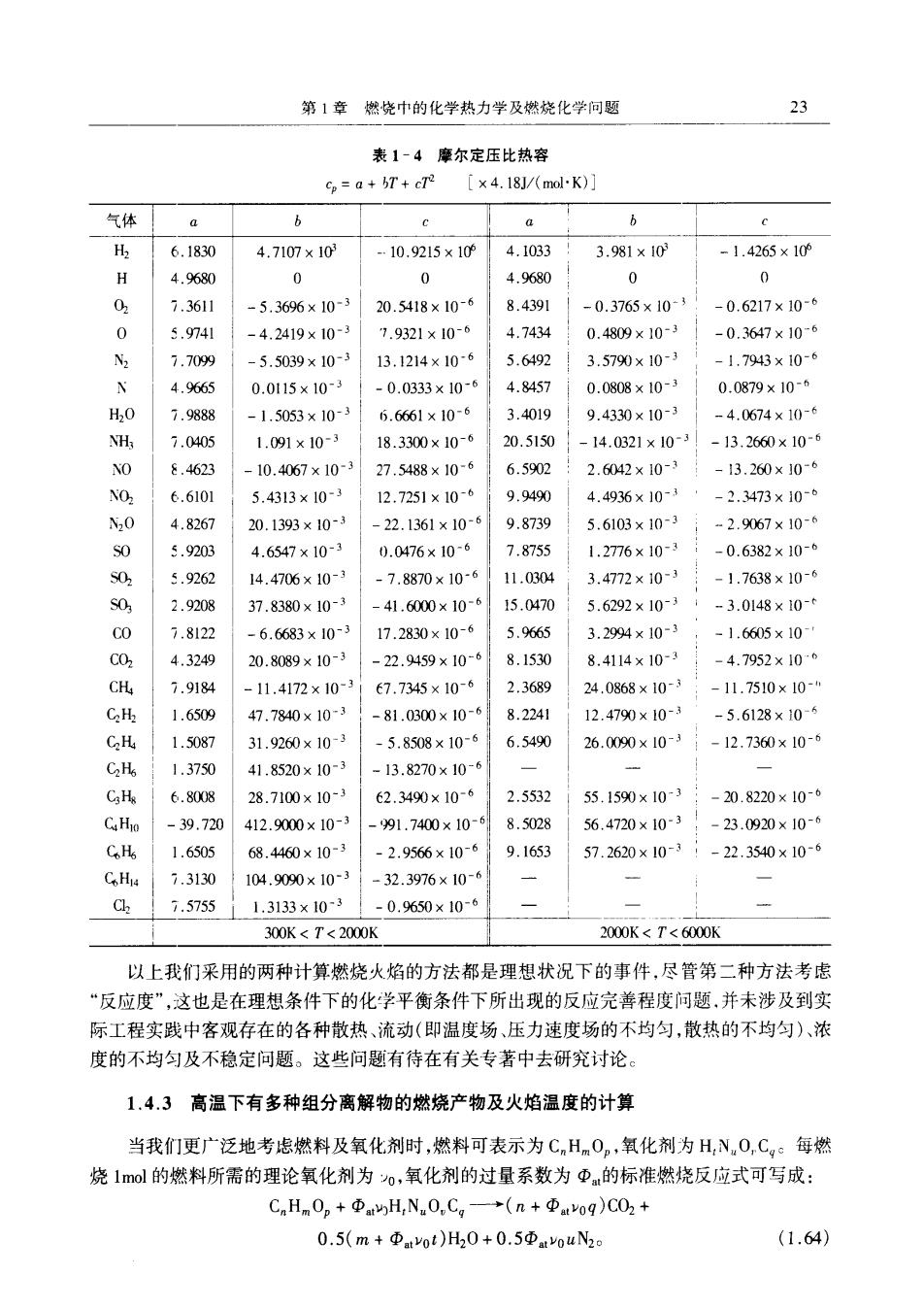
第1章燃烧中的化学热力学及燃烧化学问盟 23 表1-4摩尔定压比热容 =a+T+cT2 [×4.l8J/mol-K)] 气体 a b a b 6.1830 4.7107×103 10.9215×10 4.1033 3.981×10 -1.4266×10 H 4.9680 0 0 4.9680 0 0 02 7.3611 -5.3696×10 20.5418×10- 8.4391 -0.3765×10- -0.6217×10 0 5.974I -42419×10- 7.9321×10-6 4.7434 0.4809×10-3 -0.3647×10-6 2 7.709 5.5039×10- 13.1214×10-6 5.6492 3.5790×10-3 1.7943×10-6 4.9665 0.0115×10- 0.0333×10-6 4.845 0.0808×10- 0.0879×10-0 H,0 7.9888 -1.5053×10 5.6661×10-6 3.401g 9.4330×10-3 -4.0674×10-6 NH 7.040 1.091×10- 18.3300×10-4 20.5150 -14.0321×10 -13.2660×10- NO 8.4623 -10.4067×10-3 27.5488×10-6 6.5902 2.6042×10-3 -13.260×106 NO. 6.610 5.4313×10- 12.7251×10-1 9.949 4.4936×10- -2.3473×10 ,0 4.8267 20.1393×10- 22.1361×10-6 0.8729 5.6103×10-3 -2.9067×10-9 5.920 4.6547×10- 0.0476×10- 7.8755 1.2776×103 -0.6382×10- 5.9262 14.4706×10- .7.8870×10-6 】1.0304 3.4772×10-3 -1.7638×10-6 S0, 2.9208 37.8380×10- -41.6000×10 15.0470 5.6292×103 -3.0148×0- 7.8122 -6.6683×10- 17.2830×10-4 5.9665 3.2994×10-3 -1.6605x10 4.3249 20.8089×10- -22.9459×10-6 8.1530 8.414×10-3 -4.7952×106 7.9184 -11.4172×10 E7.7345×10-4 2.3689 24.0868×10- -11.7510×10- C 1.6509 47.7840×10 81.0300×10-9 8.2241 12.4790×103 -5.6128x10-6 C.H 1.5087 31.9260×10- 5.8508×10-9 6.5490 26.0090×10 12.7360×10-6 1.3750 41.8520×10-3 -13.8270×10 6.8008 28.7100×10- 62.3490×10-4 2.5532 55.1590×10 -20.8220×10 .39.720 412.9000×10- 91.7400×10- 8.5028 56.4720×10-3 -23.0920×10-6 C.H 1.6505 68.4460×10- 2.9566×10- 9.1653 57.2620×10- -22.3540×10-6 CHu 7.3130 104.9090×10-3 32.3976×10- 7.57551.3133×10 -0.9650×10- 300K<T<2000K 2000K<T<6000K 以上我们采用的两种计算燃烧火焰的方法都是理想状况下的事件,尽管第二种方法考店 “反应度”,这也是在理想条件下的化学平衡条件下所出现的反应完善程度问题,并未涉及到实 际工程实践中客观存在的各种散热、流动(即温度场、压力速度场的不均匀,散热的不均匀)、浓 度的不均匀及不稳定问题。这些问题有待在有关专著中去研究讨论。 1.4.3高温下有多种组分离解物的燃烧产物及火焰温度的计算 当我们更广泛地考虑燃料及氧化剂时,燃料可表示为CnH0,氧化剂为H,N0,C。每燃 烧10l的燃料所需的理论氧化剂为o,氧化剂的过量系数为Φ的标准燃烧反应式可写成: CHn0p+ΦmyH,N0,Cg一→(n+Φmoq)C02 0.5(m+Φtyot)H20+0.5ΦtouN2 (1.64
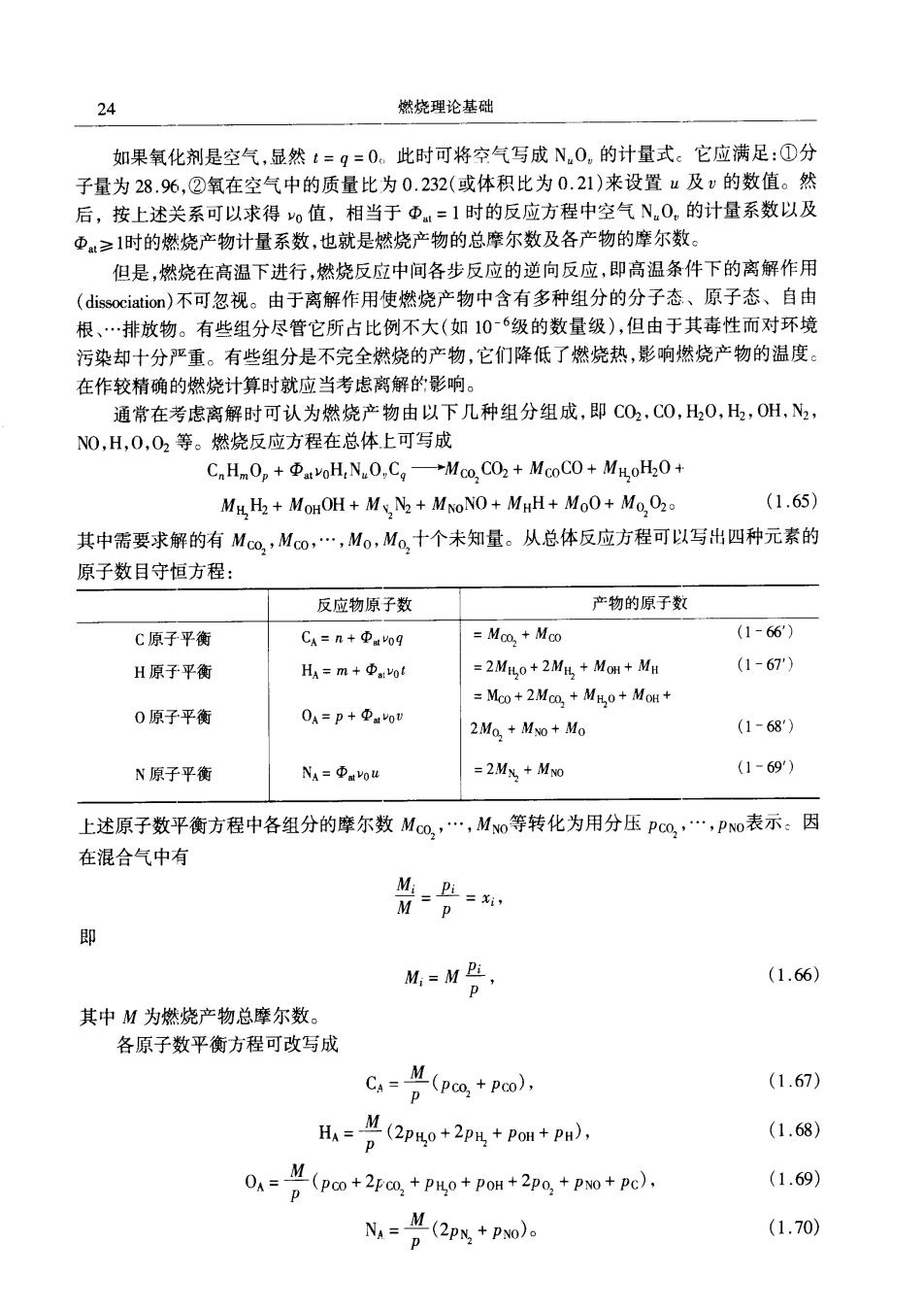
24 燃烧理论基础 如果氧化剂是空气,显然t=g=0。此时可将空气写成N0,的计量式。它应满足:①分 子量为28.96,②氧在空气中的质量比为0.232(或体积比为0.21)来设置4及v的数值。然 后,按上述关系可以求得o值,相当于中=1时的反应方程中空气N0,的计量系数以及 中≥1时的燃烧产物计量系数,也就是然烧产物的总摩尔数及各产物的摩尔数。 但是,燃烧在高温下进行,燃烧反应中间各步反应的逆向反应,即高温条件下的离解作用 (dissociation)不可忽视。由于离解作用使燃烧产物中含有多种组分的分子态、原子态、自由 根、排放物。有些组分尽管它所占比例不大(如10-6级的数量级),但由于其毒性而对环境 污染却十分严重。有些组分是不完全燃烧的产物,它们降低了燃烧热,影响燃烧产物的温度。 在作较精确的燃烧计算时就应当考虑离解的影响。 通常在考虑离解时可认为燃烧产物由以下几种组分组成,即CO2,CO,H20,H2,OH,N2, N0,H,0,02等。燃烧反应方程在总体上可写成 C.HmO+oH.N.O.C-Mco,CO2+McoCO+MHoH2O+ MH.H2+MoHOH+Ms.N2+MNoNO+MHH+MoO+Mo,02 (1.65) 其中需要求解的有Mo,Mco,·,Mo,Mo,十个未知量。从总体反应方程可以写出四种元素的 原子数目守恒方程 反应物原子数 产物的原子数 C原子平衡 C=n+中eg Moo.Moo (1-66) H原子平衡 HA=m =2ML,0+2MH+Mo刚+MH (1-67) Moo+2Mo,+Mio+Mo+ 0原子平衡 2Mo,+Mwo+Mo (1-68') N原子平衡 NA=币aou =2Mx MNo (1-69) 上述原子数平衡方程中各组分的摩尔数Mm,,Mo等转化为用分压Pm,Po表示。因 在混合气中有 M.-MP (1.66) 其中M为燃烧产物总摩尔数 各原子数平衡方程可改写成 C=(poo,+poo) (1.67) (m2m+pon+p). (1.68) 0=兰@+24a*p0*pom+2p%*pm+pe. (1.69) (2px+px). (1.70)

第1章燃经中的化学热力学及燃烧化学问题 25 尚需六个方程才能对M,等十个未知数求解。以下六个中间反应方程是烃燃料燃烧中的重 要中间基元反应: C02一C0+0.50 (1.71') H,0=H2+0.502 (1.72) H20-=0H+0.5H2, (1.73 H一2H, (1.74') 02=20, (1.75) 0.5N2+0.502=N0。 (1.76) 在燃烧过程中可认为上述中间反应过程处于平衡状态,它们的平衡常数可写成: (1.71) Pco K0sPgp吸5 (1.72) PHo K3= Poups (1.73) K得 (1.74) (1.75) Kwe-popo (1.76) 此外,各分压之和应为全压P,有 Pco,Pco+PHoPH PoH Po,+Px +PH+Px=po (1.77) 于是,按式(1.67)式(1.77)等11个方程式可以求得M,Po,Po等11个待求参数值。再按式 (1.66)可求得燃烧产物中各组分摩尔数M:及摩尔比x0 由于各组分分压P,(或摩尔比x)与平衡常数K不呈线性关系,平衡常数K:又是温度T: 的函数值(需要预置),用消去法求解比较困难。为此,一般常常用计算迭代法求解 在初步求得燃烧产物组分的摩尔数M:之后即可求出燃烧温度,按热力学第一定律,有 -aie=∑7 McpdT。 (1.78) 这里求得的T值与求解各组分时预置的T值不等时,可用所求得的T,重新迭代作燃烧 产物组分计算,直到前后误差小于许可值为止。 1.5燃烧的反应速度 在本章前面几节,讨论了燃料燃烧时化学能与热能间能量转换的数量关系及理想条件下 燃烧反应的完善程度。下面将对燃烧的反应速度问题进行讨论

26 燃烧理论基础 1.5.1净反应速度 值得一提的是:在前面几节中我们所讨论的化学平衡计算只能适用于基元反应。而实际 然烧反应都是由许多个相继发生的基元反应所构成的复杂反应。一些基元反应中的产物,立 即成为另外一些基元反应的反应物而被消耗掉。在确定某一反应物或产物的反应速度时必须 要了解在构成此复杂的各基元反应中,有哪些基元反应与讨论的化合物有关,再从这些基元反 应中对该化合物的消耗速度及生成速度计算出它的净反应速度。 从化学反应的质量作用定律已知,基元反应式(1.12)的反应速度为式(:.16)、式(1.17)所 示,即 正向反应速度为: i=n=kr[A][B]b 逆向反应速度为: 7=rb=k[C]c[D]4。 因反应进行过程中同时存在两个方向的反应,可认为此一特定反应的正向的净反应速度为 r=-=[A]4[B]6-kp[C][D]4 (1.79) 对于那些由若干个基元反应所构我的复杂反应而言,对于某一种反应物或反应产物的净 反应速度与其反应机构有关,反应系统中某一化合物的净反应速度是该化合物在各个基元反 应中的消耗速度与生成速度的代数和,在链反应一节中将举例说明。 1.5.2反应级数与反应分子数 由式(1.16)、式(1.17)所表达的质量作用定理关系可知,反应速度与反应物浓度存在着 定的量级关系。浓度因子[A]及[B]的指数和(a+b)及[C]及[D]的指数和(c+d),称之为反 应级数,一般由试验决定。但当反应为基元反应时,反应式中各化合物的计量系数代表了该化 合物在反应时相互作用的分子数目关系。这时,反应级数与反应分子数的数值相等。如基元 反应为 aA+bB→cC+dD, 则反应分子数为a+b,反应级数也是a+b。 常见的许多反应大多是复杂反应,尤其是燃烧反应更为复杂而迅速,它的反应级数均由试验 决定。一般烃类的碳氢化合物燃料的燃烧反应级数为1.7~2.2。这种复杂反应的中间过程十分复 杂,至今还没有完全弄明白其全部反应机构。因而,也就无法讨论它们的反应分子数问题。 决定反应级数的另一种方法是通过试验测定反应物浓度随时间变化的关系,它的原理如下: 当化学反应式为式(1.12)时,其反应速度为 -A=k[A][B], dt 由于反应时各反应物间存在一定的化学计量比关系,上式又可写成 -=6, 在等温条件下反应的比反应速度kn为常数,上式又可改写成 -k
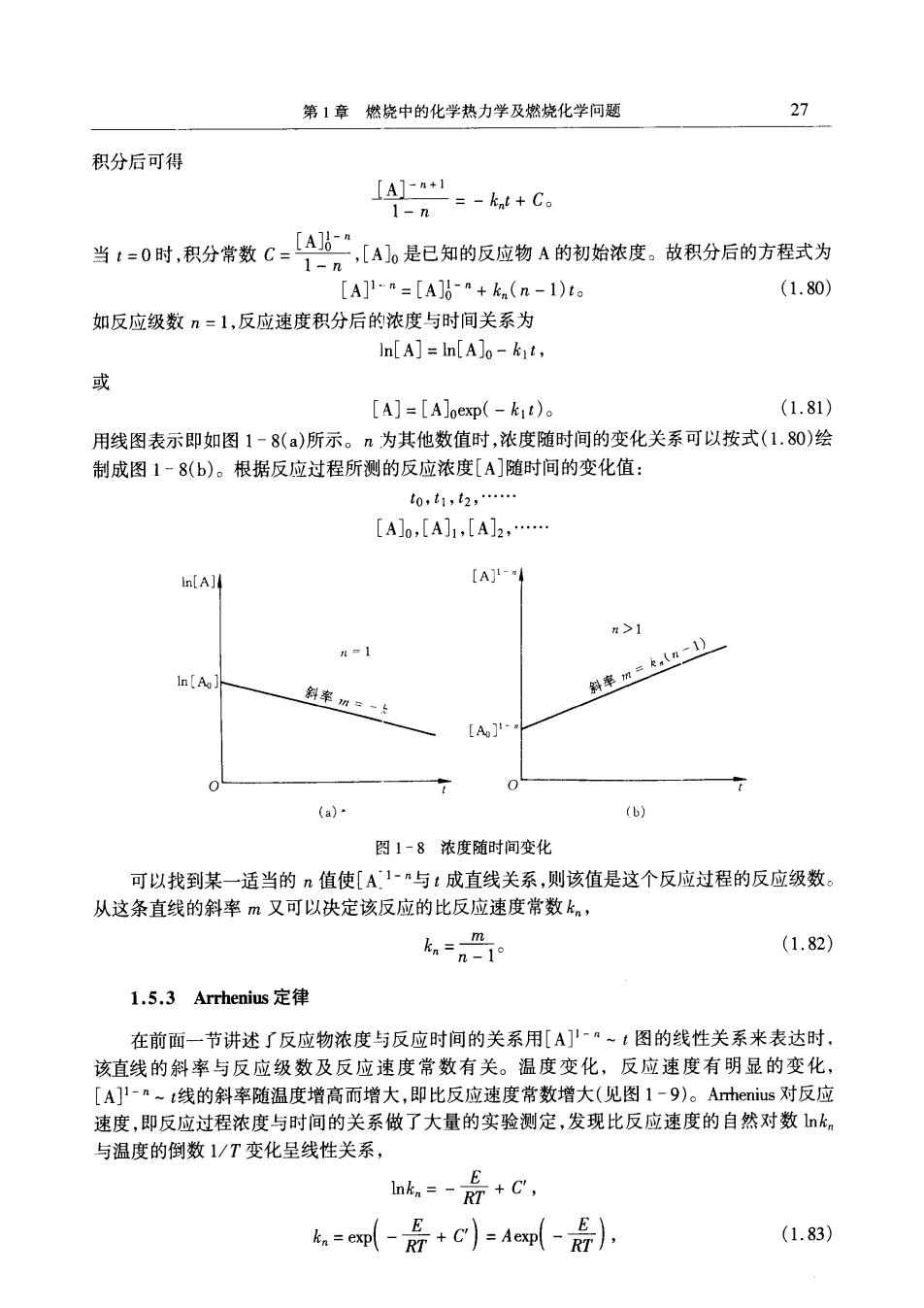
第1章燃烧中的化学热力学及燃烧化学问题 27 积分后可得 [A1=-k+C 1-n 当1=0时,积分常数C:二【A。是已知的反应物A的初始浓皮。放积分后的方程式为 [A]1-n=[A]0-a+kn(n-1)ta (1.80) 如反应级数n=1,反应速度积分后的浓度与时间关系为 In[A]=In[A]o-kit, 或 [AJ=[A]oexp(-k1t)。 (1.81) 用线图表示即如图1-8(a)所示。n为其他数值时,浓度随时间的变化关系可以按式(1.80)绘 制成图1-8(b)。根据反应过程所测的反应浓度[A]随时间的变化值: t0,t1,2, [A]0,[A]1,[A]2, in[A]4 [A]- >1 1 [Ag 斜率m=k,《) 斜率一 [Ao 人 (a) (b) 图1-8浓度随时间变化 可以找到某一适当的n值使[A1-n与t成直线关系,则该值是这个反应过程的反应级数。 从这条直线的斜率m又可以决定该反应的比反应速度常数k, ka=n-1° (1.82) 1.5.3 Arrhenius定律 在前面一节讲述了反应物浓度与反应时间的关系用[A]'-·~1图的线性关系来表达时 该直线的斜率与反应级数及反应速度常数有关。温度变化,反应速度有明显的变化, [A]1-n~t线的斜率随温度增高而增大,即比反应速度常数增大(见图1-9)。Arhenius对反应 速度,即反应过程浓度与时间的关系做了大量的实验测定,发现比反应速度的自然对数k。 与温度的倒数1/T变化呈线性关系, hk,=-后+C, k=em-是+c)=Aem-后), (1.83)