
8 燃烧理论基础 正向反应速度 7=r=kdLA]e[B]6, (1.16) 逆向反应速度 n=kb[C][D]4 (1.17) 当反应系统未到达平衡时,≠。当系统达到平衡时,即反应系统中各种反应物及产物 的浓度均已稳定不变,则正反向反应速度相等, 「(=Tb=r, (1.18) [A:[B]=[C][D]4 (1.19) 点邵=人 (1.20) 式中:k、k为正向(比)反应速度常数及逆向(比)反应速度常数;K。为按浓度定义的反应平衡 常数 当反应系统中各种物质均服从理想气体定律时,浓度[]可写成: A]==治 B==得 (1.21) d-晋=路 罗器 以上诸式中:n,,nn及PA,Pn分别为物质A,B,C,D的摩尔数及分压;V,T为反应系统 的体积及温度;R为通用气体常数。平衡常数K,又可写成 k-2-(爱 (1.22) 其中△n=(c-d)-(a+b)反应产物与反应物分子数的变化。令 K--叠d (1.23) 为以分压或物质的体积百分比定义的平衡常数。其中xA,xB,xC,xD分别为A,B,C,D在反应 系统中的体积(或摩尔)百分比,P为反应系统的全压,平衡常数K。与K,的关系为 Ke=(RT)-AnK. (1.24) 从上述分析可知,当系统中的化学反应进行达到平衡时,系统中反应物A,B及产物C,D 间浓度的关系应满足式(1.20),或它们的分压或体积(或摩尔)百分比应满足式(1,23)。只要 平衡常数K或K,为有限值,则反应达到稳定平衡后系统内仍有少量反应物A,B存在(即有 [A],[B],PAPB及xAx存在),反应物A,B并不能全部地变成C.D。显然.K或K,的值越 大,正向反应进行得越完全,系统平衡时残留的反应物愈少,这是因为正向反应速度(以比反应 速度常数:表示)远比逆向反应速度(用表示)大得多的缘故。 这种有限度的反应可用反应度入来表达,入代表了反应系统到达平衡时反应物能有效地
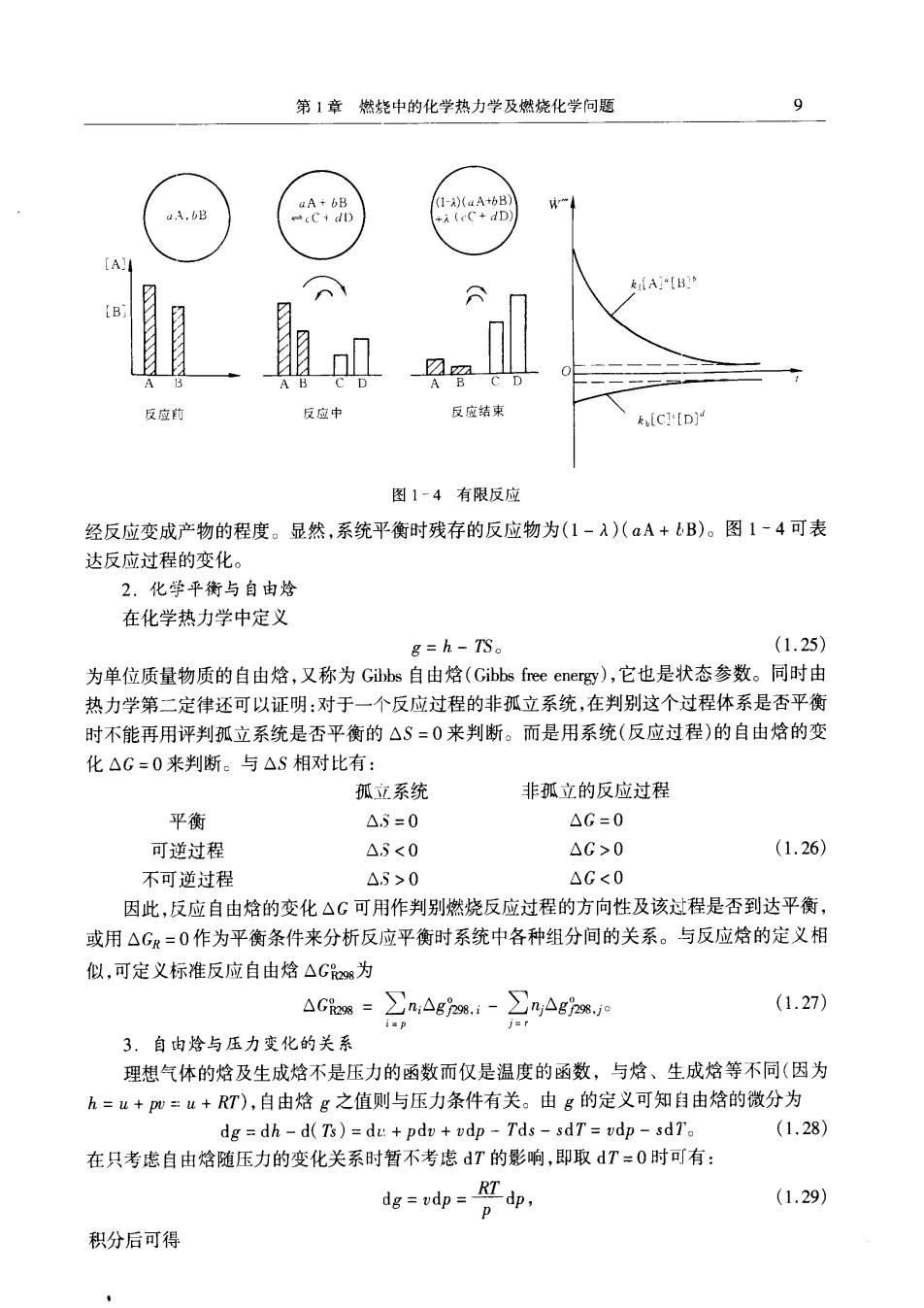
第1章燃烧中的化学热力学及燃烧化学问题 A.tB 反应的 反应中 反应结束 [C[D] 图1-4有限反应 经反应变成产物的程度。显然,系统平衡时残存的反应物为(1-入)(aA+bB)。图1~4可表 达反应过程的变化。 2.化学平衡与自由烩 在化学热力学中定义 g=h-S。 (1.25) 为单位质量物质的自由焓,又称为Gibs自由焓(Gibbs free energ),它也是状态参数。同时由 热力学第二定律还可以证明:对于一个反应过程的非孤立系统,在判别这个过程体系是否平衡 时不能再用评判孤立系统是否平衡的△S=0来判断。而是用系统(反应过程)的自由焓的变 化△G=0来判断。与△S相对比有: 孤立系统 非孤立的反应过程 平衡 △5=0 △G=0 可逆过程 △5<0 4G>0 (1.26) 不可逆过程 △5>0 △G<0 因此,反应自由焓的变化△G可用作判别燃烧反应过程的方向性及该过程是否到达平衡, 或用△GR=0作为平衡条件来分析反应平衡时系统中各种组分间的关系。与反应焓的定义相 似,可定义标准反应自由焓△G为 aGiw=2n△gn4-∑nag7 (1.27) 3.自由焓与压力变化的关系 理想气体的焓及生成焓不是压力的函数而仅是温度的函数,与焓、生成焓等不同(因为 k=u+Pm=u+RT),自由焓g之值则与压力条件有关。由g的定义可知自由焓的微分为 dg=dh-d(Ts)=du+pdv+vdp-Tds-sdT=vdp-sdT. (1.28) 在只考虑自由焓随压力的变化关系时暂不考虑T的影响,即取dT=0时可有: dedpdp. (1.29) 积分后可得

10 燃烧理论基础 af-ei=m业=mn片 (1.30) 即在恒温条件下由于压力变化引起的自由焓的增量与压力变化比的自然对数值成正比 4.自由焓与温度变化的关系 在分析自由焓与温度变化的关系时可暂时不顾及压力的影响,即认为按dp=0的条件作 分析。 由于自由焙为一状态参数,可写作 g=g(p.T), 故有 dg=(器)dr+(那),n. (1.31) 与式(1.28)t较后,有 (器),=s及3,= (1.32) 对任一特定的温度条件下式(1.28)又可写作 dg=dh-Tds, 或 Ag=△h-T△s (),=-a, 合并上述两式可得 ()=84 (1.33) 这就是Gibbs-Helmholtz方程式,它表达了在定压条件下自由焙随温度的变化情况。但是,为 了数值运算比较方便,还可将两式改变形式为 最后得 ()) (1.34) 这样,在定压条件下某一特定温度时自由焓的变化可以用该过程熔的变化△h来表达,使计算 更为方便,是Gibbs-Helmholtz方程的另一种表达形式。 5.平衡常数K,与标准反应自由洛 本节将讨论化学反应平衡常数的确定方法,并且平衡常数仅由基元反应式及反应时的温 度所决定。平衡常数K。可用不同方法计算,在这里仅用生成烙来计算。与标准生成焓的定 义相同来定义化合物的标准生成自由培。 化合物的标准生成自由烙△g?是由化合物的构成元素在标准状态下经化合反应生成 1ml的该化合物时的自由焓的增量。同理,元素的生成自由焓为零

第1章燃烧中的化学热力学及燃烧化学问题 11 通过压力与自由焓变化间的关系可以求得平衡常数。 当化学反应为 aA+bB→cC+dD 时,其标准反应自由焓为 △Cw=clg7.+d△g。-a△g7,-b△gia (1.35) 而实际的反应自由焓为 △Gi=c△g+d△g-a△g-b△g, (1.36 其中式(1.35)所表达的各组分的生成自由焙△g.、△g%等都是在一个大气压下的数值.式 (1.36)所表达的各个生成自由焓△g、△g2、…都是相应地处于自己的分压状态(即p·Pm P4PB)下的实际值。式(1.36)与式(:.35)之差系压力变化引起的反应自由焓的变化 △G限-△G=c(△g-△g,)+d(△g7-△g,)-a(△g盼-△g阶,)-b△g-△g3) RT(clnpc+dlnpp-alnpa-blnpB) =m盛 当反应达到平衡时则必然有△C=0,则上式变成 -AGR=RTip (1.37) 又可写成 Ink, (1.37) 式中:△G所这个标准反应自由格是由反应方程式中各反应物、产物的标准生成自由焓 △g,…,△g,及计量系数a,b,c,d所决定的,不因反应条件而变的常数。因此,平衡常数K, 只是温度的函数 各种物质的生成自由焓可以从有关的化学热力学手册查得,表1-2表示了一些常见物质 的生成自由焓。 根据式(1.37)可以找到各种化学反应在指定温度T时的平衡常数K。,平衡常数K。、K。是 反应平衡时在反应系统中各产物与残存反应物的分压(或体积百分比)或浓度间所应满足的数 量关系。如式(1.20)及式(1.23)所示。 为了便于查阅计算,这里将一些基元反应的化学平衡常数列在表1-3中。值愈大.则正 向反应速度愈大,反应进行得愈彻底,相反,如某一反应的平衡常数K,值随温度增高而减少, 则该反应达到产物在高温时愈容易分解,逆向反应的速度增加。 6.反应度1 从化学反应平衡原理已知,任何一种化学反应都有一平衡的状态存在.反应物经反应变换 成产物的程度也是有限的。这种反应程度可用反应度入来表示。如图1-4所示,当反应系统 在特定的、T条件下达到平衡时,系统内的反应物对产物间的数量关系可表达为 反应开始时 反应平衡时 aA+bB-(I-a)(aA+bB)+(cC+dD), (1.38) 显然,平衡时系统内各种化合物的数量关系应满足式(1.23)

12 燃烧理论基础 (1.23) 其中,平衡时系统内各化合物的摩尔百分比为: a(1-λ) xA=(1-A)(a+b)+A(c+d)' =a-c+d c=0-a+6+Ae+ xD=(1-入)(a+b)+(c+d)° (1.39) 表1-2一些物质的生成自由焓△g(4.186k/m0l) 物质 △gs 物质 △g 0 -54.64 甲烷CH -12.14 0 39.06 乙院CH -7.86 册 2.n 丙烷CH -丁烷CHo 56 -12.72 -3. 0.31 异丁烷CHo -4.30 SO. -71.79 一戊烷CH2 -1.96 .88.52 异戊烷CH2 -3.50 7.89 新成烷CH2 -3.60 24.90 乙烯C 16.28 NO 20.72 乙快CH 50.00 NO 12.39 1一丁烯C,e 17.22 -3.97 顺-2-丁烯C,H 15.74 32.81 反一2-丁烯CH 15.05 -94.26 异丁烯C 13.88 48.58 13-丁二烯CH6 36.01 14.20 氯甲烷CHd -14.00 甲醇CHOH 3073 969 乙醇CH0H -41.n 16.77 乙酸CL02 -93.80 160.85 苯CH 31.00 81.47 三氯甲烷CHC -17.10 54.99 四氯化碳CCL -16.40 由于反应条件p、T为已知,化学平衡常数只是温度的函数,可由式(1.37)或查表求得。将式 (1.39)代人式(1.23)后可以求得相应的反应度A。随即平衡时各种反应物与产物的摩尔比x,…, xD可以求得;应用式(1.20)的关系也可以求得各物质的平衡浓度[A],[B],[C],[D]。 例:氢-氧在3000K0.1MPa条件下进行 H+702→0 (a) 反应,试求反应平衡时的反应度及各物质的摩尔比。 解:式(a)的逆反应为