
例三 若光源$上移,则屏上接收的条纹有何变化? 答:条纹下移
例三 S S O O 答:条纹下移 若光源s上移,则屏上接收的条纹有何变化?

例四 杨氏实验中,如果电光源由两个波长入,=550nm、 入,=500nm组成,两缝间距d=0.1cm,缝与屏的距离为 D=500cm,求(1)每一波长干涉条纹的宽度。(2)两个波长 的亮条纹第一次重合的位置(不包括零级条纹) 。 解:看不到干涉条纹的条件: 前一级极大=后一级极大 k×长波长=(k+1)短波长 550k=500(k+1) K=10
例四 杨氏实验中,如果电光源由两个波长 、 组成,两缝间距d=0.1cm,缝与屏的距离为 D=500cm,求(1)每一波长干涉条纹的宽度。(2)两个波长 的亮条纹第一次重合的位置(不包括零级条纹)。 1 = 550nm 2 = 500nm 解: 看不到干涉条纹的条件: 前一级极大=后一级极大 k长波长=(k+1)短波长 550k=500(k+1) K=10

三、薄膜干涉实验 n I one 2 two three 。比较振幅
三、 薄膜干涉实验
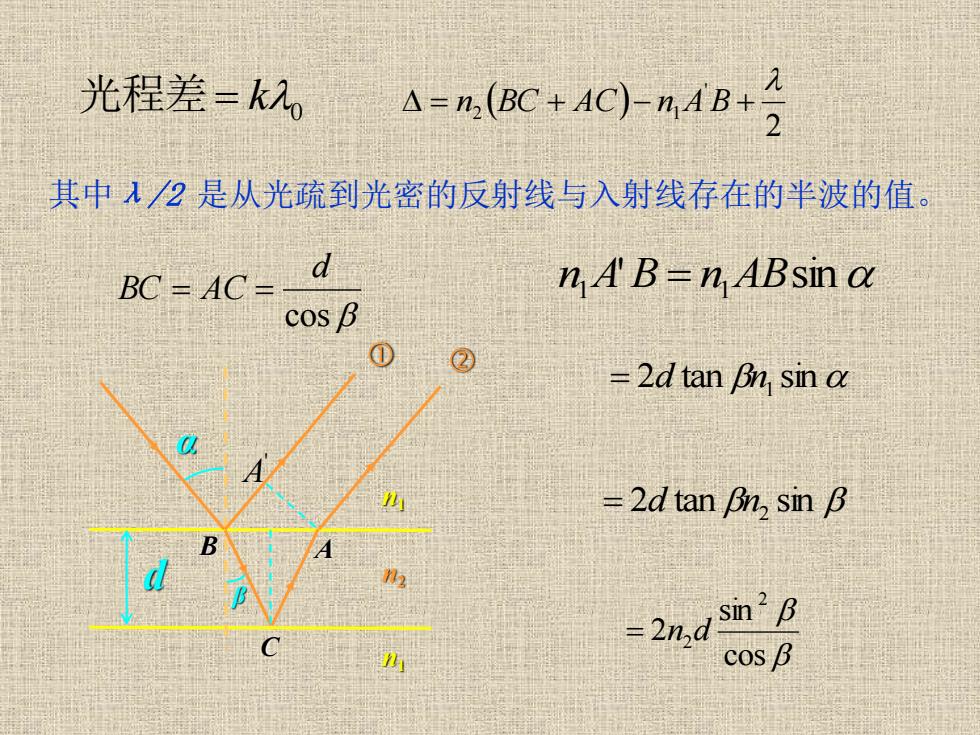
光程差=k, 4=%(+4C)-4B+ 其中入2是从光疏到光密的反射线与入射线存在的半波的值。 d BC=AC= n A B=n ABsin a cos B ① ② =2d tan Bn sin a -2 d tan Bn2sin阝 =2nd sin'B cos B
0 光程差= k ( ) 2 ' 2 1 = n BC + AC − n A B + cos d BC = AC = 其中λ/2 是从光疏到光密的反射线与入射线存在的半波的值。 n1 A'B = n1 ABsin = 2d tan n1 sin = 2d tan n2 sin cos sin 2 2 = n2 d α d β B C A n1 n2 n1 ' A
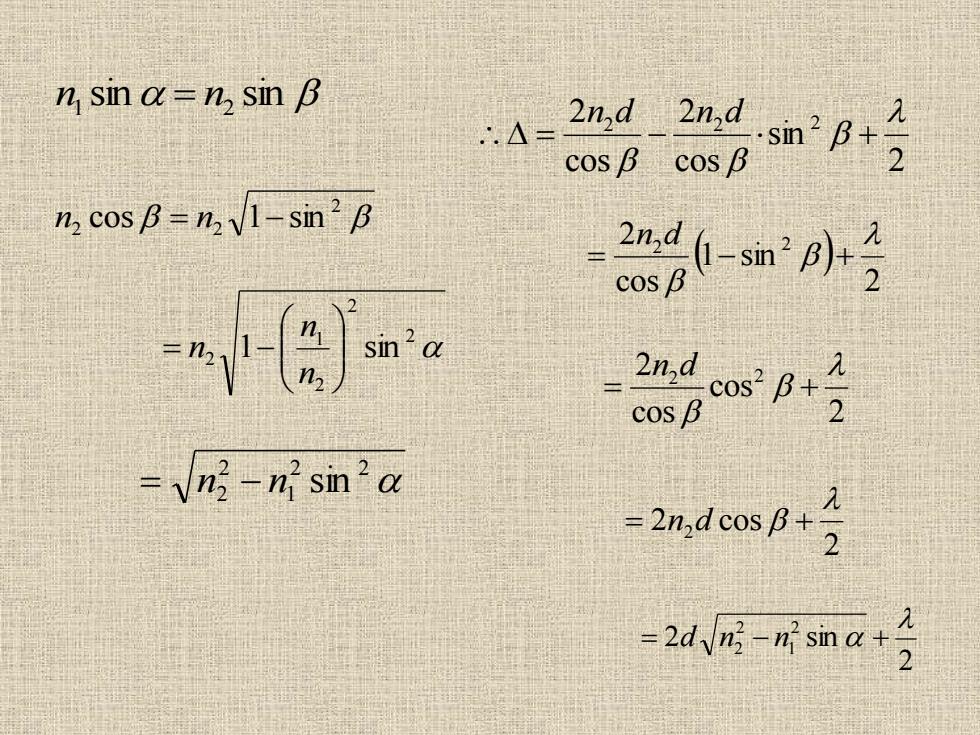
n sin a=n,sin B 4=2%d cos B cos B m2p2 2n,d n cos B=n1-sin2B -小月 sin2a -m号 =n2-n sin2a 2n.dc -2d远-sma+号
n1 sin = n2 sin 2 2 2 n cos = n 1−sin 2 2 2 1 2 1 sin = − n n n 2 2 1 2 2 = n − n sin 2 sin cos 2 cos 2 2 2 2 = − + n d n d ( ) 2 1 sin cos 2 2 2 = − + n d 2 cos cos 2 2 2 = + n d 2 2 cos 2 = n d + 2 2 sin 2 1 2 2 = d n − n +