
3、抽象数据类型树的定义 ADT TREE{ n个数据元素的集合。数据元素可以是整 型、字符型、结构类型。 数据对象: D={aa∈ElemSet,i=1,2,.,n,n≥0} 数据关系:R 想利用数学的语言正确地描述出前驱和 基本操作: 后继结点的一对多的关系不太容易;不再要 求,感兴趣的同学自己看教材。 ADT TREE
3 、 抽 象 数 据 类 型 树 的 定 义 ADT TREE{ 数据对象: D={ai | ai∈ElemSet, i=1,2,.,n, n≥0} 数据关系:R 基本操作: } ADT TREE n个数据元素的集合。数据元素可以是整 型、字符型、结构类型。 想利用数学的语言正确地描述出前驱和 后继结点的一对多的关系不太容易;不再要 求,感兴趣的同学自己看教材

关于基本操作的几点说明: 1、基本操作是定义于逻辑结构上的基本操作,向外 界提供一个与其通讯的接口。还没有用具体的某种程 序语言写出具体的算法,而算法的实现只有在存储结 构确立之后。对应于不同的存储结构,树的基本操作 的实现也不相同。 2、基本操作的种类可随实际需要的不同而不同,定 义多少种基本操作由自己确定。 3、针对不同的需要,基本操作的参数和返回值可以 有所变化
关于基本操作的几点说明: 1、基本操作是定义于逻辑结构上的基本操作,向外 界提供一个与其通讯的接口。还没有用具体的某种程 序语言写出具体的算法,而算法的实现只有在存储结 构确立之后。对应于不同的存储结构,树的基本操作 的实现也不相同。 2、基本操作的种类可随实际需要的不同而不同,定 义多少种基本操作由自己确定。 3、针对不同的需要,基本操作的参数和返回值可以 有所变化

树的基本操作: (1)Root0:求树的根结点。 (2)Parent(t):求结点t的双亲结点。 (3) Child(t,):求结点t的第i个子结点。 (4)RightSibling():求结点t第一个右边兄弟结点
树的基本操作: (1)Root():求树的根结点。 (2)Parent(t):求结点t的双亲结点。 (3)Child(t, i):求结点t的第i个子结点。 (4)RightSibling(t):求结点t第一个右边兄弟结点
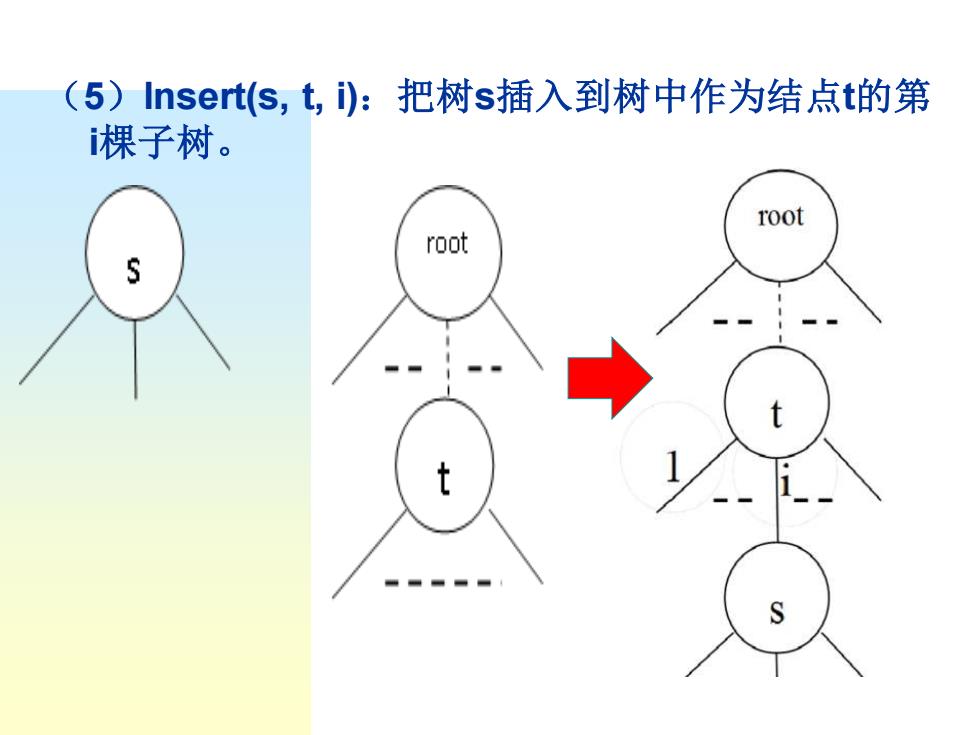
(5)nsert(s,t,):把树s插入到树中作为结点t的第 棵子树。 root root S
(5)Insert(s, t, i):把树s插入到树中作为结点t的第 i棵子树
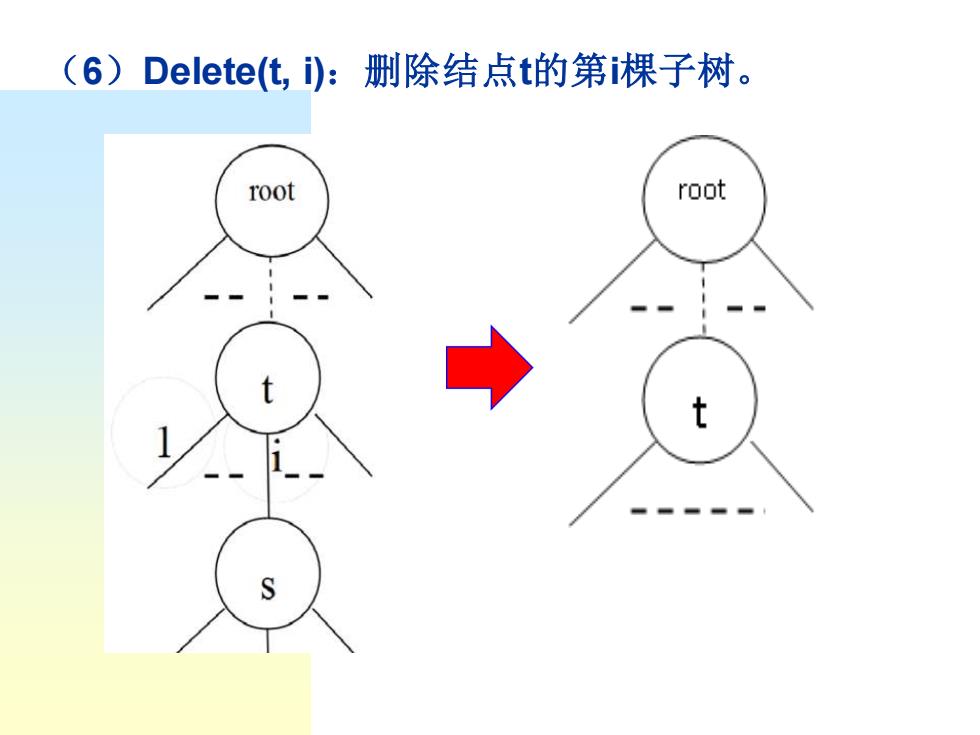
(6)Delete(ti):删除结点t的第i棵子树。 root root
(6)Delete(t, i):删除结点t的第i棵子树