
:例3.2求出下列有限长度序列的离散时间付利叶变换。 x(n)={1,2,3,4,5 解:用定义(3.1) x(e)=】 x(n)em=。+2+3e加+4e2+5e 因为X(“)是一个复值函数,必须分别画出它的模和相角(或实部和虚部)随频率仙变化 的曲线以使用图形表现它。现在ω是一个从-©到+∞的实变量,这意味着我们只能用 MATLAB出X(e)函数的一部分。利用离散时间付利叶变换的两个重要特性,可以把这 个域对实值序列缩小到[0,π]区问。我们将在下·节中讨论X()的一些其他重要特性。 两个重要特性 我们将不加F明地叙述下面两个特性。 1.周期性:离散时间付利叶变换X(e加)是w的周期函数,其周期为2π。 X(e“)=X(e[w+2x]) 推论:我I川需要X(严)的·个周期(即w∈[0,2π],或[-π,π],等等)而不需要整个 -0<w<+o域来分析。 2.对称性:对于实值的x(n),X(e")是共轭对称的。 X(e-")=X(e)) 或 Rel x(e-)]=Rel x(ef)] (偶对称) Im[X(e-")]=-Im[x(e")] (奇对称) 1X(e-m)1=IX(e") (偶对称) ∠X(e-m)=-/X(e") (奇对称) 推理:要画出X(e“),我创现在只需X(e“)半个周期。通常在实际中是选择w∈[0,π] 的部分 MATLAB实现 如果x(n)是无限长的,则不能直接用MATLAB来由x(n)计算X(e),然而我们可以 州它来估计表示式X(")在10,π]频率区间的值并且画出它的模和相角(或实部和虚部) 36
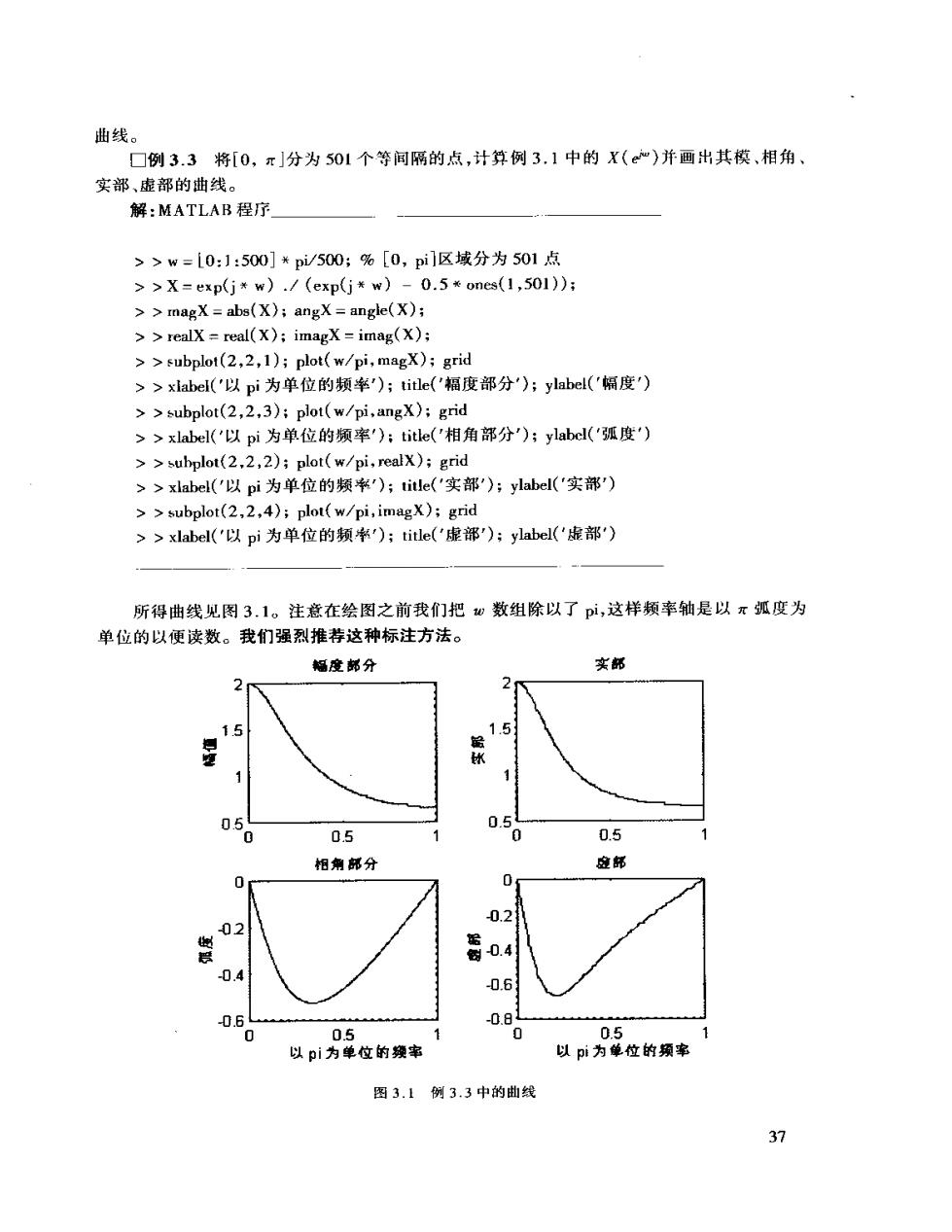
曲线。 □例3.3将[0,π]分为501个等间隔的点,计算例3.1中的X(e“)并画出其模,相角、 实部、虚部的曲线。 解:MATLAB程序 >>w=10:1:500]*pi/500;%[0,pi]区域分为501点 >>X=exp(jx w)./(exp(j*w)-0.5*ones(1,501)) >magX abs(X);angX angle(X); >realx real(X);imagX imag(X); >subplot(2,2,1);plot(w/pi,magX);grid >>xlabel(('以pi为单位的频华);title('辐度部分);ylabel('幅度') >subplot(2,2,3);plot(w/pi,angx);grid >>xlabel('以pi为单位的频率'):title('相角部分');ylabel('孤度') >subplot(2,2,2);plot(w/pi,realx);grid >>xlabel('以pi为单位的频*);title('实部);ylabel('实部) >subplot(2,2,4);plot(w/pi,imagx);grid >>xlabel('以pi为单位的频率);title('虚部');ylabel('虚部') 所得曲线见图3.1。注意在绘图之前我们把数组除以了pi,这样频率轴是以π弧度为 单位的以便读数。我们强烈推荐这种标注方法。 幅度部分 实部 2 2 15 1.5 的 0.5 0.5 0.5 0 0.5 相州部分 应部 0.2 02 需o4 -0.4 0.6 -0. -08 0 0.5 0.5 以pi为单位的频率 以p为单位的频率 图3.1例3.3中的曲线 37

果x(n)是有限长的,则可以用MATLAB来对任意频率w处的X(em)进行数值计算。 此外,如果我们是在[0,π]间按等间隔频点来估计X("),则(3.1)可以用矩阵-向量相乘的运 算米实现。为了并懂这一点,我们假定序列x(n)在n1≤n≤w(即不一定在[0,N-1间)有 个样木,而要估计下列诸点上的X(e")。 m△新k,k=0,1,,M 它们是[0,π之间的(M+1)个等间隔频点。恻(3.1)可写成: X(e)= e-jx/M)mx(),k=0,1,,M 1-1 当x(n:)和{X(e)}分别排成列向量x和X,我]有: X=Wx (3.3) 其中W是一个(M+1)乘N维矩阵如下: W△e-/w)n;n1≤n≤nN,k=0,l,,M 此外如果我」分别将{k和{,}排成列向量,则 w=exp(-j府k'n] 在MATLAB中,我们把序列和下标排成行向量,因此取(3.3)式的转置,得到: xT=x"[exp(-jnk)] (3.4) 注意nTk是一个N乘(M+1)维矩阵。于是(3.4)可用MATLAB实现如下。 >>k=[0:M];n=[n1:n2]: >>X=X*(exp(-j*pi/M))."(n'*k); ☐例3.4对例3.2中的x(n)序列的离散时间付利叫变换,在[0,π]之间的501个等间 隔獭点上进行数值计算。 解:MATLAB程序 38

>>n=-1:3;x=1:5; %x(n)序列 >>k=0:500;w=(pi/500)¥k: %L0,pi]轴分为501点。 >>X=x¥(exp(-j*pi/500).(n'k): %用矩阵-向量乘法求DTFT >magX abs(X);angX=angle(X) realx=real(X);imagX imag(X); >subplot(2.2,1);plot(R/500,magX);grid >>xlabel(以pi为单位的频*);title('幅度部分'); >subplot(2,2,3);plot(R/500,angx/p);grid >>xlabel('以pi为单位的频率');title('相角部分): >subplot(2,2,2);plot(R/500,realx);grid >>xlabel('以pi为单位的频率);itle('实部): subplot(2,2,4);plot(R/500,imagX);grid >>xlabel(以pi为单位的频率);title('虚部): 这些频域曲线见图3.2。注意相角曲线画成了一π和之间的不连续曲线,这是因为在 MATLAB中只计算主角、 幅度部分 芙都 15 15 10 10 塑 球 51 5 0 0 0.5 0 0.5 相角部分 金部 4 01 筋 .10 05 0.5 1 以p为单位的频率 以p为单位的须宰 图3.2例3.4中的曲线 上述例子中的过程可以编成-个MATLAB函数,即dtt函数,以便于执行。这在习题 3.1中探讨。这个数值计算是基于定义(3.1)的,它不是计算离散时间付利川变换的高明的方 法。此外它要产生一个N乘(M+1)的矩阵(3.4),当M和N很大时可能会超出学生版 MATLAB的存储极限。在第五章中我们将详细讨论~个可计算的变换,称为离散付利叶变换 (DFT),以及称为快速付利叶变换(FFT)高效的计算方法。另外有一种办法足基于z变换 39

的:它把MATL.AB函数feq?用于有限长序列。我们将在第四章中讨论。在本章中,将继续 用已经讨论过的方法来计算和研究。 在下两个例子中,我们将利州复值和实值序列来研究其周期性和对称性。 ☐例3.5令x(n)=(0.9exn(π3)",0≤n≤l0。求X(e")并探讨其周期性。 解:因为x()是复值的,它只满足周期性。所以它被唯一地定义在一个2π周期上 然而,我们将在「-2π,2π]之间的两个周期中的401个频点上作计算以规察其周期性。 >>n=0:10:x=(0.9*exp(j*pi/3).n; >>k=-200:200;w=(pi/100)*k; >>X=x*(exp(-jPi/100)).·(n'*k): >magX abs(X);angX anglc(X); >subplot(2,1,1);plot(w/pi,magx);grid >>xlabel('以pi为单位的频*);ylabel('IXI') >>title('幅度部分') >subplot(2,1,2);plot(w/pi,angX/pi);grid >>xlabel('以pi为单位.的频率)ylabel('孤度/pi) >>title('相角部分) 从刻3.3的曲线可以看到X(e”)对w是周期性的但不是共轭对称的。 幅度部分 ≤4 2 2 .15-1 0.5 0 0.5 115 相角部分 0.5 M 05 .15 -05 00.5 1 1.5 2 以p为单位的须率 图3.3例3.5的曲线 ☐例3.6·令x(n)=(-0.9),-5≤n≤5,讨论其离散时间付利叶变换的共轭对称性 解:我1还足计算并画出X(”)的两个周期以研究它的对称特性。 40