
五、多热源可逆循环 1.平均吸(放)热温度 q=Tds=T (s2-5) a Im= 2-S1 注意:1)Tm仅在可逆过程中有意义 2) 7m¥3+3 2 2.多热源可逆循环 h=1-鱼=1 面积1B2mml 941 面积1A2mnl =1 面积qrmng=1-<1- 面积opmn0 T T 16
16 五、多热源可逆循环 1. 平均吸(放)热温度 ( ) 2 m 2 1 1 q T s T s s = = − d 注意:1)Tm 仅在可逆过程中有意义 1 2 m 2 T T T + 2. 多热源可逆循环 2 t 1 1 2 1 1 1 1 2 1 q B mn q A mn = − = − 面积 面积 2 1 m 2 1 T sd T s s = − mL L mH H 1 1 1 qrmnq T T opmno T T = − = − − 面积 面积 2)

循环热效率归纳: 7= Wnet=1-92 适用于一切工质,任意循环 91 941 Tm放 适用于多热源可逆循环,任意工质 Tn吸 I Ta 适用于卡诺循环,概括性卡诺循环,任意工质 讨论:热效率 1
17 循环热效率归纳: net 2 t 1 1 1 w q q q = = − m m 1 T T = − 放 吸 L H 1 T T = − 讨论:热效率 适用于一切工质,任意循环 适用于多热源可逆循环,任意工质 适用于卡诺循环,概括性卡诺循环,任意工质
5-3熵和热力学第二定律的数学表达式 熵是状态参数 1.证明:任意可逆过程可用一组 初、终态相同的由可逆 绝热及等温过程组成的 b D 过程替代。 h ⑦ 如图,1-2可用1-a,-b-c及c-2代替。 E 需证明:1-a及1-b-c-2的功和热量 分别相等。 令面积B=D+F Wi-2=C+E+D Wi-a =-A Wa-c=B+A+C+E+G wc-2=-F-G 18 K
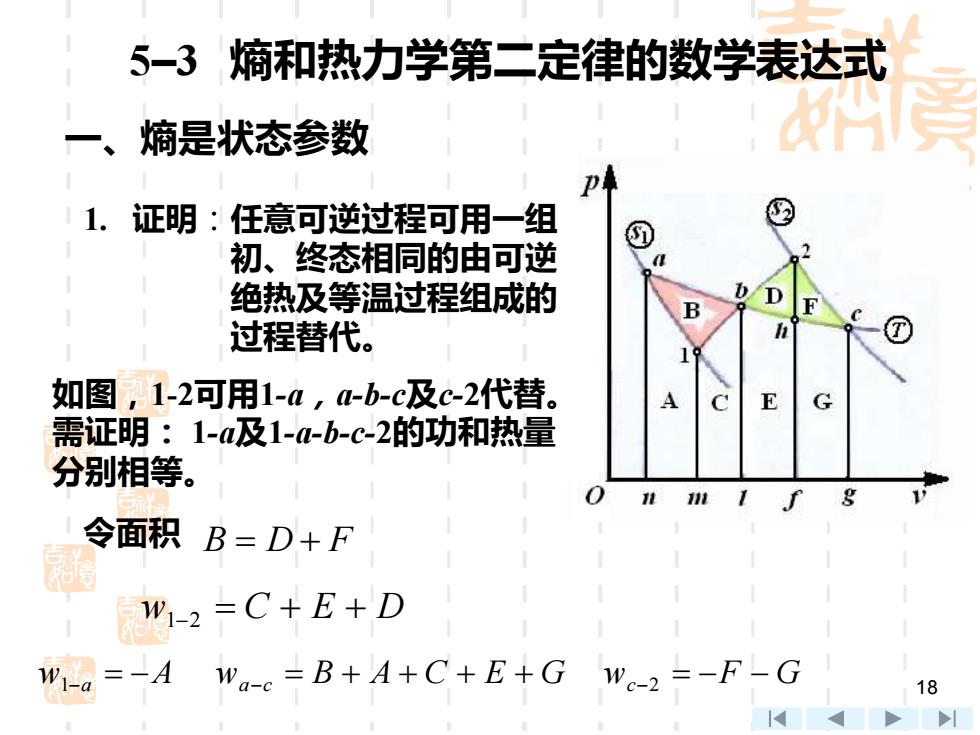
18 5–3 熵和热力学第二定律的数学表达式 一、熵是状态参数 1. 证明:任意可逆过程可用一组 初、终态相同的由可逆 绝热及等温过程组成的 过程替代。 如图,1-2可用1-a,a-b-c及c-2代替。 需证明: 1-a及1-a-b-c-2的功和热量 分别相等。 B D F = + w1−a = −A w1−2 = C + E + D wa−c = B + A + C + E + G wc−2 = −F − G 令面积

W-a-c-2 Wi-a Wa-c Wc-2 =-A+(B+A+C+E+G)-(F+G) =B+C+E-F-D+F+C+E-F =D+C+E=w1-2 又 △42=△4ac2 b B ⑦ 所以912=△412+W1-2=91-a-c-2 A E 劇 =△41ac2+M1-a-c-2 思 漫 超 19
19 w w w w 1 2 1 2 − − − − − − a c a a c c = + + 12 1 2 ac = u u = −A + (B + A + C + E + G) − ( F + G ) = B + C + E − F = D + F + C + E − F = D + C + E = w 1 − 2 12 12 1 2 1 2 a c q u w q = + = − − − − 1 2 1 2 ac a c = + u w− − − 又 所以
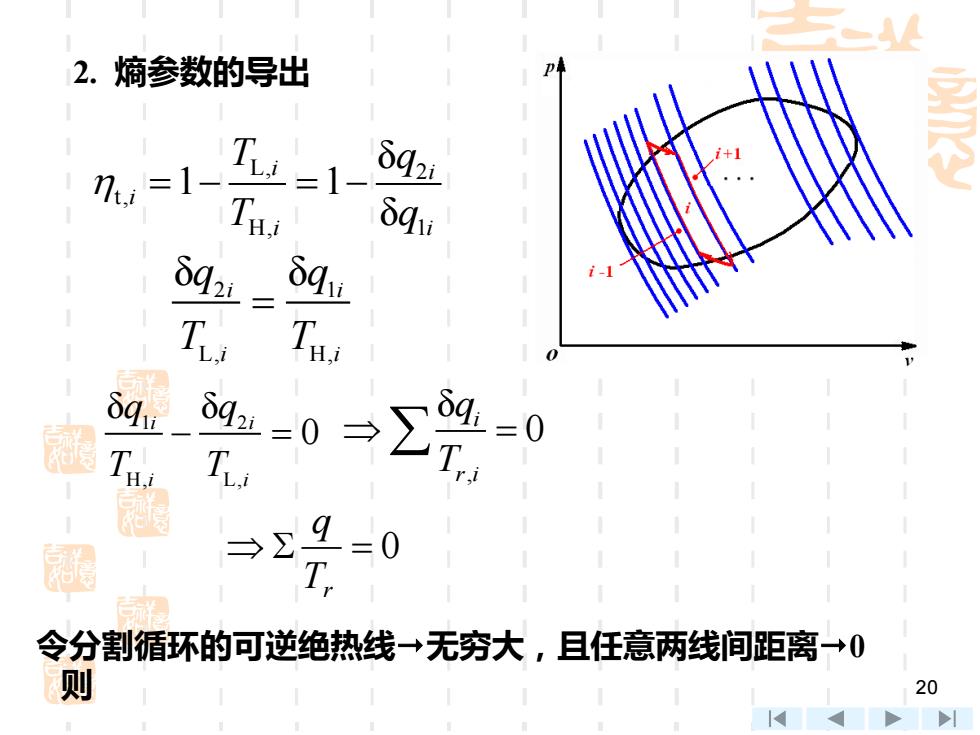
-4 2.熵参数的导出 7,=1 Tw=1- 42i Tai Squ q T T 8g4=0→g0 T 型 思 令分割循环的可逆绝热线→无穷大,且任意两线间距离→0 则 20 K >川
20 2. 熵参数的导出 L , 2 t , H, 1 δ 1 1 δ i i i i i T q T q = − = − 1 2 H, L, δ δ 0 i i i i q q T T − = 令分割循环的可逆绝热线无穷大,且任意两线间距离0 则 2 1 L, H, δ δ i i i i q q T T = , δ 0 i r i q T = = 0 Tr q