Error detection EDC:error detection and correction bits (e.g.,redundancy) D:data protected by error checking,may include header fields datagram datagram Error detection not 100% otherwise reliable! all bits in D' N ■protocol may miss K detected some errors,but rarely d data bits error larger EDC field yields D EDC D EDC' better detection and correction bit-error prone link LinkLayer:611
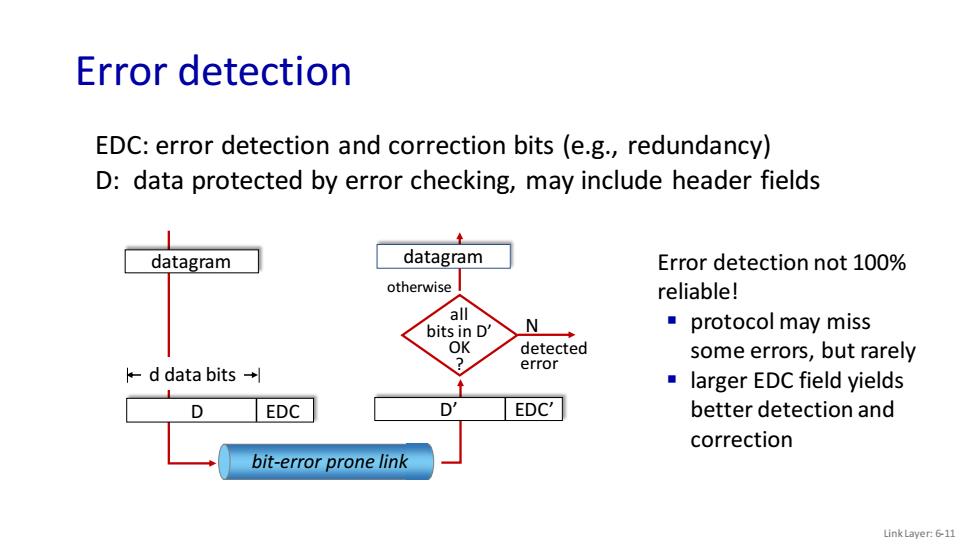
Error detection Link Layer: 6-11 EDC: error detection and correction bits (e.g., redundancy) D: data protected by error checking, may include header fields Error detection not 100% reliable! ▪ protocol may miss some errors, but rarely ▪ larger EDC field yields better detection and correction datagram D EDC d data bits bit-error prone link D’ EDC’ all bits in D’ OK ? N detected error otherwise datagram

Parity checking single bit parity: two-dimensional bit parity: detect single bit errors detect and correct single bit errors row parity 0111000110101011 d11 d —d data bits→ d21 dzj d2*1 parity bit column d du d1 parity Even parity:set parity d*11 dd bit so there is an even number of 1's no errors: 1010111 detected 101011 111100 and 011101 correctable single-bit 011101 101010 error: 101010 Check out the online interactive exercises for more panty error examples:http://gaia.cs.umass.edu/kurose_ross/interactive/ Link Layer:6-12
Parity checking Link Layer: 6-12 single bit parity: ▪ detect single bit errors 0111000110101011 1 parity bit d data bits two-dimensional bit parity: ▪ detect and correct single bit errors d1,1 d2,1 di,1 . . . d1,j+1 d2,j+1 di,j+1 . . . . . . d1,j d2,j di,j . . . di+1,1 di+1,j+1 di+1,j . . . . . . . . . . . . row parity column parity 0 1 1 1 0 1 1 0 1 0 1 1 1 1 1 1 0 0 1 0 1 0 1 0 no errors: 0 1 1 1 0 1 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 0 1 0 parity error parity error detected and correctable single-bit error: Even parity: set parity bit so there is an even number of 1’s * Check out the online interactive exercises for more examples: http://gaia.cs.umass.edu/kurose_ross/interactive/

Internet checksum(review) Goal:detect errors(i.e.,flipped bits)in transmitted segment sender: receiver: ■treat contents of UDP compute checksum of received segment (including UDP header segment fields and IP addresses)as sequence of 16-bit integers check if computed checksum equals checksum:addition (one's checksum field value: complement sum)of segment not equal-error detected content equal-no error detected.But maybe checksum value put into errors nonetheless?More later.... UDP checksum field Transport Layer:3-13
Internet checksum (review) sender: ▪ treat contents of UDP segment (including UDP header fields and IP addresses) as sequence of 16-bit integers ▪ checksum: addition (one’s complement sum) of segment content ▪ checksum value put into UDP checksum field receiver: ▪ compute checksum of received segment ▪ check if computed checksum equals checksum field value: • not equal - error detected • equal - no error detected. But maybe errors nonetheless? More later …. Goal: detect errors (i.e., flipped bits) in transmitted segment Transport Layer: 3-13

Cyclic Redundancy Check(CRC) more powerful error-detection coding D:data bits(given,think of these as a binary number) G:bit pattern (generator),of r+1 bits(given) r CRC bits d data bits D bit pattern <D,R>=D*2 XOR R formula for bit pattern goal:choose r CRC bits,R,such that <D,R>exactly divisible by G(mod 2) receiver knows G,divides <D,R>by G.If non-zero remainder:error detected! can detect all burst errors less than r+1 bits widely used in practice(Ethernet,802.11 WiFi) Link Layer:6-14
Cyclic Redundancy Check (CRC) ▪ more powerful error-detection coding ▪ D: data bits (given, think of these as a binary number) ▪ G: bit pattern (generator), of r+1 bits (given) Link Layer: 6-14 goal: choose r CRC bits, R, such that <D,R> exactly divisible by G (mod 2) • receiver knows G, divides <D,R> by G. If non-zero remainder: error detected! • can detect all burst errors less than r+1 bits • widely used in practice (Ethernet, 802.11 WiFi) r CRC bits d data bits D R <D,R> = D 2r * XOR R bit pattern formula for bit pattern

Cyclic Redundancy Check(CRC):example We want: 101011 D2r XOR R=nG 1001101110000 or equivalently: 1001 D2=nG XOR R 101 D*2r 000 or equivalently: 1010 1001 if we divide D2r by G,want 110 remainder R to satisfy: 000 R=remainder D21 1100 1001 1010 1001 011 R Check out the online interactive exercises for more examples:http:/gaia.cs.umass.edu/kurose_ross/interactive/ Link Layer:6-15
Link Layer: 6-15 Cyclic Redundancy Check (CRC): example We want: D.2 r XOR R = nG * Check out the online interactive exercises for more examples: http://gaia.cs.umass.edu/kurose_ross/interactive/ D.2 r G R = remainder [ ] or equivalently: D.2 r = nG XOR R or equivalently: if we divide D.2 r by G, want remainder R to satisfy: 1 0 0 1 1 0 1 0 1 0 1 0 0 0 1 0 0 1 1 0 0 1 1 0 0 1 0 0 0 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 D R 1 0 0 1 G 1 0 1 1 1 0 0 0 0 2 r * 1 0 1