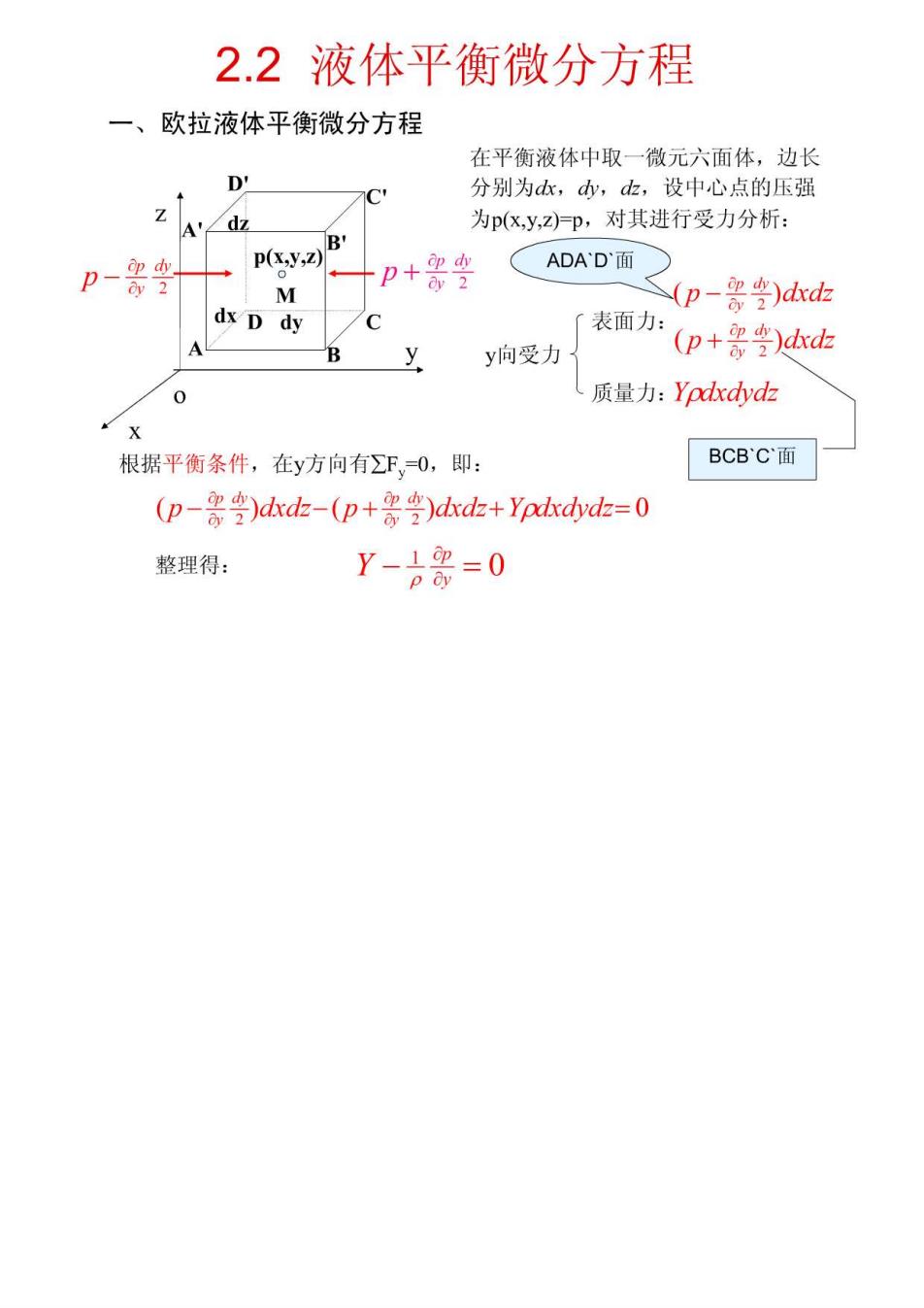
2.2液体平衡微分方程 一、欧拉液体平衡微分方程 在平衡液体中取一微元六面体,边长 D' 21 分别为k,,d,设中心点的压强 ∠d 为(xy,z)p,对其进行受力分析: p-等 p(xy.z)B' ADAD面) M (p-要g)dkdk dx D dy 表面力: B y y向受力 (p+要安)dkdb 0 质量力:Ypdxdvdz 根据平衡条件,在y方向有∑F,O,即: BCBC面 (p-等)kdt-(p+票)dkdt+Ypddyd=0 整理得: Y-2票=0

同理,对x、z方向可得出类似结果,从而得到液体平衡微分 方程(即欧拉平衡方程): X-器=0 px= Y-÷器=0 或写成 pY=in Z-b器=0 pZ=器 物理意义:处于平衡状态的液体,压强沿坐标轴向的变化 率等于该轴向单位体积上的质量力的分量(pX,PY,PZ)。 2x-普xnx2兰2

将欧拉平衡微分方程式各式分别乘以dx,dy,dz,然后相加得: dr+卫dy+pd=p(x+t+zd) Ox 上式是不可压缩均质液体平衡微分方程式的另一种表达形式。 显然上式左端为静水压强函数p(K,y,z)的全微分dp,于是 Op dx+dy+Odz=dp=p(Xdx+rdy+Zdz) 上式是不可压缩均质液体平衡微分方程式的另一种表达形式

第二章水静力学 二、力势函数及液体平衡微分方程式的积分 将欧拉方程前两式分别对y和x取偏导数,液体密度为常数。 ap=dpx_lpl→ax_y pX=器 pY=哥 pZ=器 同理可得 8X 8y 0x 由理论力学知, X=OW 满足左边各式必 oy oz 然存在力势函数 0z Y=ow oZ =x W(x,y,z)有 Ox 2 0z

对右式分别乘以dx、dy、dz后相加得 r=O形 dr+ow ow Ox dro Ox -dz=Xdx+Ydy+Zdz Y=ow 上式左端是力势函数的全微分,且等于单位质 量力在空间移动距离所作的功,即 &z aw dy* ow -dz=Xdx+Ydy+Zdz 上式表明:作用在液体上的质量力必是有势力液体才能 保持平衡 故有dp=pWdr+0 d+0 -dz)=pdw 备4EXT