
圆轴扭转时的内力计算举例 m 解: (a) m,=70244=1170Nw n mn. ma=7024V2=351Mn (b) (d). n (c) m:=7024V2=351Nwm mc Tu n 468N.m m。=7024VD=468Nm n e 351N.m 702N.m
解: Nm n N m D D = 7024 = 468Nm n N m B C = 7024 = 351 圆轴扭转时的内力计算举例 Nm n N m A A = 7024 =1170Nm n N m B B = 7024 = 351
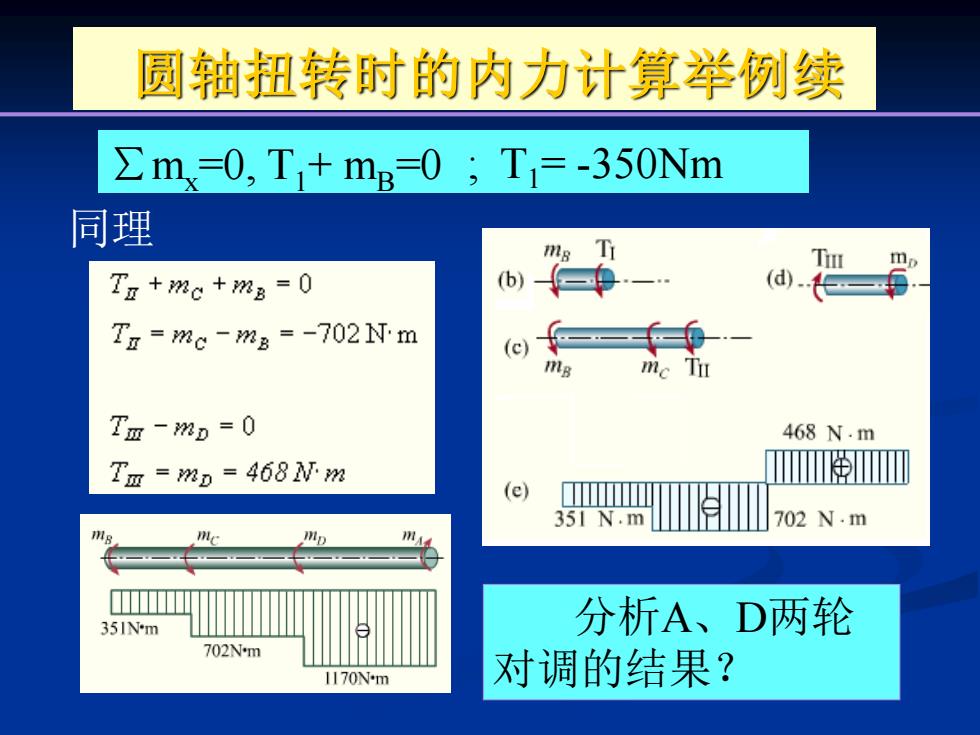
圆轴扭转时的内力计算举例续 ∑m0,T1+mε=0;T1=-350Nm 同理 T m Tn +mc+mg =0 (b) T =mc -m8 =-702N'm (c) Tm-mD=0 468N.m Tm=nD=468N为 (e) 351N.m 702N.m 用4 351Nm 分析A、D两轮 702Nm 1170Nm 对调的结果?
∑mx=0, T1+ mB=0 ; T1= -350Nm 同理 圆轴扭转时的内力计算举例续 分析A、D两轮 对调的结果?

第9-1节 扭转Torsion 扭转切应力 扭转切应力分析 0 1、圆轴扭转时的应力和变形特征 0 2、圆轴扭转时横截面上的切应力分析 口3、矩形截面杆扭转切应力公式
1、圆轴扭转时的应力和变形特征 2、圆轴扭转时横截面上的切应力分析 3、矩形截面杆扭转切应力公式 第9-1节 扭转 Torsion 扭转切应力 扭转切应力分析
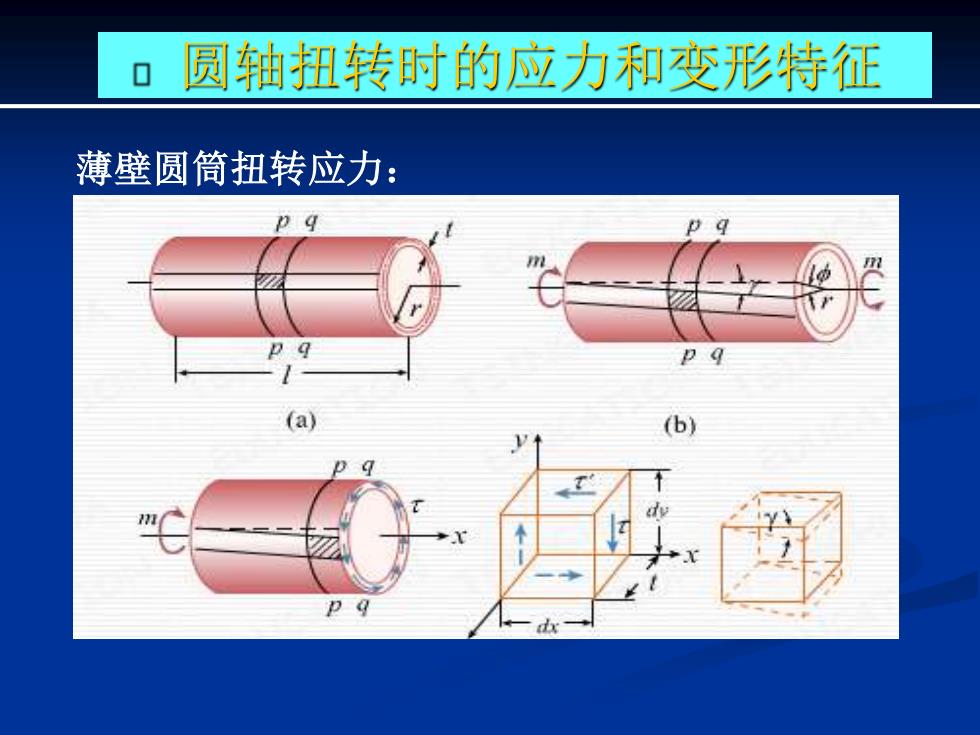
圆轴扭转时的应力和变形特征 薄壁圆筒扭转应力: p q a
圆轴扭转时的应力和变形特征 薄壁圆筒扭转应力:

圆轴扭转时的应力变形特征 扭转后相邻圆周线绕轴线相对转过一微 小转角,纵线均倾斜一微小倾角Y从而使 方格变成菱形,但圆筒沿轴线及圆周线 的形状和长度都没有变化。 。横截面没有正应力,只有切于截面 的剪应力。一纯剪切
圆轴扭转时的应力变形特征 ◼ 扭转后相邻圆周线绕轴线相对转过一微 小转角,纵线均倾斜一微小倾角从而使 方格变成菱形,但圆筒沿轴线及圆周线 的形状和长度都没有变化。 • 横截面没有正应力,只有切于截面 的剪应力。— 纯剪切