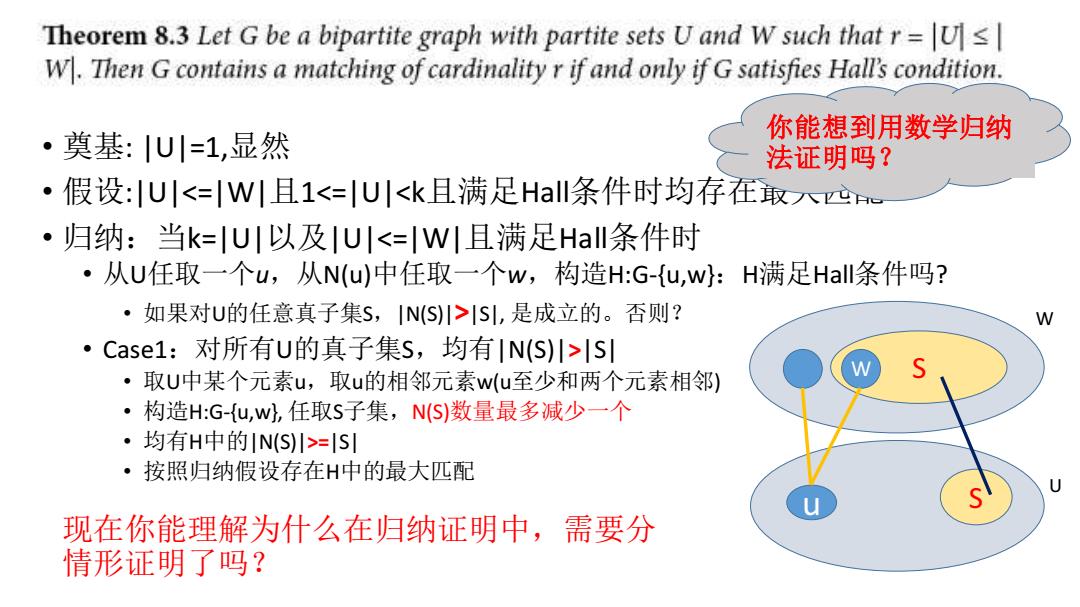
Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=U W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. ·奠基:U川=1,显然 你能想到用数学归纳 法证明吗? ·假设:U川<=|W|且1<=|U川<k且满足Hall条件时均存在取八心e ·归纳:当k=U川以及U|<=WI且满足Hall条件时 ·从U任取一个u,从N(u)中任取一个w,构造H:G-{u,w:H满足Ha条件吗? ·如果对U的任意真子集S,IN(S川>ISL,是成立的。否则? W ·Case1:对所有U的真子集S,均有|N(S)川>SI ·取U中某个元素u,取u的相邻元素w(u至少和两个元素相邻) ·构造H:G-u,w,任取S子集,N(S)数量最多减少一个 ·均有H中的IN(S)川>=|S ·按照归纳假设存在H中的最大匹配 现在你能理解为什么在归纳证明中,需要分 情形证明了吗?
U W S u S W • 奠基: |U|=1,显然 • 假设:|U|<=|W|且1<=|U|<k且满足Hall条件时均存在最大匹配 • 归纳:当k=|U|以及|U|<=|W|且满足Hall条件时 • 从U任取一个u,从N(u)中任取一个w,构造H:G-{u,w}:H满足Hall条件吗? • 如果对U的任意真子集S,|N(S)|>|S|, 是成立的。否则? • Case1:对所有U的真子集S,均有|N(S)|>|S| • 取U中某个元素u,取u的相邻元素w(u至少和两个元素相邻) • 构造H:G-{u,w}, 任取S子集,N(S)数量最多减少一个 • 均有H中的|N(S)|>=|S| • 按照归纳假设存在H中的最大匹配 你能想到用数学归纳 法证明吗? 现在你能理解为什么在归纳证明中,需要分 情形证明了吗?
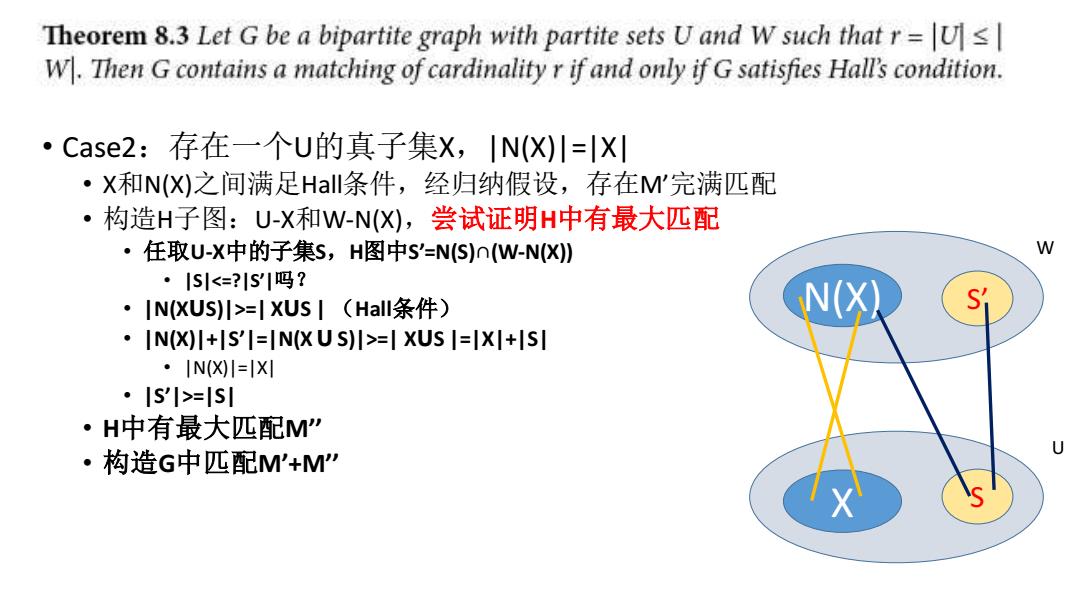
Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. ·Case2:存在一个U的真子集X,IN(X)川=X ·X和N()之间满足Hal条件,经归纳假设,存在W完满匹配 ·构造H子图:U-X和W-N(X),尝试证明H中有最大匹配 ·任取U-X中的子集s,H图中s'=NS)n(W-N() W ·1S1<=?1S1吗? ·IN(XUsl>=|XUs|(Hall条件) N() Si .IN(X)I+S'I=IN(XUS)I>=I XUS I=IXI+SI IN(X)I=|X刈 ·IsI>=lsl ·H中有最大匹配M” U ·构造G中匹配M'+
• Case2:存在一个U的真子集X,|N(X)|=|X| • X和N(X)之间满足Hall条件,经归纳假设,存在M’完满匹配 • 构造H子图:U-X和W-N(X),尝试证明H中有最大匹配 • 任取U-X中的子集S,H图中S’=N(S)∩(W-N(X)) • |S|<=?|S’|吗? • |N(XꓴS)|>=| XꓴS | (Hall条件) • |N(X)|+|S’|=|N(X ꓴ S)|>=| XꓴS |=|X|+|S| • |N(X)|=|X| • |S’|>=|S| • H中有最大匹配M’’ • 构造G中匹配M’+M’’ U W X N(X) S S’

这个定理的直观含义是什么? Theorem 8.4 A collection [S,S2,...S of nonempty finite sets has a system of distinct representatives if and only if for each integer k with 1 sksn,the union of any k of these sets contains at least k elements. For example,consider the sets S,S2,....S,where S1={1,2,3}S2={2,4,6} S3={3,4,5} S4={1,4,7} S5={1,5,6} S6={3,6,7} S7={2,5,7} Then this collection of sets has a system of distinct representatives.In particular,1,2,..., 7(that is,iS;for i=1,2,...,7)is a system of distinct representatives.On the other hand,the sets2where S1={1,3,5,6} S%={3,4 Sg={4,5} S4={3,4,5} Sg={1,2,4,6}S%={3,5} do not have a system of distinct representatives as S2U{3,4,5 so distinct representatives do not exist for the sets
这个定理的直观含义是什么?
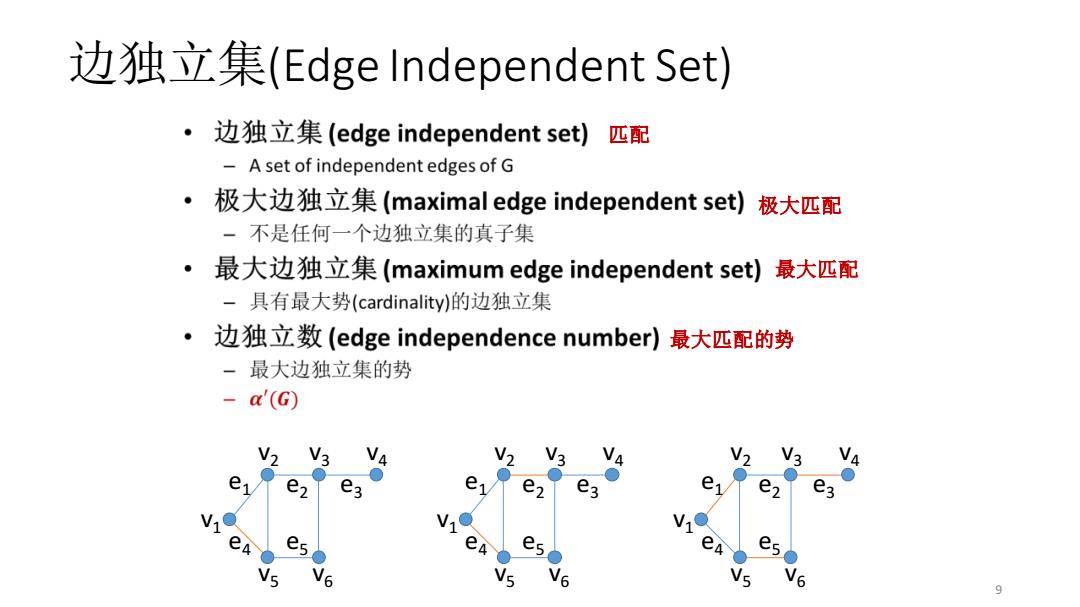
边独立集(Edge Independent Set) ·边独立集(edge independent set)I 匹配 A set of independent edges of G · 极大边独立集(maximal edge independent set)极大匹配 一不是任何一个边独立集的真子集 ·最大边独立集(maximum edge independent set)最大匹配 -具有最大势(cardinality)的边独立集 · 边独立数(edge independence number)最大匹配的势 一最大边独立集的势 -a'(G) V> e e, e e V e V6 9
边独立集(Edge Independent Set) 9 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 匹配 极大匹配 最大匹配 最大匹配的势
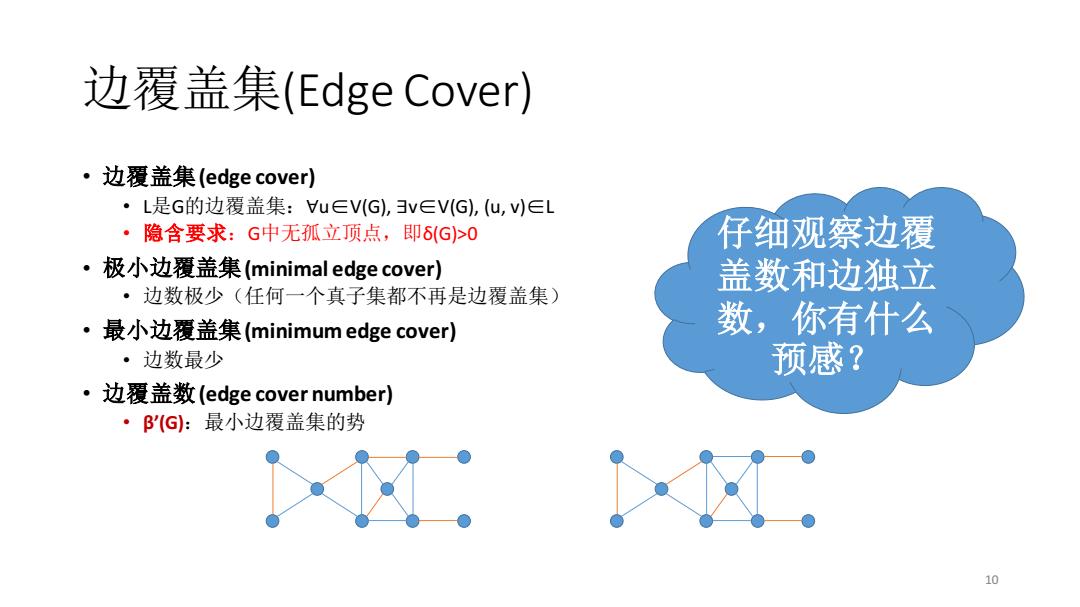
边覆盖集(Edge Cover) ·边覆盖集(edge cover) ·L是G的边覆盖集:u∈V(G),v∈V(G),(u,v)∈L ·隐含要求:G中无孤立顶点,即6(G>0 仔细观察边覆 ·极小边覆盖集(minimal edge cover) 盖数和边独立 ·边数极少(任何一个真子集都不再是边覆盖集) ·最小边覆盖集(minimum edge cover) 数,你有什么 ·边数最少 预感? ·边覆盖数(edge cover number) ·'(G:最小边覆盖集的势 10
边覆盖集(Edge Cover) • 边覆盖集(edge cover) • L是G的边覆盖集:∀u∈V(G), ∃v∈V(G), (u, v)∈L • 隐含要求:G中无孤立顶点,即δ(G)>0 • 极小边覆盖集(minimal edge cover) • 边数极少(任何一个真子集都不再是边覆盖集) • 最小边覆盖集(minimum edge cover) • 边数最少 • 边覆盖数(edge cover number) • β’(G):最小边覆盖集的势 10 仔细观察边覆 盖数和边独立 数,你有什么 预感?