
电动势定义为把单位正电荷从负极通过电源内部移 到正极的过程中,非静电力做的功在动生电动势的 情形中,作用在单位正电荷上的非静电力E是洛仑 兹力,即 E.= -vxB -e 所以,动生电动势 cw=Edi=∫(xBd 首页上页下页退出
首 页 上 页 下 页 退 出 16 电动势定义为把单位正电荷从负极通过电源内部移 到正极的过程中,非静电力做的功.在动生电动势的 情形中,作用在单位正电荷上的非静电力Ek是洛仑 兹力,即 所以,动生电动势 k f E v B e = = − ( ) b k ab a E dl v B dl + − = =

一般而言,在任意的稳恒磁场中,一个任意形状的 导线L(闭合的或不闭合的)在运动或发生形变时,各 个线元d的速度v的大小和方向都可能不同这时, 在整个线圈L中所产生的动生电动势为 &=∫(×B-di 在运动导体中自由电子不但具有导体本身的运动速 度y,而且还具有相对于导体的定向运动速度,如 图10.5所示,于是,自由电子所受到的总洛仑兹力为 F=-e(u+v)xB-euxB-evxB=f+f 首页上页下页退出
首 页 上 页 下 页 退 出 17 一般而言,在任意的稳恒磁场中,一个任意形状的 导线L(闭合的或不闭合的)在运动或发生形变时,各 个线元dl的速度v的大小和方向都可能不同.这时, 在整个线圈L中所产生的动生电动势为 在运动导体中自由电子不但具有导体本身的运动速 度v,而且还具有相对于导体的定向运动速度u,如 图10.5所示.于是,自由电子所受到的总洛仑兹力为 ( ) L = v B dl ' F e u v B eu B ev B f f = − + = − − = + ( )

这个力F与合速度V=u+的点乘为功率,即 P=F.f=(f+f)-(i+) =了u+fv =+evBu-euBv=0 图10.5洛仑兹力不做功 所以,实际上F⊥V,即总洛仑兹力对电子不做功 首页上页下页退出
首 页 上 页 下 页 退 出 18 这个力F与合速度V=u+v的点乘为功率,即 所以,实际上F⊥V,即总洛仑兹力对电子不做功. ' ' ( ) ( ) 0 P F V f f u v f u f v evBu euBv = = + + = + = + − = 图10.5 洛仑兹力不做功

然而,为使导体棒保持速度为的匀速运动,必须施 加外力f以克服洛仑滋力的一个分力f=一eum×B.利 用上式一fv=fu的结果可以看到,外力克服f做功 的功率为fv=一fv=fu.这就是说,外力克服洛仑 兹力的一个分量f所做的功的功率f等于通过洛仑 兹力的另一个分量对电子的定向运动做正功的功率 f,从而外力做的功全部转化为感应电流的能量 洛仑兹力起到了能量转化的传递作用,但前提是运 动导体中必须有能自由移动的电荷。 首页上页下页退出
首 页 上 页 下 页 退 出 19 然而,为使导体棒保持速度为v的匀速运动,必须施 加外力f 0以克服洛仑兹力的一个分力f′=-eu×B.利 用上式-f′·v=f·u的结果可以看到,外力克服f′做功 的功率为f 0·v=-f′·v=f·u.这就是说,外力克服洛仑 兹力的一个分量f′所做的功的功率f 0·v等于通过洛仑 兹力的另一个分量f对电子的定向运动做正功的功率 f·u,从而外力做的功全部转化为感应电流的能量. 洛仑兹力起到了能量转化的传递作用,但前提是运 动导体中必须有能自由移动的电荷
例10.4电流为的长直载流 导线近旁有一与之共面的导 体ab,长为l.设导体的a端与 长导线相距为d,ab延长线与 长导线的夹角为0,如图10.7 所示.导体b以匀速度沿电 流方向平移试求ab上的感应 图10.7 电动势. 解在ab上取一线元dl,它与长直导线的距离为r, 则该处磁场方向垂直向里,大小为B=,×B的 方向与d方向之间夹角为”+0,且dl sin 20 首页上页下页退出
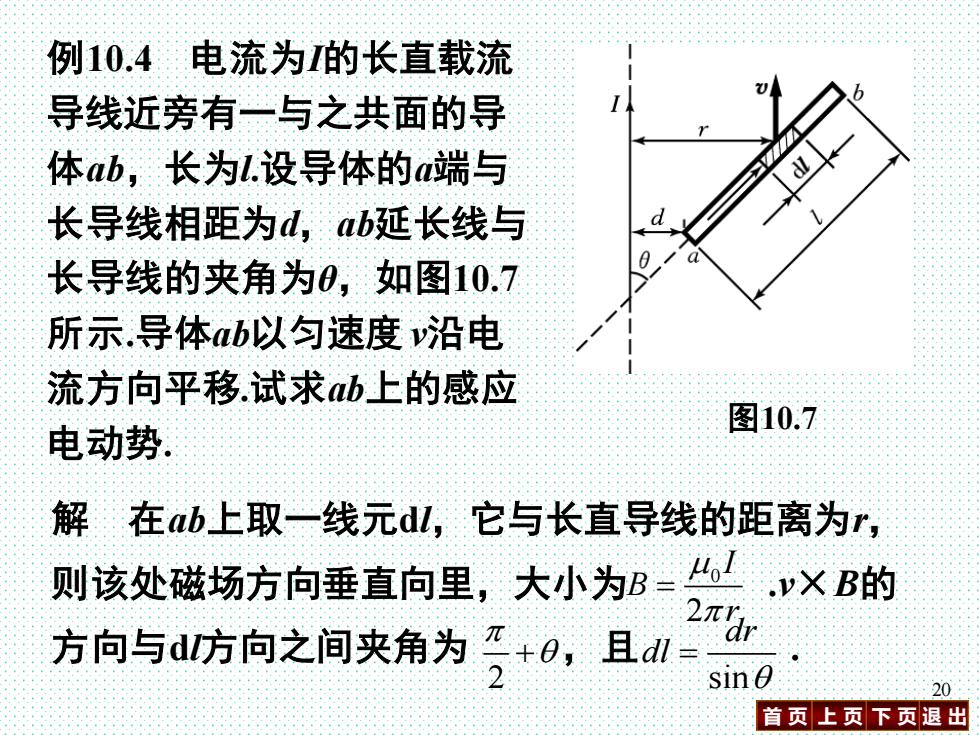
首 页 上 页 下 页 退 出 20 例10.4 电流为I的长直载流 导线近旁有一与之共面的导 体ab,长为l.设导体的a端与 长导线相距为d,ab延长线与 长导线的夹角为θ,如图10.7 所示.导体ab以匀速度 v沿电 流方向平移.试求ab上的感应 电动势. 图10.7 解 在ab上取一线元dl,它与长直导线的距离为r, 则该处磁场方向垂直向里,大小为 .v×B的 方向与dl方向之间夹角为 ,且 . 0 2 I B r = 2 + sin dr dl =