
归一化阻抗表达式, Zineino-I 1-yineyino Si-5nm+1(y(ym) Zine-Zino Yino-Yine S21-52(m1(m+1(+ym)(1+yma)
归一化阻抗表达式
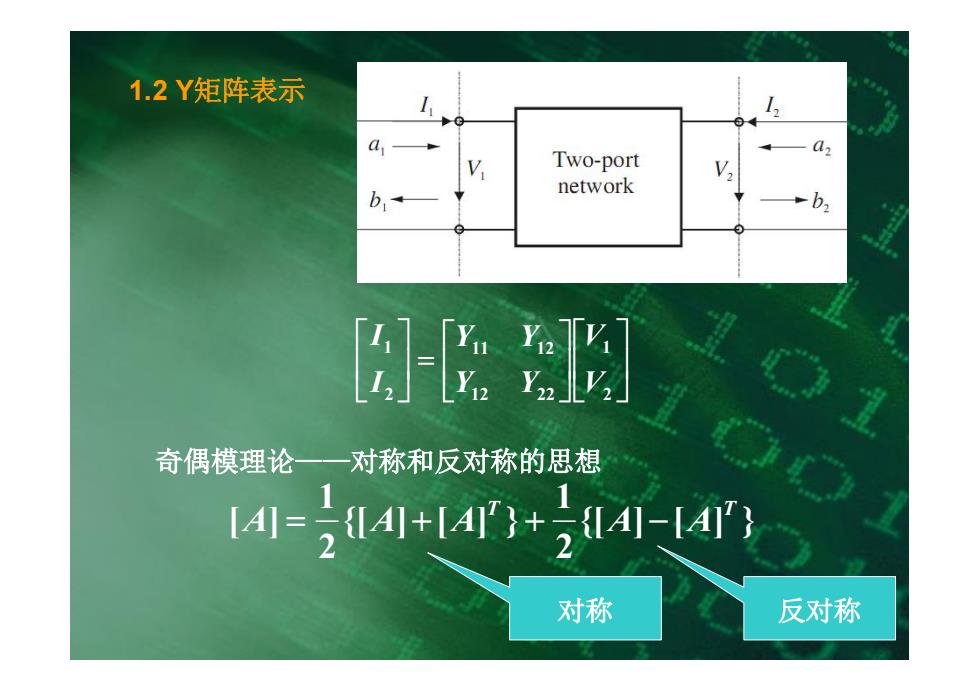
1.2Y矩阵表示 a Two-port network b14 b 时 奇偶模理论一一对称和反对称的思想 14=24+A+4-) 对称 反对称
ú û ù ê ë é ú û ù ê ë é ú = û ù ê ë é 2 1 12 22 11 12 2 1 V V Y Y Y Y I I 奇偶模理论——对称和反对称的思想 {[ ] [ ] } 2 1 {[ ] [ ] } 2 1 [ ] T T A = A + A + A - A 对称 反对称 1.2 Y矩阵表示

北北e -北+g) 称为偶模激励 北-5) 称为奇模激励 其都建立在“线性叠加原理”基础上。又记做 =2-)1,=201
( ) ú û ù ê ë é - - - ú + û ù ê ë é + + ú = û ù ê ë é 1 2 1 2 1 2 1 2 2 1 2 1 2 1 V V V V V V V V V V 令 ( ) 1 2 2 1 Ve = V +V 称为偶模激励 ( ) 1 2 2 1 Vo = V -V 称为奇模激励 其都建立在“线性叠加原理”基础上。又记做 ( ) 2 1 ( ) 2 1 ( ) 2 1 ( ) 2 1 1 2 1 2 1 2 1 2 V V V I I I V V V I I I o o e e = - = - = + = +

进一步得到 小-北最 时 再考虑对称 Y=Y22
进一步得到 ú û ù ê ë é ú û ù ê ë é - ú û ù ê ë é ú û ù ê ë é - = ú û ù ê ë é ú û ù ê ë é ú û ù ê ë é - ú = û ù ê ë é ú û ù ê ë é - ú = û ù ê ë é 12 22 0 11 12 2 1 12 22 11 12 2 1 0 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 2 1 V V Y Y Y Y V V Y Y Y Y I I I I e e ú û ù ê ë é ú û ù ê ë é - + - + + - ú = û ù ê ë é 11 22 11 22 12 0 11 22 12 11 22 0 2 2 2 1 V V Y Y Y Y Y Y Y Y Y Y I Ie e 再考虑对称 ú û ù ê ë é ú û ù ê ë é - + ú = û ù ê ë é 11 12 0 11 12 0 0 0 V V Y Y Y Y I Ie e Y11 = Y22

偶棋激励和奇模激励时,非对角元素为零,无耦合,沙 方程改写为 6 其中, Yoe=Yu+Y12 Y =Yn-Yu
ú û ù ê ë é ú û ù ê ë é - + ú = û ù ê ë é 11 12 0 11 12 0 0 0 V V Y Y Y Y I Ie e 偶模激励和奇模激励时,非对角元素为零,无耦合; ú û ù ê ë é ú û ù ê ë é ú = û ù ê ë é o e o e o e V V Y Y I I 0 0 0 0 方程改写为 其中, î í ì = = o o o e e e I Y V I Y V 0 0 0 11 12 0 11 12 î í ì = - = + Y Y Y Y Y Y o e