
a-(+@,)+(@,-@,)c0s2a -g(a-0;)sin 2a 以上0,与01,03可用莫尔圆表示,如下图。 2a dscosa
,与1 , 3 如下图。 ( ) ( ) ( ) = − = + + − sin 2 2 1 cos 2 2 1 2 1 1 3 1 3 1 3 以上 可用莫尔圆表示

(二)、土的极限平衡条件的建立 如果给定了土的抗剪强度参数φ和c以及土中某点的应力 状态,则可将抗剪强度包线与莫尔应力圆画在同一张坐标图上。 它们之间的关系有三种情况: (1)莫尔圆位于抗剪强度包线下方(圆1),说明该点在任何 平面上的剪应力都小于土所能发挥的抗剪强度 t<tf 因此不会发生剪切破坏; (2)圆3实际上不存在; (3)圆2,说明在A点所代 表的平面上剪应力正好等于 抗剪强度t=T,该点 处于极限平衡状态
(二)、土的极限平衡条件的建立 如果给定了土的抗剪强度参数和c以及土中某点的应力 状态,则可将抗剪强度包线与莫尔应力圆画在同一张坐标图上。 它们之间的关系有三种情况: (1)莫尔圆位于抗剪强度包线下方(圆1),说明该点在任何 平面上的剪应力都小于土所能发挥的抗剪强度 , 因此不会发生剪切破坏; (2)圆3实际上不存在; (3)圆2,说明在A点所代 表的平面上剪应力正好等于 抗剪强度 ,该点 处于极限平衡状态。 f f = c
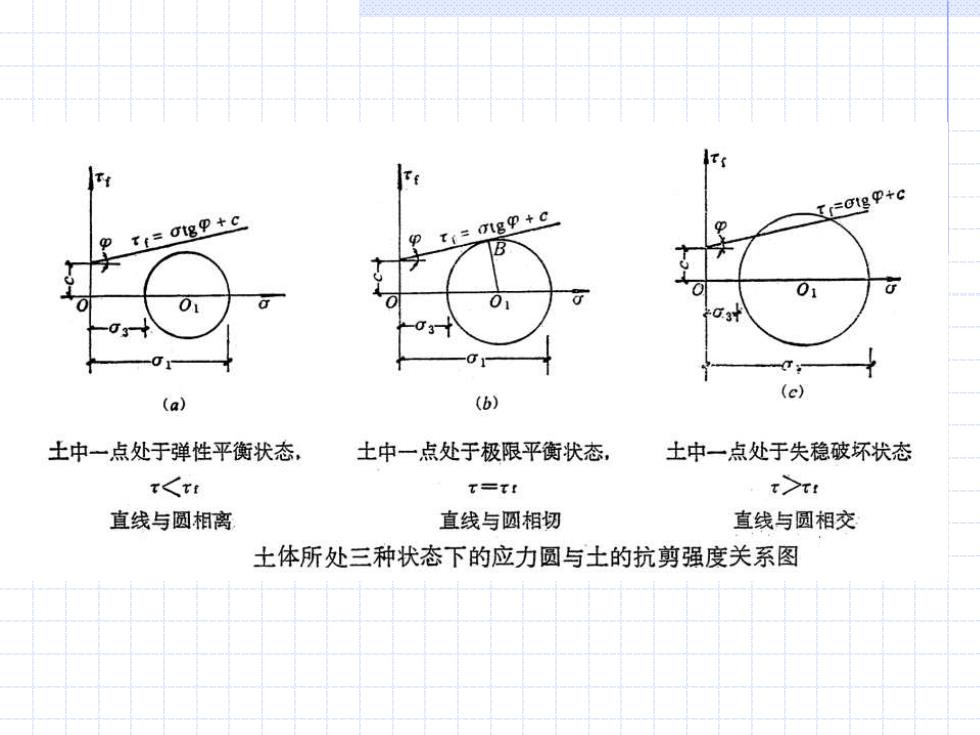
(=八gp+C Tr=+c Ti=Otgp+c 0 0 0 (b) (c) (a) 土中一点处于弹性平衡状态, 土中一点处于极限平衡状态, 土中一点处于失稳破坏状态 T<Tr T=tI 1> 直线与圆相离 直线与圆相切 直线与圆相交 士体所处三种状态下的应力圆与土的抗剪强度关系图

土处于极限平衡状态下时 根据极限应力圆与 抗剪强度包线相切 的几何关系,可建 立以下极限平衡条 c.coto- 件: 5(01+03) 号o-o=6coo+2oto,l小mw
土处于极限平衡状态下时 根据极限应力圆与 抗剪强度包线相切 的几何关系,可建 立以下极限平衡条 件: ( ) ( ) sin 2 1 cot 2 1 1 3 1 3 − = c + +

化简后得: 粘性士: 01 =o;tan2 5+号 +2ctan 45°+ o;=o;tan2 -2ctan 又s2 无粘性土: o1=o;tan2 ① 03=( o tan2 45- 2
− − = − + + = + 2 2 tan 45 2 tan 45 2 2 tan 45 2 tan 45 2 3 1 2 1 3 c c 粘性土: 化简后得: 无粘性土: = − = + 2 tan 45 2 tan 45 2 3 1 2 1 3