
3)弹簧振子的运动微分方程 以振子为对象由牛顿定律: d -kx 令0-k 则得 m 解微分方程得: x=Acos(ot+o) 6 首页上页下页退出
首 页 上 页 下 页 退 出 6 3)弹簧振子的运动微分方程 m k = 2 令 0 2 2 2 + x = dt d x 则得 kx dt d x m = − 2 2 以振子为对象 由牛顿定律: cos( ) = +0 解微分方程得: x A t
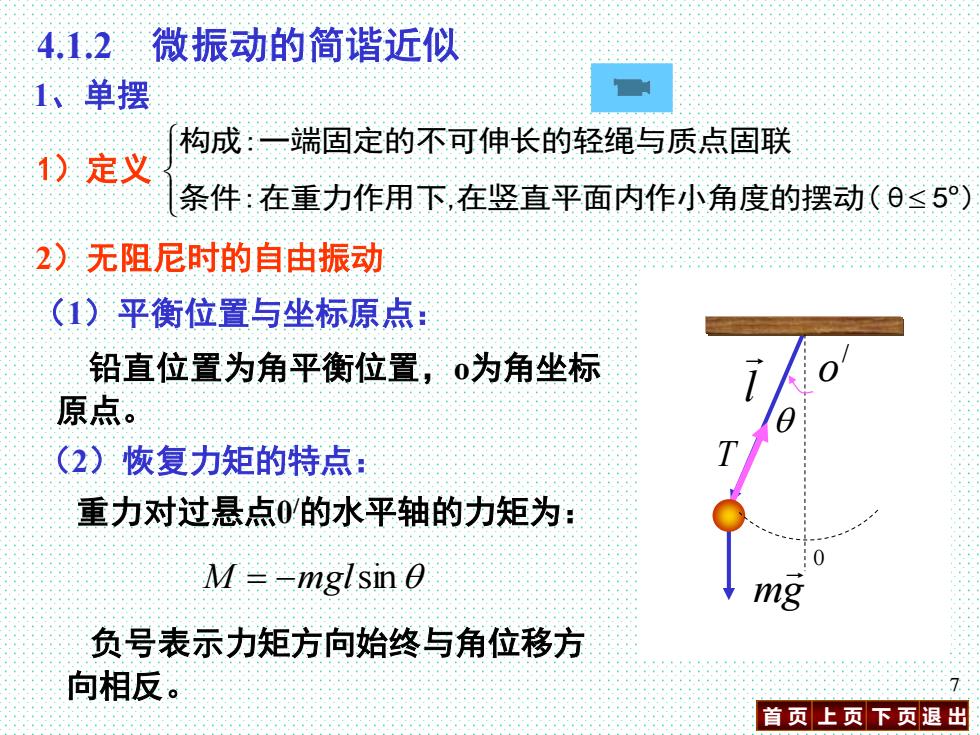
4.1.2 微振动的简谐近似 1、单摆 构成:一端固定的不可伸长的轻绳与质点固联 1)定义 条件:在重力作用下,在竖直平面内作小角度的摆动(≤5°) 2)无阻尼时的自由振动 (1)平衡位置与坐标原点: 铅直位置为角平衡位置,0为角坐标 原点。 (2)恢复力矩的特点: 重力对过悬点0的水平轴的力矩为: M=-mglsin 0 mg 负号表示力矩方向始终与角位移方 向相反。 首页上页下页退出
首 页 上 页 下 页 退 出 7 2)无阻尼时的自由振动 (1)平衡位置与坐标原点: 铅直位置为角平衡位置,o为角坐标 原点。 (2)恢复力矩的特点: 重力对过悬点0 /的水平轴的力矩为: M = −mglsin 负号表示力矩方向始终与角位移方 向相反。 1)定义 条件:在重力作用下,在竖直平面内作小角度的摆动(θ 5 ) 构成:一端固定的不可伸长的轻绳与质点固联 o 1、单摆 / o 0 l mg T / o 0 4.1.2 微振动的简谐近似

报据支克劳林层开m00}00 略去高阶无穷小后 M=-mgl.0 即恢复力矩与角位移正比而反向。 (角位移指偏离平衡位置的角位移) (3)惯性的作用: 此处的惯性指摆球对过0的水平轴的转动惯量 I =ml2 8 首页上页下页退出
首 页 上 页 下 页 退 出 8 根据麦克劳林展开 = − 3 + 5 − 5! 1 3! 1 sin 略去高阶无穷小后 M = −mgl (3)惯性的作用: 即恢复力矩与角位移正比而反向。 (角位移指偏离平衡位置的角位移) 此处的惯性指摆球对过0 /的水平轴的转动惯量 I = ml 2

3)单摆的运动微分方程 由定轴转动的转动定律: M=IB do d =-mgl.0 。-号 令 则得 d'o d +o20=0 方程的解为 日=日cos(ot+φ) 9 首页上页下页退出
首 页 上 页 下 页 退 出 9 3)单摆的运动微分方程 由定轴转动的转动定律: = −mgl dt d ml 2 2 2 令 2 = g l 0 2 2 2 + = dt d 则得 方程的解为 ( ) 0 0 = cos t + M = I
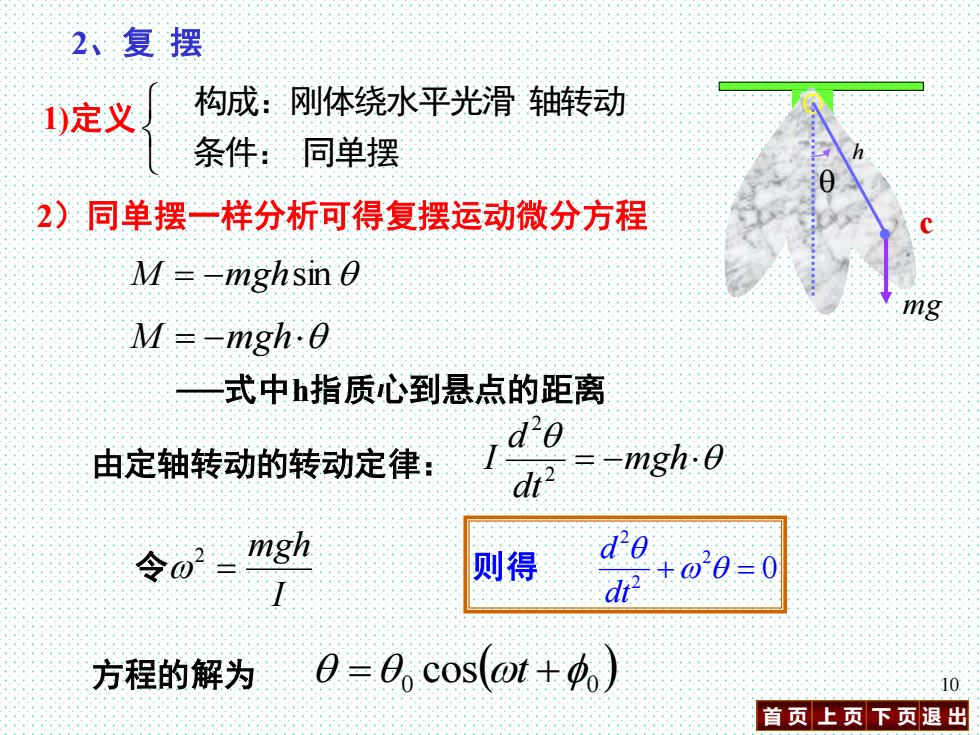
2、复摆 )定义 构成:刚体绕水平光滑轴转动 条件:同单摆 2)同单摆一样分析可得复摆运动微分方程 M=-mghsin 0 M=-mgh-0 式中h指质心到悬点的距离 d20 由定轴转动的转动定律: d -mgh.0 令o2=8h 则得 I d +020=0 方程的解为 e=0 cos(ot+) 10 首页上页下页退出
首 页 上 页 下 页 退 出 10 2)同单摆一样分析可得复摆运动微分方程 2、复 摆 I mgh = 2 令 0 2 2 2 + = dt d 则得 M = −mghsin M = −mgh ──式中h指质心到悬点的距离 = −mgh dt d I 2 2 由定轴转动的转动定律: 方程的解为 ( ) 0 0 = cos t + ⊙⊙ ● c h mg 1)定义 条件: 同单摆 构成:刚体绕水平光滑 轴转动