
山东程上太军程 提纲 SHANDONG UNIVERSITY OF TECHNOLOOY 华会会学3会华深会 一、递归的概念 二、分治法的基本思想 三、分治法的应用 2025年4月3日 6
2025年4月3日 6 提纲 一、递归的概念 二、分治法的基本思想 三、分治法的应用

G 归东置子太军 提纲 SHANDONG UNIVERSITY OF TECHNOLOGY 一、 递归的概念 二、分治法的基本思想 三、分治法的应用 2025年4月3日
2025年4月3日 7 提纲 一、递归的概念 二、分治法的基本思想 三、分治法的应用

白本程子太程 递归的概念 SHANDONG UNIVERSITY OF TECINOLOGY 器会清的合实点会3冷华品品条 直接或间接地调用自身的算法称为递归算法。 用函数自身给出定义的函数称为递归函数。 ● 由分治法产生的子问题往往是原问题的较小 模式,这就为使用递归技术提供了方便。在 这种情况下,反复应用分治手段,可以使子 问题与原问题类型一致而其规模却不断缩小, 最终使子问题缩小到很容易直接求出其解。 这自然导致递归过程的产生。 ● 分治与递归像一对孪生兄弟,经常同时应用 在算法设计之中,并由此产生许多高效算法。 下面来看几个实例。 2025年4月3日 8
2025年4月3日 8 递归的概念 ⚫ 直接或间接地调用自身的算法称为递归算法。 用函数自身给出定义的函数称为递归函数。 ⚫ 由分治法产生的子问题往往是原问题的较小 模式,这就为使用递归技术提供了方便。在 这种情况下,反复应用分治手段,可以使子 问题与原问题类型一致而其规模却不断缩小, 最终使子问题缩小到很容易直接求出其解。 这自然导致递归过程的产生。 ⚫ 分治与递归像一对孪生兄弟,经常同时应用 在算法设计之中,并由此产生许多高效算法。 下面来看几个实例
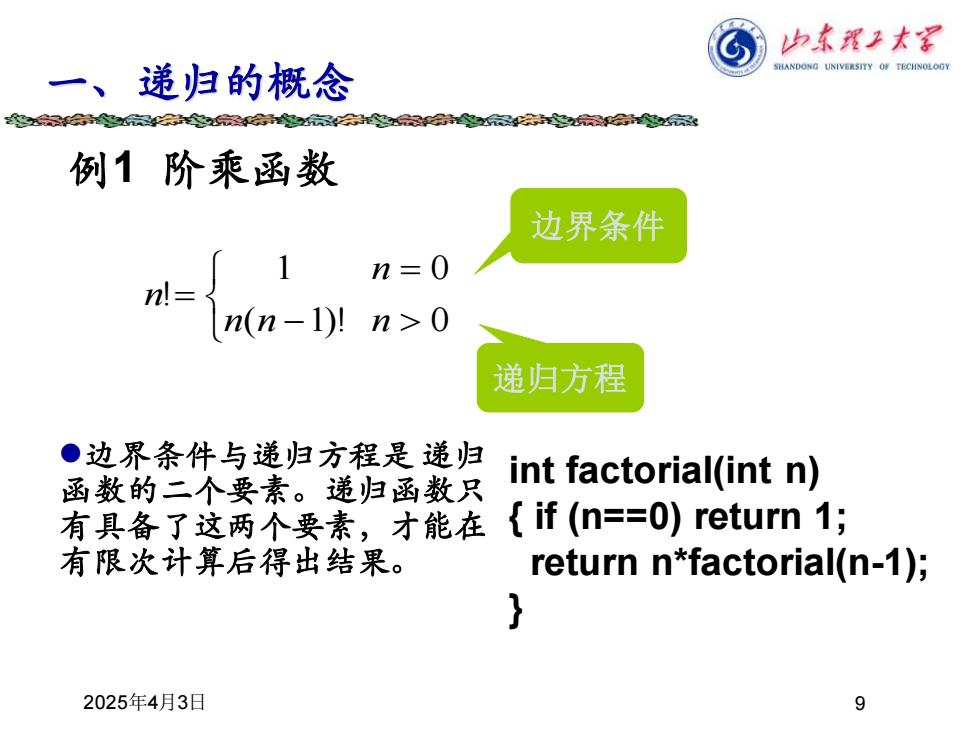
归本程子末军 一、递归的概念 SHANDONG UNIVERSITY OF TECHNOLOGY 例1阶乘函数 边界条件 n= n=0 n(n-1)川 n>0 递归方程 ●边界条件与递归方程是递归 函数的二个要素。递归函数只 int factorial(int n) 有具备了这两个要素,才能在 if (n==0)return 1; 有限次计算后得出结果。 return n*factorial(n-1); 2025年4月3日 9
2025年4月3日 9 一、递归的概念 例1 阶乘函数 0 0 ( 1)! 1 ! = − = n n n n n 边界条件 递归方程 int factorial(int n) { if (n==0) return 1; return n*factorial(n-1); } ⚫边界条件与递归方程是 递归 函数的二个要素。递归函数只 有具备了这两个要素,才能在 有限次计算后得出结果

白东程子太军 一、递归的概念 HANDONG UNIVERSITY OF TECINOLOGY 华会诗3会学S会深公器 ●例2 Fibonacci数列 无穷数列1,1,2,3,5,8,13,21,34,55,.,称为 Fibonaccia数列。递归定义为: 边界条件 1 n=0 F(n)= n=1 F(n-1)+F(n-2)n>=2 递归方程 int fibonacci(int n) if (n <1)return 1; return fibonacci(n-1)+fibonacci(n-2); 2025年4月3日 10
2025年4月3日 10 一、递归的概念 ⚫ 例2 Fibonacci数列 无穷数列1,1,2,3,5,8,13,21,34,55,.,称为 Fibonacci数列。递归定义为: int fibonacci(int n) { if (n <= 1) return 1; return fibonacci(n-1)+fibonacci(n-2); } 边界条件 2 递归方程 1 0 ( 1) ( 2) 1 1 ( ) = = = − + − = n n n F n F n F n