
内容/文件模型 动态文件/内容库 四共计F个文件需要缓存;流行度在各个簇之间不同;且随时间变化. →用c(t)表示t时刻e簇里第流行的文件;其流行度为q(t). ◆用c(t)是最流行的;q(t)≥q(t)≥…≥q(t) ◆ 流行度也表示文件被请求的概率:f=1q(t)=1,e 决策变量:文件缓存/部署在哪里. 四用pr(t)表示t时刻e簇里第k类基站缓存了文件C(t)的概率 四决策变量: [pi1(t) pir(t) PKxF(t)= pki(t) pe(t)】 2020年秋季 16/65 无线互联网
内容/文件模型 2020年秋季 16 / 65 无线互联网 动态文件/内容库 共计F个文件需要缓存; 流行度在各个簇之间不同; 且随时间变化. 用�� � � 表示t时刻e簇里第f流行的文件; 其流行度为�� � � . 用�� � � 是最流行的; �� � � ≥ �� � � ≥ ⋯ ≥ �� � � . 流行度也表示文件被请求的概率: ∑�)� � �� � � = �, ∀� 决策变量: 文件缓存/部署在哪里. 用��� � � 表示t时刻e簇里第k类基站缓存了文件�� � � 的概率. 决策变量: ��×� � � = ��� � � ⋯ ��� � � ⋮ ⋱ ⋮ ��� � � ⋯ ��� � �

Missing Rate (1/2) e簇中一个用户,想要访问文件f,缓存“不中”的概率? ©先看他周围的第k类基站. →通信半径为rk.故只需考虑以他为中心的圆面积πr. →单位面积内有2ke个k类基站处于活动状态. →k类基站部署了文件的概率为P呢r(t). 在他能访问的k类基站中,平均有kep呢r(t)πr?个缓存了文件f. 四由于基站分布是PPP,故有: P[该用户可访问的k类基站中缓存了文件f的基站数目=nk] exp(-kep呢r(t)πr). = akep呢(t)mr)k nk! 令nk=0,得到的就是在k类基站中“不命中”的概率. 四所有K类基站都不命中,才算是本次访问不命中,故有: Pkg-直n-1=en(-么-晚 K K k=1 2020年秋季 17/65 无线互联网
Missing Rate (1/2) 2020年秋季 17 / 65 无线互联网 先看他周围的第k类基站. è通信半径为��. 故只需考虑以他为中心的圆面积��� �. è单位面积内有���个k类基站处于活动状态. èk类基站部署了文件f的概率为��� � � . e簇中一个用户, 想要访问文件f, 缓存“不中”的概率? 在他能访问的k类基站中, 平均有������ � � ��� �个缓存了文件f. 由于基站分布是PPP, 故有: � 该用户可访问的k类基站中缓存了文件f的基站数目 = �� = ��� −������ � � ��� � C ������ � � ��� � �� ��! 令�� = �, 得到的就是在k类基站中“不命中”的概率. 所有K类基站都不命中, 才算是本次访问不命中, 故有: � missing = K �)� � � missing in K − tier = ��� −P �)� � ������ � � ��� �

Missing Rate(2/2) 给定e簇的一个用户,但不指定文件,问Missing概率? ◆只需引入对文件的请求概率:q(t).[即流行度] 四记这个missing概率为fe(t),有: re-名a国-2nap-言u4 考虑任意一个用户,也不指定文件,问Missing概率? 只需引入用户出现在一个簇中的概率: AueSe Ze=1 AueSe [Se为簇面积] 四称该概率为Missing Rate,记为f(t),有: E - hueSe·fe(t) 本文的优化目标 就是最小化f(t). e=1 ∑E-1 AueSe 2020年秋季 18/65 无线互联网
Missing Rate(2/2) 2020年秋季 18 / 65 无线互联网 给定e簇的一个用户, 但不指定文件, 问Missing概率? 只需引入对文件的请求概率: �� � � . [即流行度] 记这个missing概率为�� � , 有: �� � = P �)� � �� � � �[missing] = P �)� � �� � � ��� −P �)� � ������ � � ��� � 考虑任意一个用户, 也不指定文件, 问Missing概率? 只需引入用户出现在一个簇中的概率: ����� ∑�$� � ����� [��为簇面积] 称该概率为Missing Rate, 记为� � , 有: � � = P �)� � ����� C �� � ∑�)� � ����� 本文的优化目标 就是最小化� �
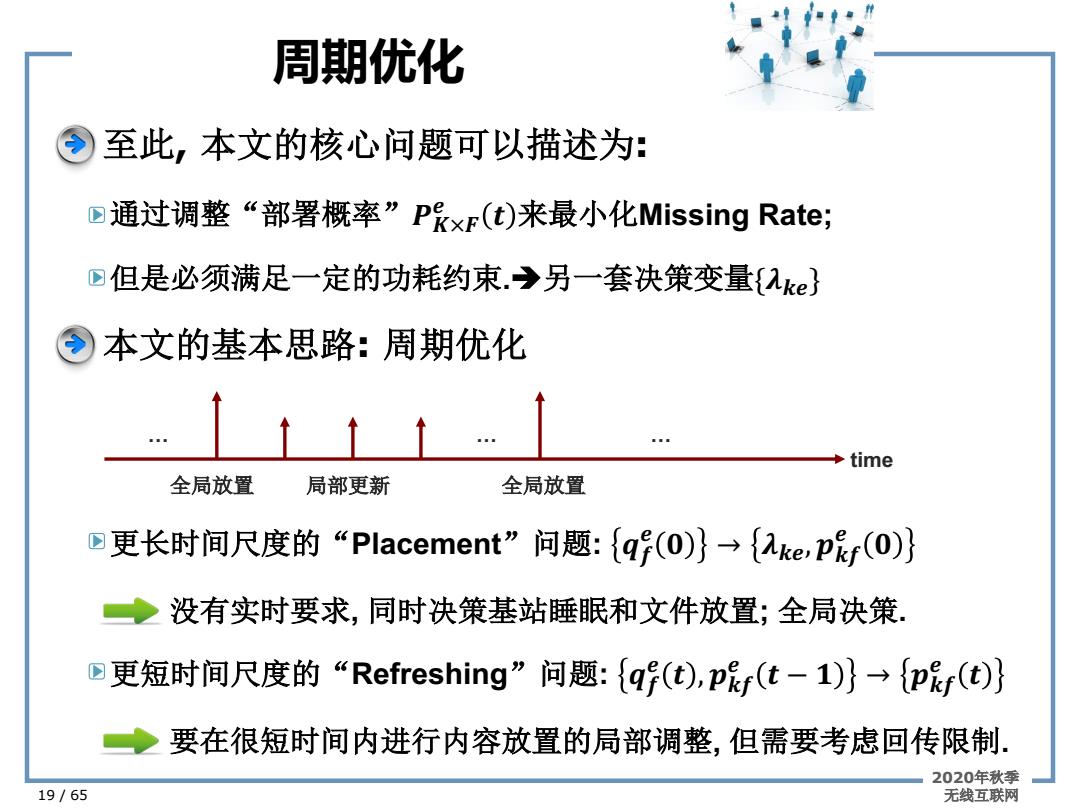
周期优化 至此,本文的核心问题可以描述为: 四通过调整“部署概率”P×p(t)来最小化Missing Rate; 四但是必须满足一定的功耗约束.→另一套决策变量{入ke} 本文的基本思路:周期优化 time 全局放置 局部更新 全局放置 四更长时间尺度的“Placement'”问题:{q(O)}→{2ke,pf(O)} ◆没有实时要求,同时决策基站睡眠和文件放置;全局决策 四更短时间尺度的“Refreshing”问题:{q(t),p呢f(t-1)}→{p呢r(t)} ◆要在很短时间内进行内容放置的局部调整,但需要考虑回传限制. 2020年秋季 19/65 无线互联网
周期优化 2020年秋季 19 / 65 无线互联网 至此, 本文的核心问题可以描述为: 通过调整“部署概率”��×� � � 来最小化Missing Rate; 但是必须满足一定的功耗约束.è另一套决策变量{���} 本文的基本思路: 周期优化 更长时间尺度的“Placement”问题: �� � � → ���, ��� � � 更短时间尺度的“Refreshing”问题: �� � � , ��� � � − � → ��� � � 没有实时要求, 同时决策基站睡眠和文件放置; 全局决策. 要在很短时间内进行内容放置的局部调整, 但需要考虑回传限制. … … time … 全局放置 局部更新 全局放置
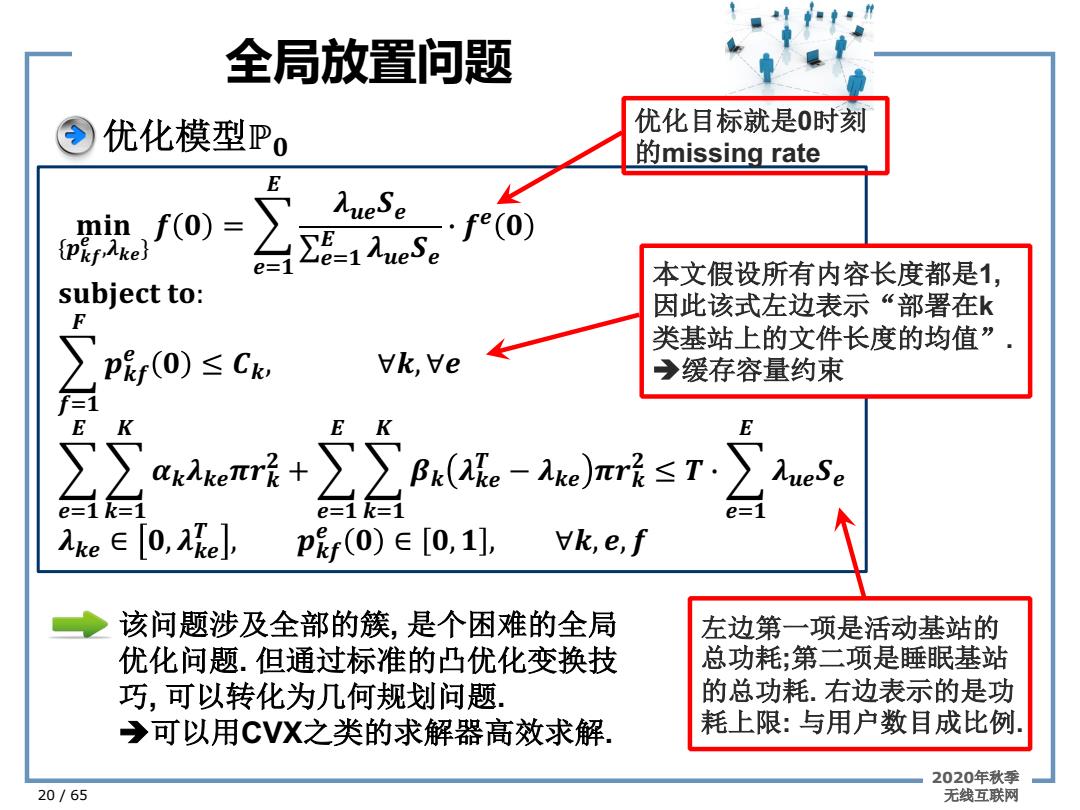
全局放置问题 今优化模型Po 优化目标就是0时刻 的missing rate min、f(0)= pkfAke} e=1 本文假设所有内容长度都是1, subject to: 因此该式左边表示“部署在k ∑p呢ro)≤Cu 类基站上的文件长度的均值” Vk,Ve 缓存容量约束 f=1 E ∑∑aaer喉+∑Bt(a。-aeJm㎡f≤T.∑1es。 e=1k=1 e=1k=1 e=1 ke∈[0,Re] p呢f(0)∈[0,1], Vk,e,f 该问题涉及全部的簇,是个困难的全局 左边第一项是活动基站的 优化问题.但通过标准的凸优化变换技 总功耗;第二项是睡眠基站 巧,可以转化为几何规划问题. 的总功耗.右边表示的是功 →可以用CVX之类的求解器高效求解 耗上限:与用户数目成比例. 2020年秋季 20/65 无线互联网
全局放置问题 2020年秋季 20 / 65 无线互联网 优化模型ℙ� ��� {��� � ,���} � � = P �)� � ����� ∑�)� � ����� C �� � ������� ��: P �)� � ��� � � ≤ ��, ∀�, ∀� P �)� � P �)� � �������� � + P �)� � P �)� � �� ��� � − ��� ��� � ≤ � C P �)� � ����� ��� ∈ �, ��� � , ��� � � ∈ �, � , ∀�, �, � 优化目标就是0时刻 的missing rate 本文假设所有内容长度都是1, 因此该式左边表示“部署在k 类基站上的文件长度的均值”. è缓存容量约束 左边第一项是活动基站的 总功耗;第二项是睡眠基站 的总功耗. 右边表示的是功 耗上限: 与用户数目成比例. 该问题涉及全部的簇, 是个困难的全局 优化问题. 但通过标准的凸优化变换技 巧, 可以转化为几何规划问题. è可以用CVX之类的求解器高效求解