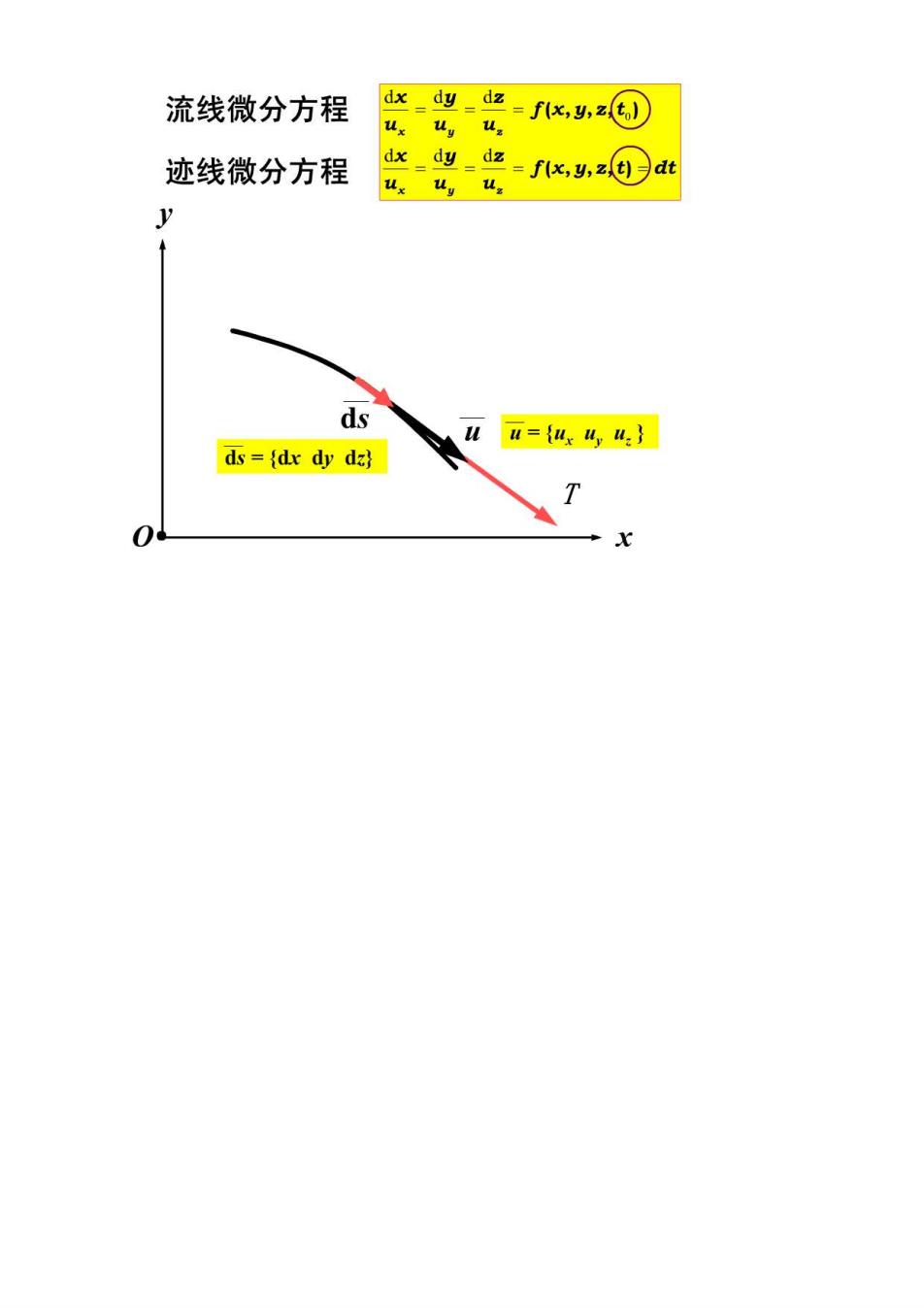
流线微分方程 x_y-业=fx,yz0》 ux uy u 迹线微分方程 dxdydz =fx,y de ux uy u, y ds uu={4,4:} ds=dx dy da T

举例 已知直角坐标系中的速度场4,=x+t:,=y+t:4,=0,试求 t=0时过M(-1,-1)点的流线。 解:由流线的微分方程: d x d y dx_dy dz x +t -y+t ux uy u. 具积分 4,=x+t;4,=-y+t;2=0 (x+0Oy-)=C t=0时过M(-1,-1):C=1 t=0时过M(-1,-1)点的流线:y=1

举例 已知直角坐标系中的速度场4=x+t:4,=y+t:4,=0,试求 t=0时过M(-1,-1)点的迹线。 dx =x+t 解:由迹线的微分方程: dt dx_dy=d==dI =-y+t ux uy u: dt 几求解 4=x+t;4=-y+t;42=0 x=C,e'-t-1 y=C2e'+t-1 t=0时过M(-1,-1):C1=C2=0 y=1消去,得迹线方程:x+y=-2 「x=-t-1

y 迹线 0 M-l,-1) x 流线 t=0时过M(-1,-1):点的流线和迹线示意图

§12.4液体微团运动的基本形式 由理论力学可知,刚体有平移和旋转两种运动形式,而液体 运动则不同。由于液体微团在流场中各点的速度不同,但又要保 持液体本身的连续性,因此液体微团除有平移和旋转运动外,还 有变形运动。因此,液体运动远比刚体运动复杂得多,而液体运 动与刚体运动的最大区别就在于液体存在变形运动。 设于时刻,在流场中任取一正交六面体的液体微团。选取六 面体一个角点A(K、y、Z)为基点,设t瞬时A点的速度为uA,uA 在x、y、z三个坐标轴上的分量分别为u,,u2。其它各点的 速度都与A点不同,其变化可根据该点位置增量用泰勒级数表示 。现另取微团中距A点ds处的p点分析,设该点坐标为p(x+dx、 y+dy、z+dz),则该点在各坐标轴上的速度分量按泰勒级数展开为