例:简支梁受力如图所示.求梁的转角方程和挠度方 程,并确定最大转角0和最大挠度w。 解:1.弯矩方程 M(x)=-P(-x) 2.微分方程和积分 积分法举例2 dw dx2 P-) 图7-6 x)= P(l-x+C 3.支座边界条件定常数 2 w(0)=0,D= PI 6EI w(x)= P-(l-x)+Cx+D 6E1 w(1)=0,C P12 6EI
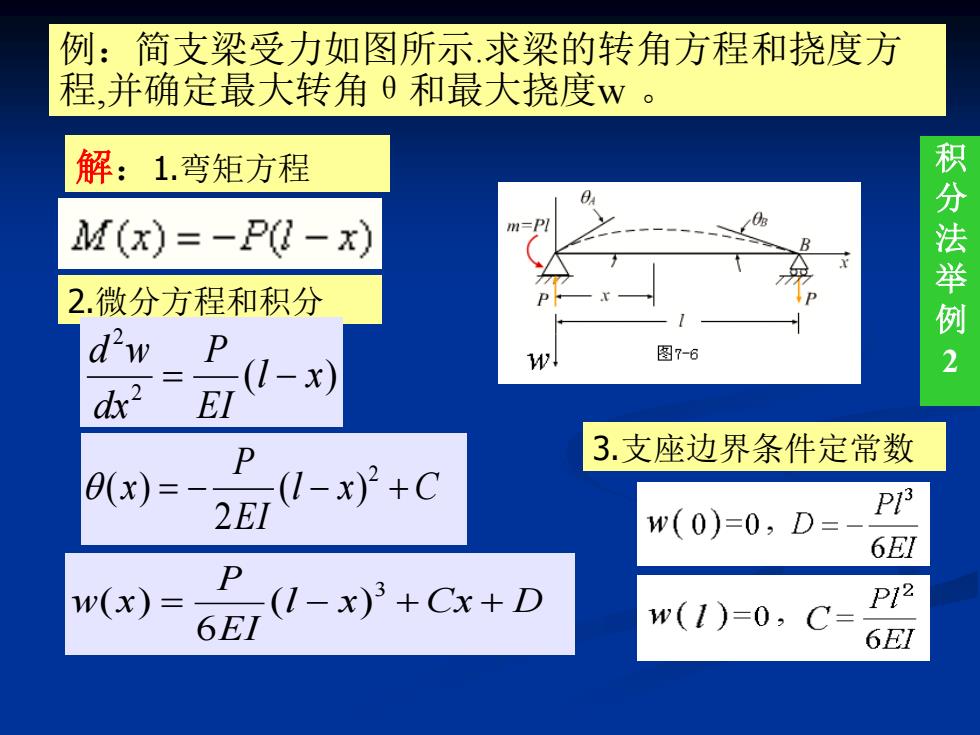
例:简支梁受力如图所示.求梁的转角方程和挠度方 程,并确定最大转角θ和最大挠度w 。 积 分 法 举 例 2 解:1.弯矩方程 2.微分方程和积分 3.支座边界条件定常数 ( ) 2 2 l x EI P dx d w = − l x C EI P x = − − + 2 ( ) 2 ( ) l x Cx D EI P w x = − + + 3 ( ) 6 ( )

得到梁的转角方程和挠度方程分别为 P (1-x)2+ P12 8(x)= 2BI 6E1 w(x)= 1-x+ P 6EI 6E1 6E1 P12 84=8(0)=- 3E1 积分法举例2 8g=B()= PP 6E1 故|8lmx= 发生在支座处。 3E1
积分法举例2

求最大挠度,可令 dw (x)=0,由此解得x0=0.4231, dx "=0.0642 P23 El m12 =0.0625 P13 积分法举例2 2 16EI EI 结论:可用梁中点的挠度近似代 替梁的最大挠度
积 分 法 举 例 2 结论:可用梁中点的挠度近似代 替梁的最大挠度

§13-2奇异函数及其在 确定梁位移中的应用
§13-2 奇异函数及其在 确定梁位移中的应用

Chapter 7 The displacement analysis of elastic rods The application of singular function 定义奇异函数 (x<a)
− = n x a n (x − a) 0 (x a) (x a) ➢ 定义奇异函数 The application of singular function Chapter 7 The displacement analysis of elastic rods