
9.2.1百元百鸡 算法分析: 我们假设公鸡、母鸡、小鸡的只数分别为x、y、Z。我们以三 种鸡总数(+y+z)和买鸡的总钱数(5*x+3*y+z/3)都等于100 为判定条件,穷举出各种鸡的只数
9.2.1 百元百鸡 算法分析: 我们假设公鸡、母鸡、小鸡的只数分别为x、y、z。我们以三 种鸡总数(x+y+z)和买鸡的总钱数(5*x+3*y+z/3)都等于100 为判定条件,穷举出各种鸡的只数

算法9.5: 9.2.1百元百鸡 公鸡数x=1to20 /公鸡数从1枚举到20 算法9.4: 母鸡数y=1to33/母鸡数从1枚举到33 公鸡数x=1t0100 小鸡数z=100-x-y 母鸡数y=1to100 如果(5*x+3*y+z/3)=100那么 小鸡数z=1t0100 /小鸡数从1端到109z的值 如果(x+y+z)=100并且(5*x+3*y+z/3)=100那么 输出x、y、z的值
9.2.1 百元百鸡 算法9.4: 公鸡数 x=1 to 100 //公鸡数从1枚举到100 母鸡数 y=1 to 100 //母鸡数从1枚举到100 小鸡数 z=1 to 100 //小鸡数从1枚举到100 如果(x+y+z)=100 并且 (5*x+3*y+z/3)=100 那么 输出x、y、z的值 算法9.5: 公鸡数x=1 to 20 //公鸡数从1枚举到20 母鸡数y=1 to 33 //母鸡数从1枚举到33 小鸡数 z=100-x-y 如果 (5*x+3*y+z/3)=100 那么 输出x、y、z的值
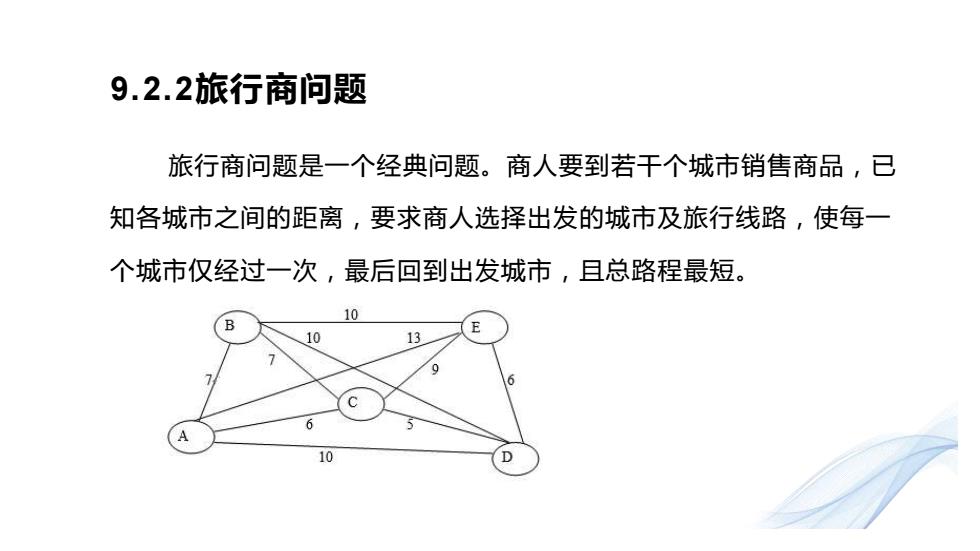
9.2.2旅行商问题 旅行商问题是一个经典问题。商人要到若干个城市销售商品,已 知各城市之间的距离,要求商人选择出发的城市及旅行线路,使每一 个城市仅经过一次,最后回到出发城市,且总路程最短。 10 B 10 13 6 10 D
9.2.2旅行商问题 旅行商问题是一个经典问题。商人要到若干个城市销售商品,已 知各城市之间的距离,要求商人选择出发的城市及旅行线路,使每一 个城市仅经过一次,最后回到出发城市,且总路程最短

10 10 13 9.2.2旅行商问题 10 D 采用穷举法逐一计算出每一条线路的距离,从中找到距离最短的 路线就是问题的解。我们以图9.3所示的5个城市为例来讲解这个算法 ,并要求商人从A城市出发,来求得最短路径。这时只需考虑用A开头 的排列即可,一共有4!种可能
9.2.2旅行商问题 采用穷举法逐一计算出每一条线路的距离,从中找到距离最短的 路线就是问题的解。我们以图9.3所示的5个城市为例来讲解这个算法 ,并要求商人从A城市出发,来求得最短路径。这时只需考虑用A开头 的排列即可,一共有4!种可能
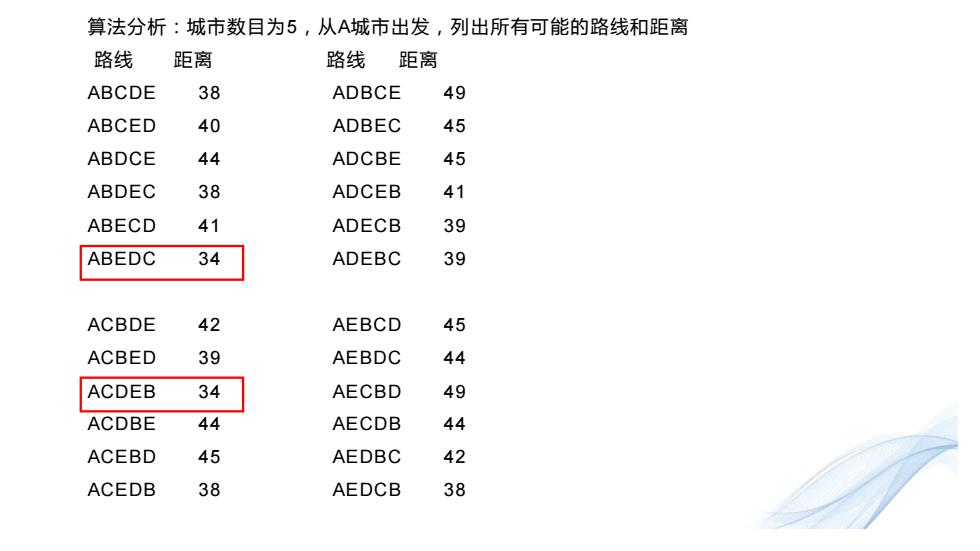
算法分析:城市数目为5,从A城市出发,列出所有可能的路线和距离 路线 距离 路线 距离 ABCDE 38 ADBCE 49 ABCED 40 ADBEC 45 ABDCE 44 ADCBE 45 ABDEC 38 ADCEB 41 ABECD 41 ADECB 39 ABEDC 34 ADEBC 39 ACBDE 42 AEBCD 45 ACBED 39 AEBDC 44 ACDEB 34 AECBD 49 ACDBE 44 AECDB 44 ACEBD 45 AEDBC 42 ACEDB 38 AEDCB 38
算法分析:城市数目为5,从A城市出发,列出所有可能的路线和距离 路线 距离 路线 距离 ABCDE 38 ADBCE 49 ABCED 40 ADBEC 45 ABDCE 44 ADCBE 45 ABDEC 38 ADCEB 41 ABECD 41 ADECB 39 ABEDC 34 ADEBC 39 ACBDE 42 AEBCD 45 ACBED 39 AEBDC 44 ACDEB 34 AECBD 49 ACDBE 44 AECDB 44 ACEBD 45 AEDBC 42 ACEDB 38 AEDCB 38