
8 (E+T )# Reduce:E->E+T 9 why?不用E->T 9 (E )# 若使用了E->T,在栈中形成的(E+E不是规范句 型的活前缀(viable prefixes) (E+E不能和任何产生式的右端匹配(E+E)不是 规范句型 活前缀是规范句型(右句型)的前缀,但不超过 句柄 移进归约分析的栈中出现的内容加上余留输入 构成规范句型
8 (E + T )# Reduce:E –> E + T 9 why?不用 E –> T 9 (E ) # 若使用了E –> T,在栈中形成的(E+E不是规范句 型的活前缀(viable prefixes) (E+E不能和任何产生式的右端匹配 (E+E)不是 规范句型 活前缀 是规范句型(右句型)的前缀,但不超过 句柄 ❖ 移进归约分析的栈中出现的内容加上余留输入 构成规范句型

规范推导规范句型规范归约 最右推导:在推导的任何一步a→B,其中a、B是句型,都是对α中 的最右非终结符进行替换 最右推导被称为规范推导。 由规范推导所得的句型称为规范句型 GS:S→EE→E+rlTT→(E)|int S→E→T→(E)→(E+T)→(E+int) →(T+int)→(int+int) 规范归约 假定a是G的一个句子,称序列an,an1,a是a的一个规范归约 如果该序列满足: (1)an= a (2)a。为文法的开始符号 (3)对任何j,0心j=n,aj-1是从a经把句柄替换为相应产生式的左部 而得到的
规范推导 规范句型 规范归约 最右推导:在推导的任何一步αβ,其中α、β是句型,都是对α中 的最右非终结符进行替换 最右推导被称为规范推导。 由规范推导所得的句型称为规范句型 G[S]: S→E E→E+T|T T→(E)|int SE T (E) (E+T) (E+int) (T+int) (int+int) 规范归约 假定α是G的一个句子,称序列αn ,αn-1 …,α0是 α的一个规范归约 如果该序列满足: (1) αn = α (2) α0为文法的开始符号 (3)对任何j,0<j<=n, αj-1是从αj经把句柄替换为相应产生式的左部 而得到的

文法要求 shift-reduce or reduce-reduce (conflicts) 分析程序不能决定是shift还是reduce 或者分析程序归约时有多个产生式可选 例子(dangling else): S->if E then S if E then S else S 如输入if E then if E then S else S 分析某一时刻,栈的内容:if E then if E then S 而else是下一token归约还是移进?
文法要求 shift-reduce or reduce-reduce 冲突(conflicts) 分析程序不能决定是shift 还是 reduce 或者分析程序归约时有多个产生式可选 例子 ( dangling else) : S –> if E then S | if E then S else S 如输入if E then if E then S else S 分析某一时刻,栈的内容:if E then if E then S 而 else 是下一 token 归约还是移进?

特定的一种shif-reduce实现技术 LR分析 L R最右推导 分析器模型和分析算法 工R分析特征讨论
特定的一种shift-reduce实现技术 LR分析 L R 最右推导 分析器模型和分析算法 LR 分析特征讨论
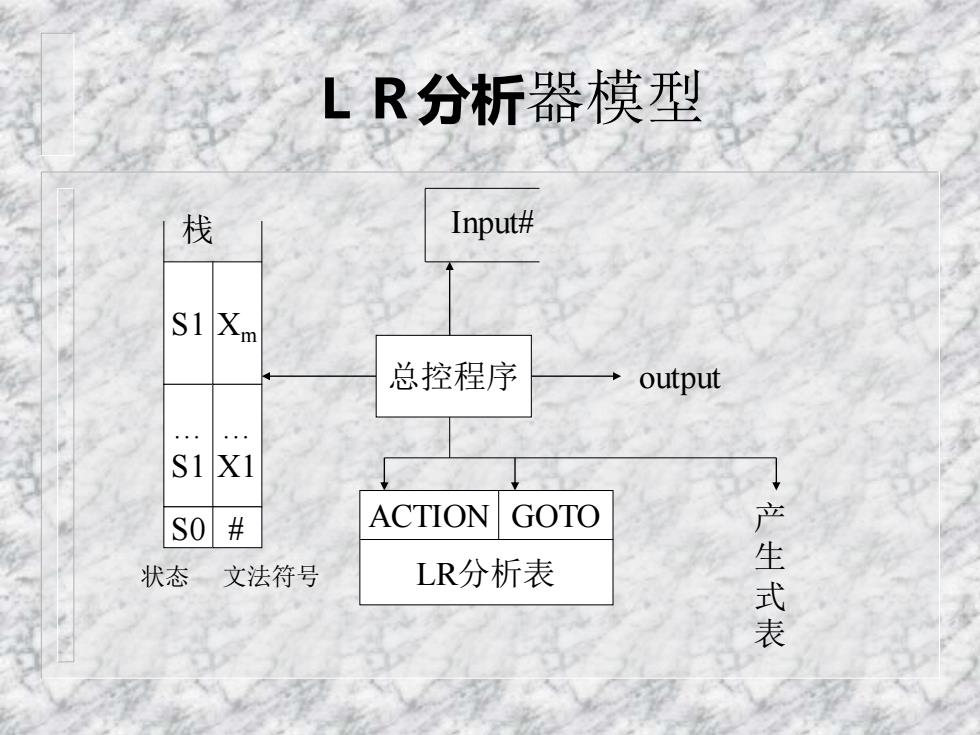
LR分析器模型 栈 Input# S1Xm 总控程序 output S1X1 S0# ACTION GOTO 状态文法符号 LR分析表 产生式表
LR分析器模型 总控程序 output Input# S1 Xm … S1 … X1 S0 # 栈 状态 文法符号 ACTION GOTO LR分析表 产 生 式 表