
2.2.1 Dijkstra集中式算法 ●第一种类型的算法以集中式的风格进行路由 。Dijkstra集中式算法可以发现一个源节点到所 有其他节点的最短路径。 ●Dijkstra集中式算法需求: 需要了解给定网络的全局拓扑消息,即: 网络中所有其它节点的列表; 节点之间的所有链接; 每个链接的代价
2.2.1 Dijkstra集中式算法 ⚫ 第一种类型的算法以集中式的风格进行路由 ⚫ Dijkstra集中式算法可以发现一个源节点到所 有其他节点的最短路径。 ⚫ Dijkstra集中式算法需求: ⚫ 需要了解给定网络的全局拓扑消息,即: 网络中所有其它节点的列表; 节点之间的所有链接; 每个链接的代价

2.2.1 Dijkstra集中式算法: 算法描述 设 D(W)是从源s到节点V的距离(沿给定路径的链接的代价的 和) (V,W是节点v和w之间的代价 Dijkstra算法如下: 1. 设N={s}; 对不在N中的每一个节点V,令D(V=(s,V)。 对那些没有连接到s的节点赋值为∞。 2. 找到不在N中的一个节点W,使DW最小并将w加入N; 然后对所有不在N中的其它节点计算并更新D(V): D(v):min[D(V),D(w)+l(w,V)] 重复步骤2,直到所有节点都在N中
2.2.1 Dijkstra集中式算法: 算法描述 设 D(v)是从源s到节点v的距离(沿给定路径的链接的代价的 和) l(v,w)是节点v和w之间的代价 Dijkstra算法如下: 1. 设N={s}; 对不在N中的每一个节点v,令D(v)=l(s,v)。 对那些没有连接到s的节点赋值为∞。 2. 找到不在N中的一个节点w,使D(w)最小并将w加入N; 然后对所有不在N中的其它节点计算并更新D(v): D(v) := min[D(v), D(w)+l(w,v)] 重复步骤2,直到所有节点都在N中
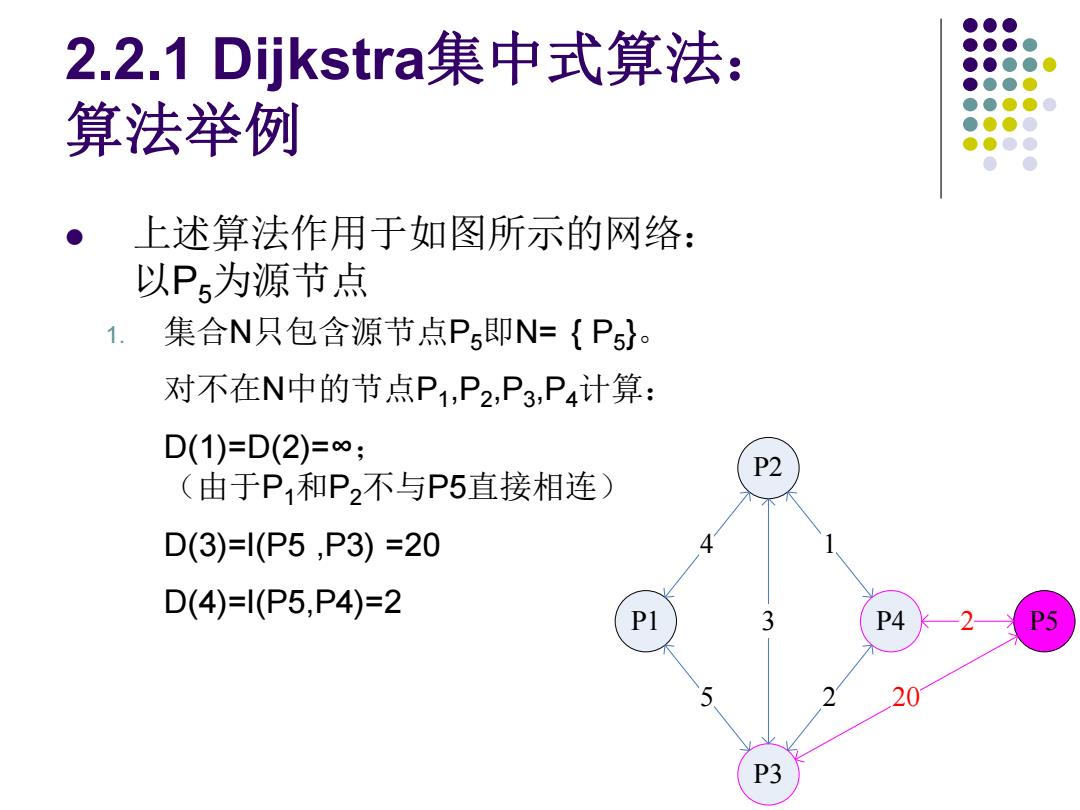
2.2.1 Dijkstra集中式算法: 算法举例 上述算法作用于如图所示的网络: 以P5为源节点 1. 集合N只包含源节点P5即N={Ps}。 对不在N中的节点P1,P2,P3,P4计算: D(1)=D(2)=∞; (由于P1和P2不与P5直接相连) P2 D(3)=l(P5,P3)=20 D(4)=1(P5,P4)=2 P1 3 P4 -2 2 20 P3
2.2.1 Dijkstra集中式算法: 算法举例 ⚫ 上述算法作用于如图所示的网络: 以P5为源节点 1. 集合N只包含源节点P5即N= { P5 }。 对不在N中的节点P1 ,P2 ,P3 ,P4计算: D(1)=D(2)=∞; (由于P1和P2不与P5直接相连) D(3)=l(P5 ,P3) =20 D(4)=l(P5,P4)=2 P1 P2 P3 P4 P5 4 5 3 1 2 2 20
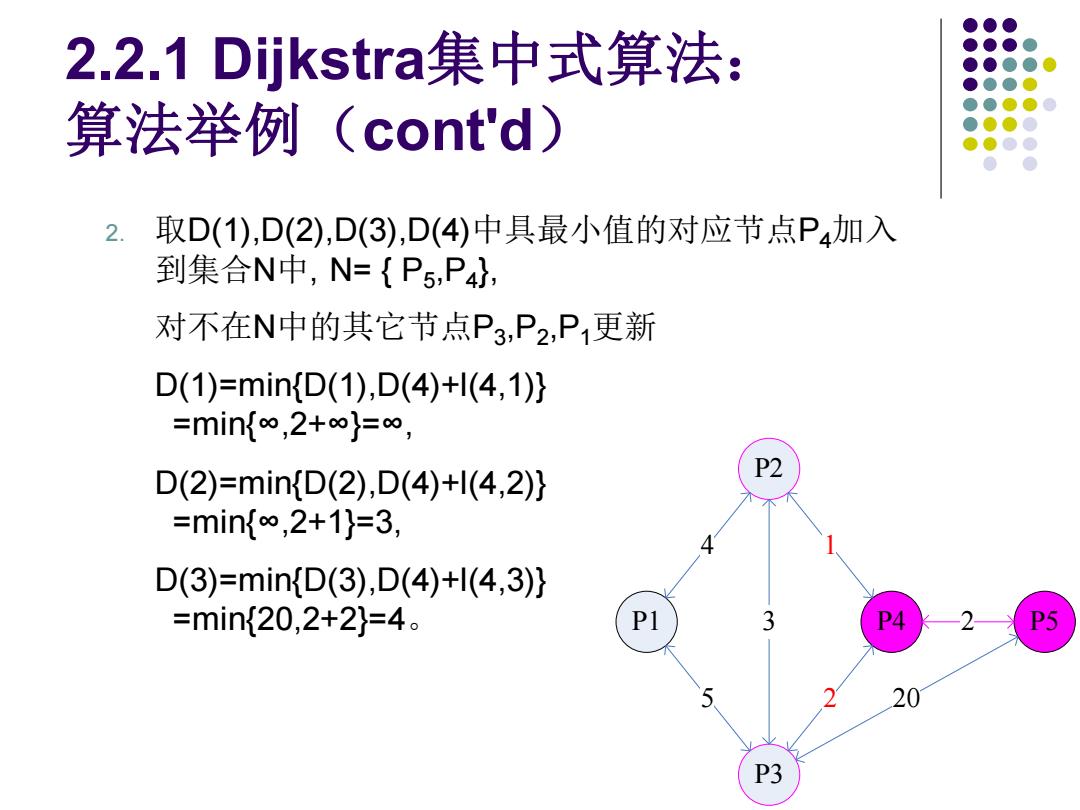
2.2.1 Dijkstra集中式算法: 算法举例(cont'd) 2. 取D(1),D(2),D(3),D(4)中具最小值的对应节点P4加入 到集合N中,N={P5,P4}, 对不在N中的其它节点P3,P2,P1更新 D(1)=min{D(1),D(4)+l(4,1)} =min{∞,2+∞}=∞, D(2)=min{D(2),D(4)+l(4,2)} P2 =min{∞,2+1}=3, D(3)=min{D(3),D(4)+l(4,3)} =min{20,2+2}=4。 P1 3 PS 20 P3
2.2.1 Dijkstra集中式算法: 算法举例(cont'd) 2. 取D(1),D(2),D(3),D(4)中具最小值的对应节点P4加入 到集合N中, N= { P5 ,P4 }, 对不在N中的其它节点P3 ,P2 ,P1更新 D(1)=min{D(1),D(4)+l(4,1)} =min{∞,2+∞}=∞, D(2)=min{D(2),D(4)+l(4,2)} =min{∞,2+1}=3, D(3)=min{D(3),D(4)+l(4,3)} =min{20,2+2}=4。 P1 P2 P3 P4 P5 4 5 3 1 2 2 20
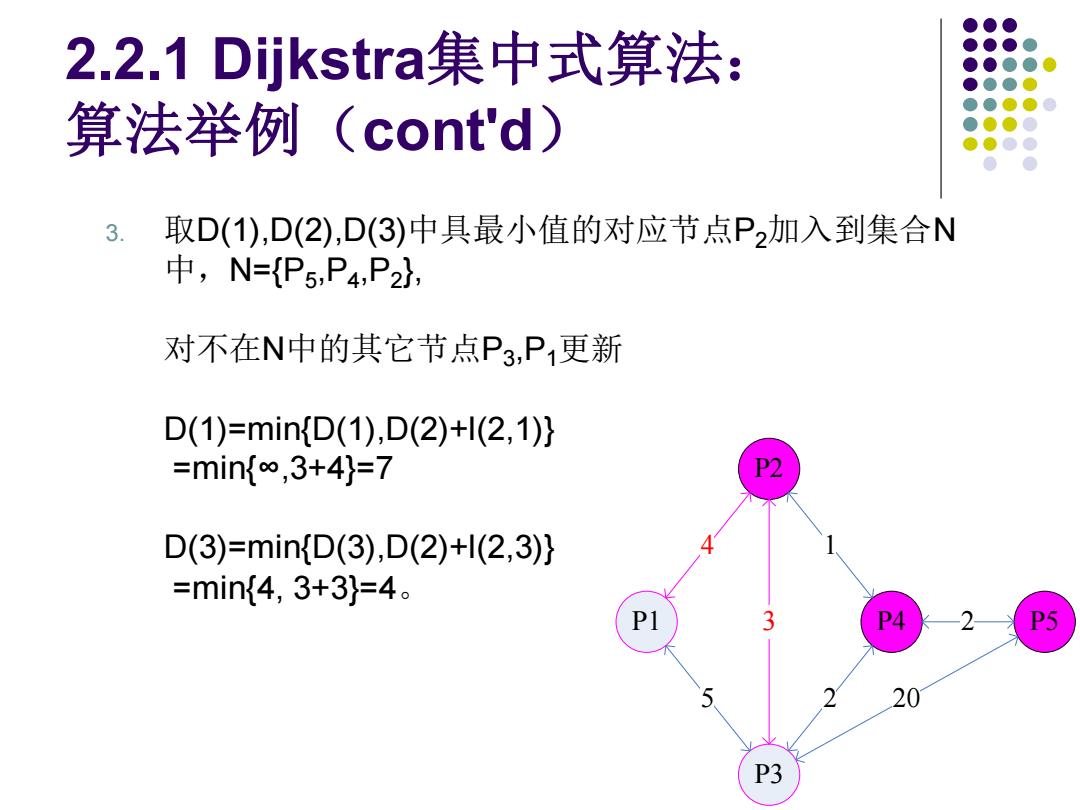
2.2.1 Dijkstra集中式算法: 算法举例(cont'd) 3. 取D(1),D(2),D(3)中具最小值的对应节点P,加入到集合N 中,N={P5,P4,P2}, 对不在N中的其它节点P3,P1更新 D(1)=min{D(1),D(2)+l(2,1)} =min{∞,3+4}=7 P2 D(3)=minD(3),D(2)+l(2,3)} =min{4,3+3}=4。 P1 PS 20 P3
2.2.1 Dijkstra集中式算法: 算法举例(cont'd) 3. 取D(1),D(2),D(3)中具最小值的对应节点P2加入到集合N 中,N={P5 ,P4 ,P2 }, 对不在N中的其它节点P3 ,P1更新 D(1)=min{D(1),D(2)+l(2,1)} =min{∞,3+4}=7 D(3)=min{D(3),D(2)+l(2,3)} =min{4, 3+3}=4。 P1 P2 P3 P4 P5 4 5 3 1 2 2 20