
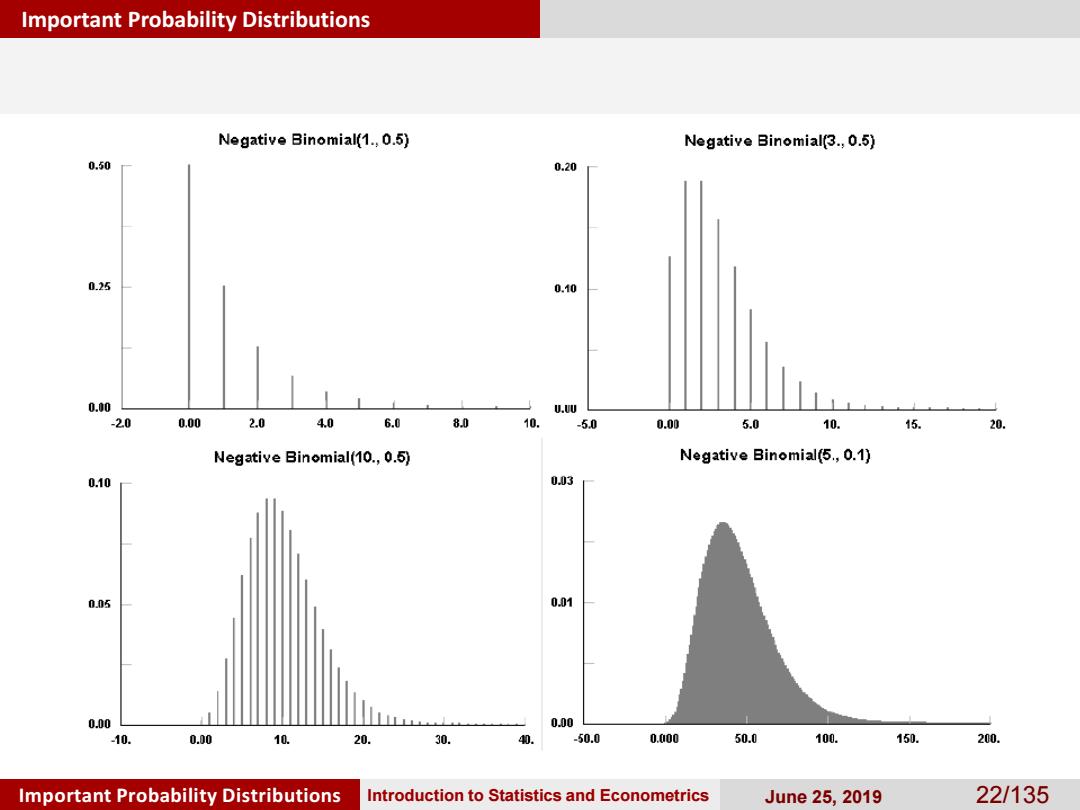
Important Probability Distributions Discrete Probability Distributions Negative Binomial Distribution There are r-1 successes in the first X-1 trials and the X-th trial is a success,so the PMF of X fx(x)= [(g=i)p-11-p)a-10--]p =(-)p(1-p)x-, x=r,T+1,·· To be Continued Important Probability Distributions Introduction to Statistics and Econometrics June25,2019 21/135
Important Probability Distributions Important Probability Distributions Introduction to Statistics and Econometrics June 25, 2019 21/135 Negative Binomial Distribution Discrete Probability Distributions To be Continued
Important Probability Distributions Negative Binomial(1.,0.5) Negative Binomial(3.,0.5) 0.50 0.20 0.25 0.10 0.00 U.UU -20 0.00 2.0 4.0 6.0 8.0 10. -5.0 0.00 5.0 10. 15. 20. Negative Binomial(10.,0.5) Negative Binomial(5.,0.1) 0.10 0.03 0.05 0.01 0.00 0.00 10. 0.00 10. 20. 30. 40. -50.0 0.000 50.0 100. 150. 200. Important Probability Distributions Introduction to Statistics and Econometrics June25,2019 22/135
Important Probability Distributions Important Probability Distributions Introduction to Statistics and Econometrics June 25, 2019 22/135

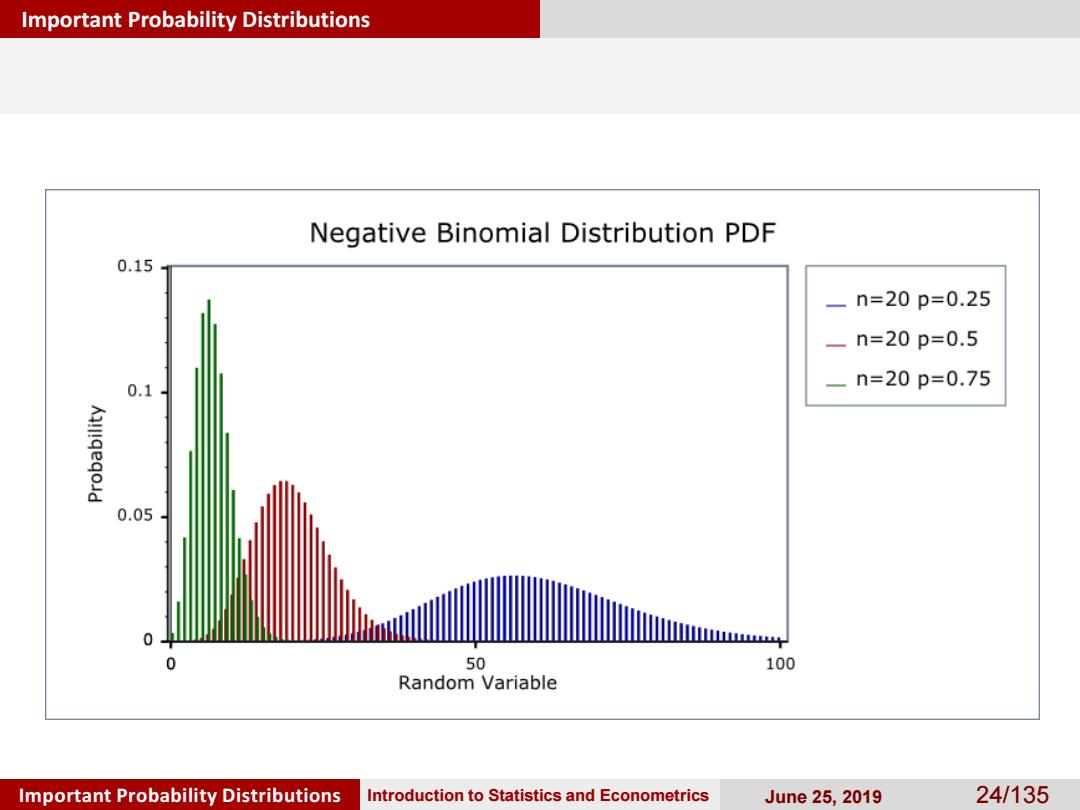
Important Probability Distributions Discrete Probability Distributions Negative Binomial Distribution NB(n,p)is sometimes defined in terms of the number of failures when obtaining the r-th success,Y=X-r. The support of Y is the set of all nonnegative inte- gers{0,1,·}. The PMF of Y fy(y)=P(Y=y) =P(X=y+r) (g+-1)p(1-p),fory=0,1 Important Probability Distributions Introduction to Statistics and Econometrics June25,2019 23/135
Important Probability Distributions Important Probability Distributions Introduction to Statistics and Econometrics June 25, 2019 23/135 Negative Binomial Distribution Discrete Probability Distributions
Important Probability Distributions Negative Binomial Distribution PDF 0.15 n=20p=0.25 _n=20p=0.5 0.1 n=20p=0.75 0.05 50 100 Random Variable Important Probability Distributions Introduction to Statistics and Econometrics June25,2019 24/135
Important Probability Distributions Important Probability Distributions Introduction to Statistics and Econometrics June 25, 2019 24/135

Important Probability Distributions Discrete Probability Distributions Geometric Distribution The geometric distribution is the probability distribution of the number of Bernoulli trials required to obtain the first suc- cess. This is a special case of the negative binomial distribution with Y=1. When r =1,the negative binomial distribution becomes fx(x)=p(1-p)c-1, x=1,2,···. Important Probability Distributions Introduction to Statistics and Econometrics June25,2019 25/135
Important Probability Distributions Important Probability Distributions Introduction to Statistics and Econometrics June 25, 2019 25/135 Geometric Distribution Discrete Probability Distributions