
6.3无损压缩编码 图6.3.2给出了一个实际信源符号的缩减过程。 原始信源 信符缩减步骤 符号 概率 1 2 3 4 5 2 0.4 0.4 0.4 0.4 0.4 >0.6 6 0.2 0.2 0.2 >0.24 >0.36 0.4 0.16 0.16 0.16 0.2 0.24 0.12 0.12 0.12 0.16 0.06 0.06 >0.12 0.04 0.06 5 0.02 图6.3.2霍夫曼编码中的信符缩减过程 Digital Image Processing
Digital Image Processing Digital Image Processing 6.3 无损压缩编码 图6.3.2给出了一个实际信源符号的缩减过程。 给出了一个实际信源符号的缩减过程。 图6.3.2 霍夫曼编码中的信符缩减过程 2 a 6 a 1 a 3 a 7 a 4 a 5 a 0.4 0.2 0.16 0.12 0.06 0.04 0.02 0.06 0.06 0.12 0.16 0.2 0.4 0.16 0.2 0.4 0.12 0.12 0.4 0.24 0.2 0.16 0.4 0.36 0.24 符号 概率 1 2 3 45 原始信源 信符缩减步骤 0.4 0.6
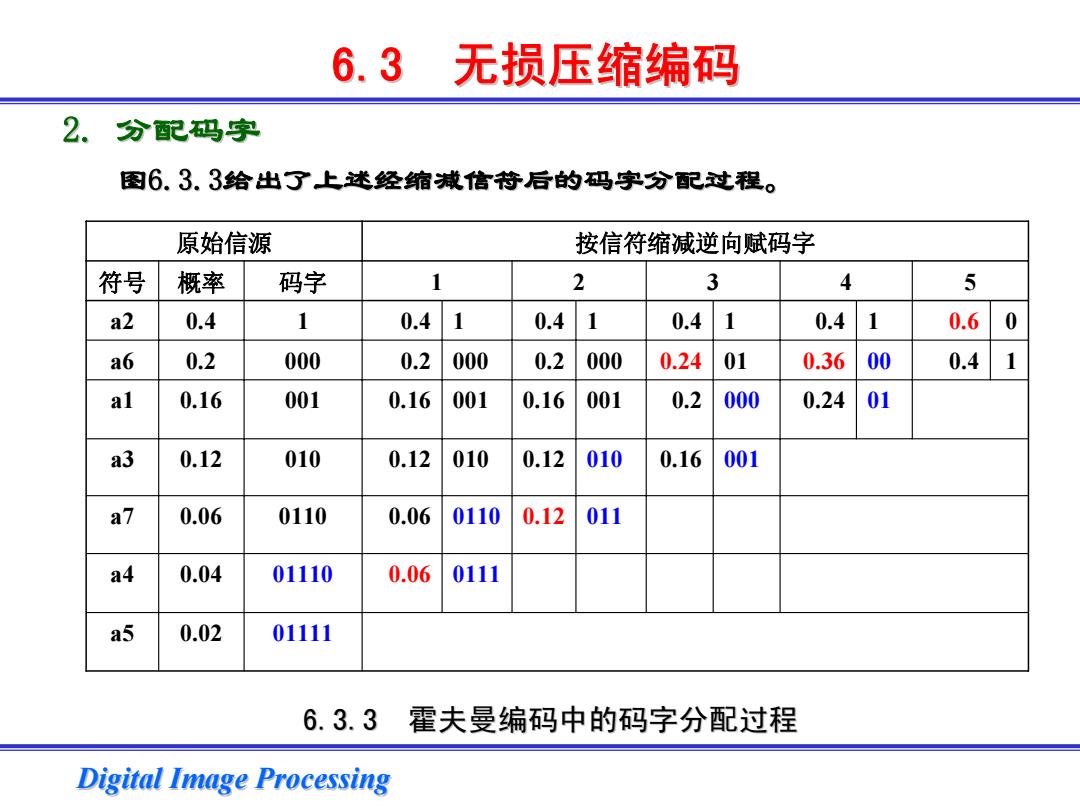
6.3无损压缩编码 2.分配码字 图6.3.3给出了上述经缩减信符后的码字分配过程。 原始信源 按信符缩减逆向赋码字 符号 概率 码字 1 2 3 4 5 a2 0.4 1 0.4 1 0.4 1 0.4 1 0.4 0.6 0 a6 0.2 000 0.2 000 0.2 000 0.24 01 0.36 00 0.4 1 al 0.16 001 0.16 001 0.16 001 0.2 000 0.24 01 a3 0.12 010 0.12 010 0.12 010 0.16 001 a7 0.06 0110 0.06 0110 0.12 011 a4 0.04 01110 0.06 0111 a5 0.02 01111 6.3.3霍夫曼编码中的码字分配过程 Digital Image Processing
Digital Image Processing Digital Image Processing 2. 分配码字 图6.3.3给出了上述经缩减信符后的码字分配过程。 6.3.3 霍夫曼编码中的码字分配过程 6.3 无损压缩编码 原始信源 按信符缩减逆向赋码字 符号 概率 码字 1 2 3 45 a2 0.4 1 0.4 1 0.4 1 0.4 1 0.4 1 0.6 0 a6 0.2 000 0.2 000 0.2 000 0.24 01 0.36 00 0.4 1 a1 0.16 001 0.16 001 0.16 001 0.2 000 0.24 01 a3 0.12 010 0.12 010 0.12 010 0.16 001 a7 0.06 0110 0.06 0110 0.12 011 a4 0.04 01110 0.06 0111 a5 0.02 01111
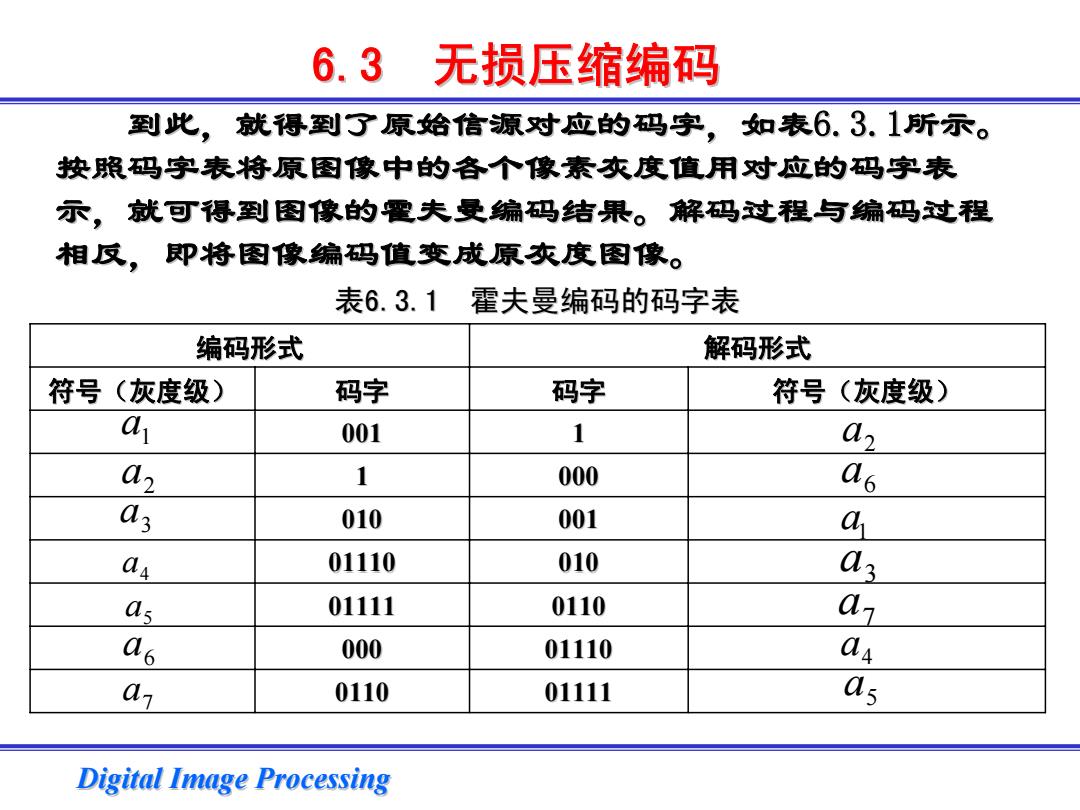
6.3无损压缩编码 到此,就得到了原始信源对应的码字,如表6.3.1所示。 按照码字表将原图像中的各个像素灰度值用对应的码字表 示,就可得到图像的霍夫曼编码结果。解码过程与编码过程 相反,即将图像编码值变成原灰度图像。 表6.3.1霍夫曼编码的码字表 编码形式 解码形式 符号(灰度级) 码字 码字 符号(灰度级) a 001 1 az az 1 000 as a; 010 001 4 a 01110 010 a3 as 01111 0110 az as 000 01110 a az 0110 01111 as Digital Image Processing
Digital Image Processing Digital Image Processing 到此,就得到了原始信源对应的码字,如表 到此,就得到了原始信源对应的码字,如表6.3.1所示。 按照码字表将原图像中的各个像素灰度值用对应的码字表 按照码字表将原图像中的各个像素灰度值用对应的码字表 示,就可得到图像的霍夫曼编码结果。解码过程与编码过程 示,就可得到图像的霍夫曼编码结果。解码过程与编码过程 相反,即将图像编码值变成原灰度图像。 相反,即将图像编码值变成原灰度图像。 表6.3.1 霍夫曼编码的码字表 6.3 无损压缩编码 编码形式 解码形式 符号(灰度级) 码字 码字 符号(灰度级) 001 1 1 000 010 001 01110 010 01111 0110 000 01110 0110 01111 1 a 2 a 2 a a1 3 a 4 a3 a a4 5 a a5 a6 a6 a7 7 a

6.3无损压缩编码 同时也可以计算与编码性能相关的几个参数: (1) 信源的熵 H(0=-2P(a,)log,Pa)=2325 (2) 霍夫曼编码的平均码字长 Lae=∑1(a,)p(a,) i-1 =3×0.16+1×0.4+3×0.12+5×0.04+5×0.02+3×0.2+4×0.06 =2.380 (3) 霍夫曼编码的效率 H(A2.325 n= 0.977 2.380 Digital Image Processing
Digital Image Processing Digital Image Processing 6.3 无损压缩编码 同时也可以计算与编码性能相关的几个参数 同时也可以计算与编码性能相关的几个参数: (1) 信源的熵 (2) 霍夫曼编码的平均码字长 霍夫曼编码的平均码字长 (3) 霍夫曼编码的效率 霍夫曼编码的效率 7 2 1 ( ) ( )log ( ) 2.325 i i i H A Pa Pa = = −∑ = 7 1 ( )( ) 3 0.16 1 0.4 3 0.12 5 0.04 5 0.02 3 0.2 4 0.06 2.380 avg i i i L la pa = = = × +× +× +× +× +× + × = ∑ ( ) 2.325 0.977 2.380 avg H A L η ===

6.3无损压缩编码 (4) 元余度 R=(1-7)×100%=2.3% (5)压缩比 m 3 =1.26 2.380 霍夫曼编码是无失真编码中效率较高的一种编码方法。在 分配码字过程中,随机赋“0”和“1”的不同,结果会使码字不同 (不唯一),而码字长和平均码字长不会改变,它也是唯一可 解码的。但其缺点是信源缩减过程复杂,运算量大。为克服这 个缺点,人们也相继提出了一些改进方法。 Digital Image Processing
Digital Image Processing Digital Image Processing 6.3 无损压缩编码 (4) 冗余度 (5) 压缩比 霍夫曼编码是无失真编码中效率较高的一种编码方法。在 霍夫曼编码是无失真编码中效率较高的一种编码方法。在 分配码字过程中,随机赋 分配码字过程中,随机赋“0”和“1”的不同,结果会使码字不同 的不同,结果会使码字不同 (不唯一),而码字长和平均码字长不会改变,它也是唯一可 (不唯一),而码字长和平均码字长不会改变,它也是唯一可 解码的。但其缺点是信源缩减过程复杂,运算量大。为克服这 解码的。但其缺点是信源缩减过程复杂,运算量大。为克服这 个缺点,人们也相继提出了一些改进方法。 个缺点,人们也相继提出了一些改进方法。 = −η × = %3.2%100)1( RD 3 1.26 2.380 R avg m C L == =