
2.2符号和符号串 前缀 移走符号串尾部的零个或多于 对于每个符号 如:e,a,ab,abc是符号串a 串S,S和e两 后缀 者都是符号串S 的前缀,后缀 ·删去符号串头部的零个和子串。 的符号 串。如8,c,bc,凸c是f号串aoc时 子串 ·从$中删去一个前缀和一个后缀得到的符号串。 如:bc是符号串abc的一个子串 真前缀,真后缀,真子串 ·任何非空符号串X,相应地,是$的前缀,后缀或子 串,并且S≠x 一编译原理一 36 返回
2.2 符号和符号串 • 移走符号串尾部的零个或多于零个符号得到的符号串. 如: ε, a, ab, abc是符号串abc的前缀. 前缀 •删去符号串头部的零个或多于零个符号得到的符号 串。如:ε, c, bc, abc是符号串abc的后缀 后缀 •从s中删去一个前缀和一个后缀得到的符号串。 如:bc是符号串abc的一个子串 子串 对于每个符号 串s, s和ε两 者都是符号串s 的前缀,后缀 和子串。 •任何非空符号串x,相应地,是s的前缀,后缀或子 串,并且s x 真前缀,真后缀,真子串 -编译原理- 36
2.2 符号和符号串 符号串的运算 符号串集合的运算 长度 乘积 特号串中符号的个数 AB={ylx∈A且y∈B} ·符号串s的长度记为|s|。8的长度为0 ·若集合A={a,b}B={0,1} ·则AB={a0,a1,b0,b1} ·因为Ex=XE=X,所以{CA={CA=A 有符号串集合A,定义 连接 特号串x、y的连接,是把y的特号写在 A0={8},A1=A,A2=AAA3=AA,. x的符号之后得到的符号串y 方幂 .A=A-1A=AA-1,n>0 ·如x=ab,y=12则xy=ab12 例:A={a,b},Ao={8},A1={a,b},A2= ·注意:一般XyyX,而以=XE {aa,ab,ba,bb}即特号串A的n次方乘积 A+=A1UA2UA3U.UA0 U.称为集合A的正闭包。 方幂 符号串自身连接n次得到的符号串 A*=A0 UAI U A2 UA3 U.UA 闭包 U.称为集合A的闭包。 "an定义为aa.aan个aal=a,a2=aa ·特殊的,a=e ·A+=A*A=AA* A*=AO UA+ 返回 一编译原理一一 37
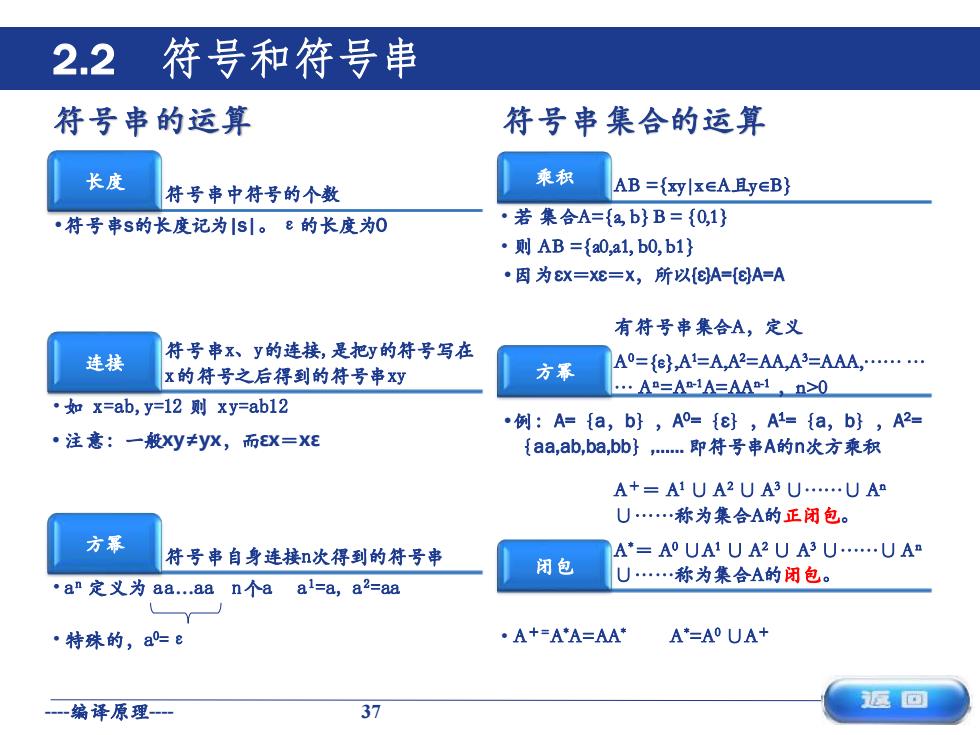
符号串的运算 符号串中符号的个数 长度 •符号串s的长度记为|s|。ε的长度为0 符号串x、y的连接,是把y的符号写在 x的符号之后得到的符号串xy 连接 •如 x=ab,y=12 则 xy=ab12 • 注意:一般xy≠yx,而εx=xε 符号串自身连接n次得到的符号串 方幂 • a n 定义为 aa.aa n个a a1=a, a2=aa •特殊的,a 0=ε 符号串集合的运算 乘积 AB =xy|xA且yB • 若 集合A=a, b B = 0,1 • 则 AB =a0,a1, b0, b1 •因为εx=xε=x,所以{ε}A={ε}A=A 有符号串集合A,定义 A0={ε},A1=A,A2=AA,A3=AAA,. . . An=An-1A=AAn-1 ,n>0 方幂 •例:A={a,b},A 0={ε},A 1={a,b},A 2= {aa,ab,ba,bb},. 即符号串A的n次方乘积 A+= A1 ∪ A2 ∪ A3 ∪.∪ An ∪.称为集合A的正闭包。 A*= A0 ∪A1 ∪ A2 ∪ A3 ∪.∪ An 闭包 ∪.称为集合A的闭包。 • A+=A*A=AA* A*=A0 ∪A+ 2.2 符号和符号串 -编译原理- 37

2.2符号和符号串 例如:L={A~Z,a~zD={0~9] 1.LUD={A~Z,a~z,0~9} 2.LD是由所有用一个字母后跟一个数字 组成的符号串所构成的集合。 3.L4是由所有的四个字母的符号串构 练 的集合。 4.L(LUD)*是由所有的字母打头的字母 和数字组成的符号串所构成的集合 习 5,D是由所有的长度大于等于1的数字串 所构成的集合 一编译原理一 38 返回
练 习 例如:L={A~Z,a~z} D={0~9} 1.L∪D={A~Z,a~z ,0~9} 2.LD是由所有用一个字母后跟一个数字 组成的符号串所构成的集合。 3.L 4是由所有的四个字母的符号串构 的集合。 4.L(L∪D)* 是由所有的字母打头的字母 和数字组成的符号串所构成的集合. 5.D +是由所有的长度大于等于1的数字串 所构成的集合. 2.2 符号和符号串 -编译原理- 38

2.2 符号和俯号串 若A为某语言的基本字符集 A={ab,z,0,1,.9,+,-,X,() ),=.} B为单词集 思考: B={begin,end,if,then,else,for,<标识 符>,<常量>,. 则BcA*。 串、符号 集 语言的句子是定义在B上的符号串。 算感兴趣? 若令C为句子集合,则CcB*,程序cC 返回 一编译原理一一 39
思考: 为什么对符号、 符号串、符号串 集合以及它们的 运算感兴趣? 若A为某语言的基本字符集 A={a,b,.z,0,1,.,9, +,-,×,_/, ( , ), =.} B为单词集 B ={begin, end, if, then,else,for,.,<标识 符>,<常量>,.} 则B A* 。 语言的句子是定义在B上的符号串。 若令C为句子集合,则C B * , 程序 C 2.2 符号和符号串 39 -编译原理-

2.3文法和语言的形式定义 2.3.1文法的定义 V=Vn UVt 称为文法的字汇表 定义1.文法G=(Vn,Vt,P,S) Vn:非终结特号集 规则:U=x Vt:终结符号集 U∈Vn,x∈V* P:产生式或规则的集合 S:开始特号(识别特号)S∈Vn 补充:规则的定义 我们通过建立一组规则,来描述句子的语法结构。 规则是一个有序对(U,x),通常写为:U:=X或U→x|U川=1☒≥0 “=”表示“由.组成” 一编译原理一 40 返回
2.3.1文法的定义 定义1. 文法G=(Vn,Vt,P,S) Vn:非终结符号集 Vt:终结符号集 P:产生式或规则的集合 S:开始符号(识别符号) S∈Vn V=Vn∪Vt 称为文法的字汇表 规则:U ::= x U ∈Vn, x∈V * 补充: 规则的定义 我们通过建立一组规则,来描述句子的语法结构。 规则是一个有序对(U, x), 通常写为: U ::= x 或U → x | U| = 1 |x| 0 “::=”表示“由.组成” 2.3 文法和语言的形式定义 -编译原理- 40