电子科技大学：《机器学习 Machine Learning》课程教学资源（课件讲稿）第5讲 人工神经网络分类器 Classifiers with ANN

7.2.1基本概念-生物神经元 1.生物神经元的结构 细胞体、树突、轴突和突触。 来自其它神经元轴突的神经末梢 树突 轴突 突触 细胞体 细胞核 神经末梢

1．生物神经元的结构 细胞体、树突、轴突和突触。 7.2.1 基本概念 – 生物神经元

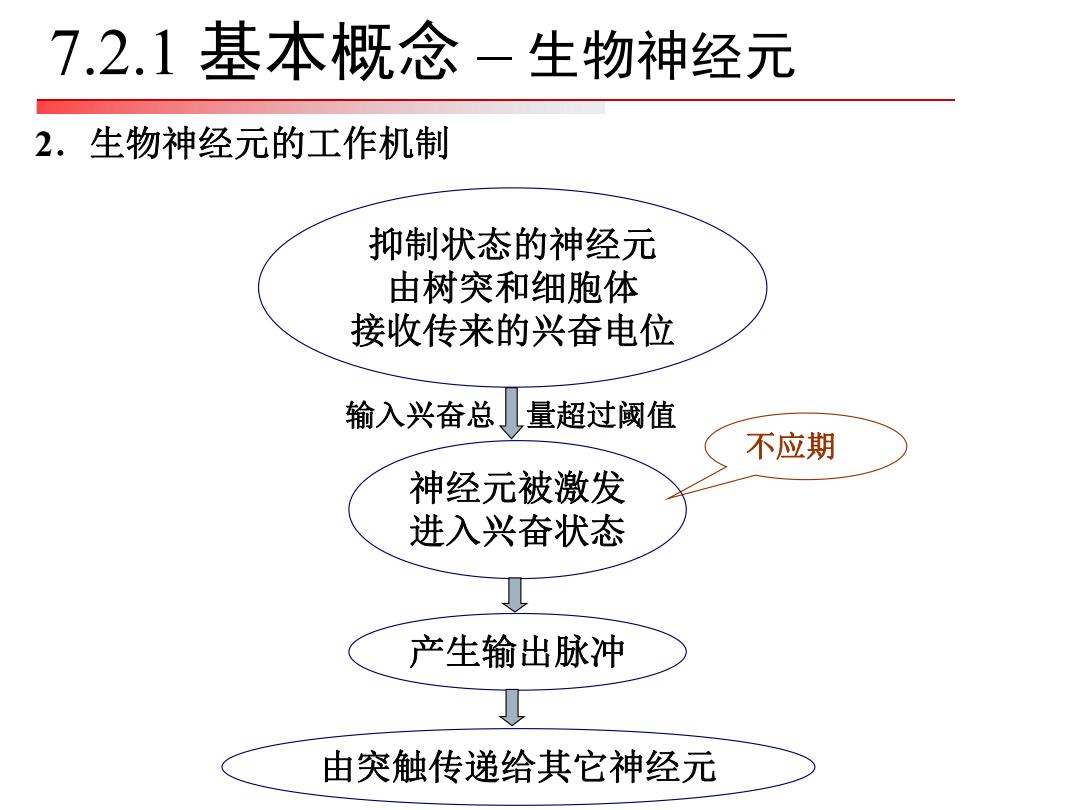
7.2.1基本概念-生物神经元 2.生物神经元的工作机制 抑制状态的神经元 由树突和细胞体 接收传来的兴奋电位 输入兴奋总 量超过阈值 不应期 神经元被激发 进入兴奋状态 产生输出脉冲 由突触传递给其它神经元

2．生物神经元的工作机制 抑制状态的神经元 由树突和细胞体 接收传来的兴奋电位 不应期 产生输出脉冲 输入兴奋总 量超过阈值 神经元被激发 进入兴奋状态 由突触传递给其它神经元 7.2.1 基本概念 – 生物神经元

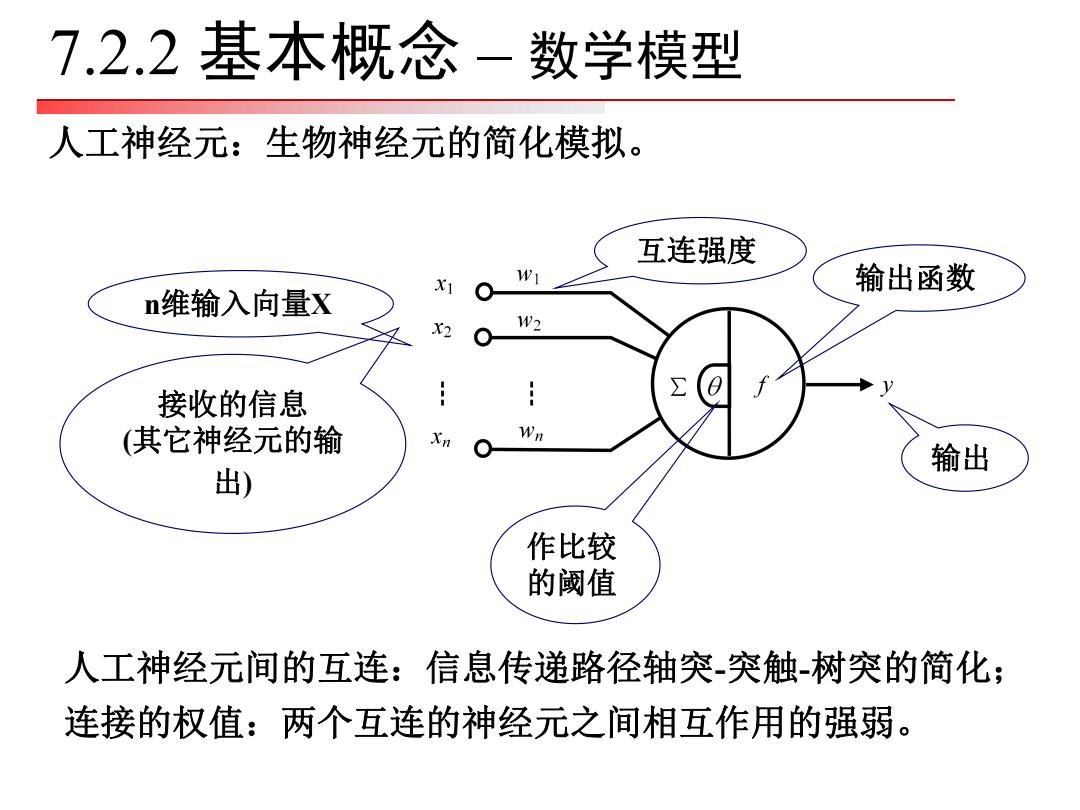
7.2.2基本概念-数学模型 人工神经元：生物神经元的简化模拟。 互连强度 X1 输出函数 n维输入向量X X2 W2 接收的信息 (其它神经元的输 Xn 输出 出) 作比较 的阈值 人工神经元间的互连：信息传递路径轴突-突触树突的简化； 连接的权值：两个互连的神经元之间相互作用的强弱

人工神经元：生物神经元的简化模拟。 人工神经元间的互连：信息传递路径轴突-突触-树突的简化； 连接的权值：两个互连的神经元之间相互作用的强弱。 接收的信息 (其它神经元的输 出) 互连强度 作比较 的阈值 n维输入向量X 输出 输出函数 7.2.2 基本概念 – 数学模型

7.2.2基本概念-数学模型 WI 0 >y=f(∑wixi-0) Wn 实际要复杂的多，该模型只是简化，是人工神经网络的基础！ 9

9 7.2.2 基本概念 – 数学模型 实际要复杂的多，该模型只是简化，是人工神经网络的基础！

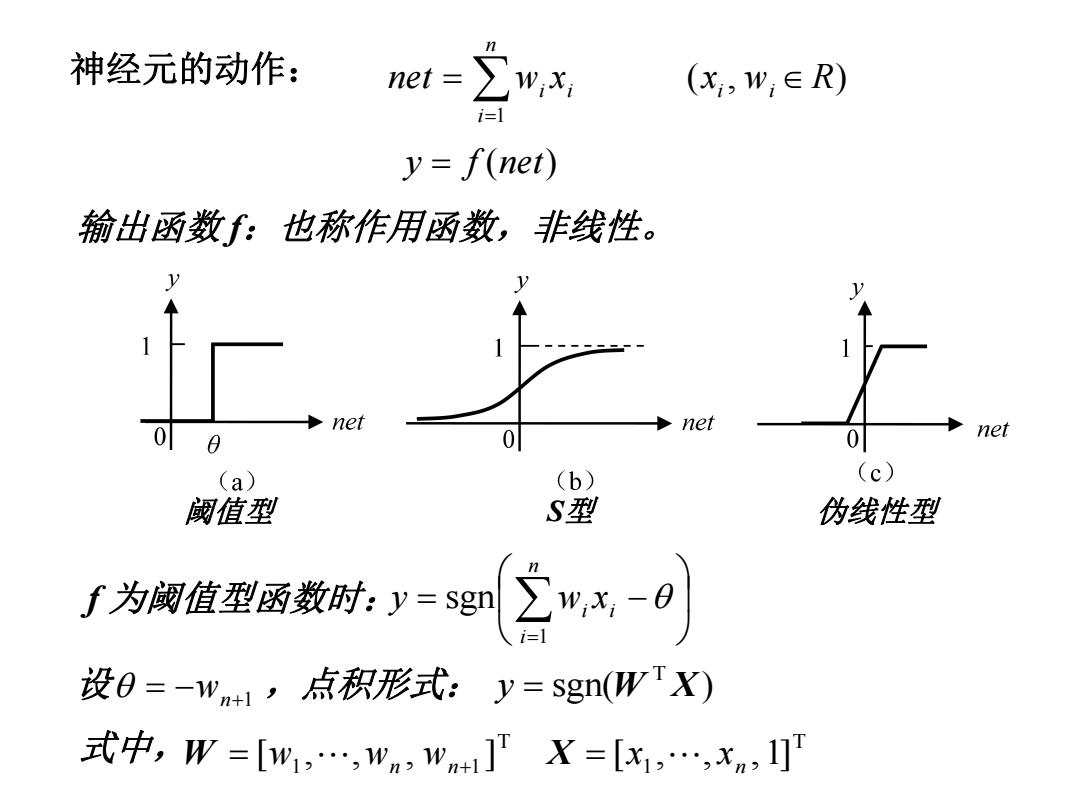
神经元的动作： net=∑w,x (X,W,∈R) i=1 y=f(net) 输出函数f:也称作用函数，非线性。 1 net net 0 0 0 net 0 (a) (b) (c) 阈值型 S型 伪线性型 f为侧位数所：=三x-0 设0=-wn+1，点积形式：y=sgn(WTX) 式中，W=[w1,…,wn,wn+1]X=[x1,…,xn,1]

神经元的动作：   n i i i net w x 1 y  f (net) (x , w R) i i  输出函数 f：也称作用函数，非线性。 阈值型 S型 伪线性型 f 为阈值型函数时：           n i i i y w x 1 sgn  设  wn1 ，点积形式： sgn( ) T y  W X T 1 1 [ , , , ] W  w  wn wn T 1 [ , , , 1] n 式中， X  x  x