
若图G中任意两个顶点 之间都有路径相通,则 称此图为连通图; 若无向图为非连通图 则图中各个极大连通子 图称作此图的连通分量
若图G中任意两个顶点 之间都有路径相通,则 称此图为连通图; 若无向图为非连通图, 则图中各个极大连通子 图称作此图的连通分量。 B A C D C F E D F B A E
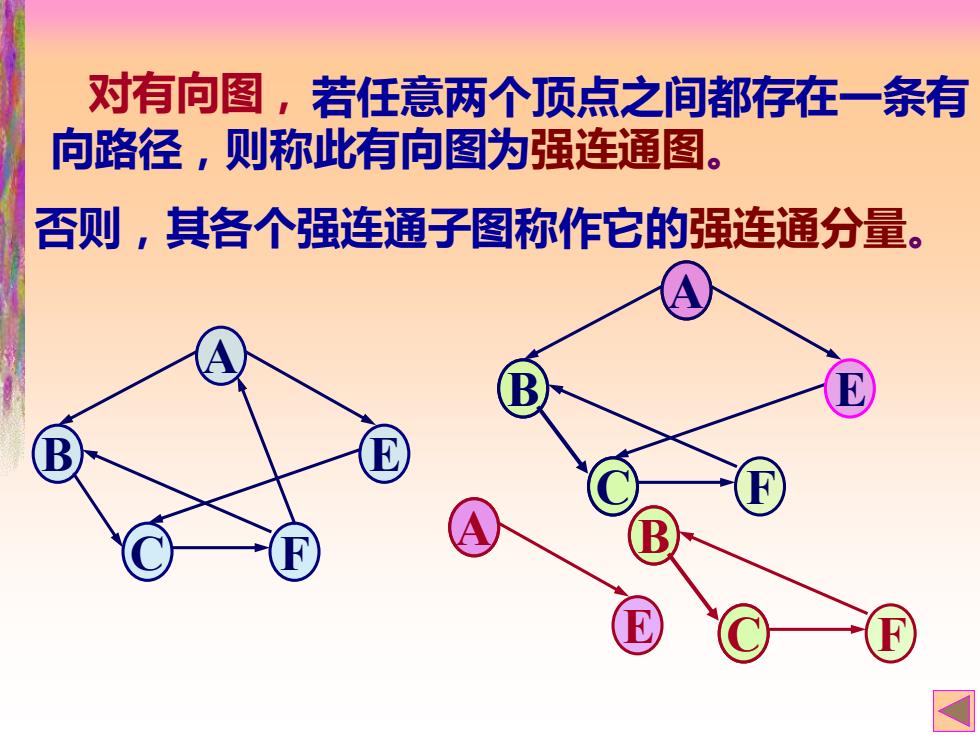
对有向图,若任意两个顶点之间都存在一条有 向路径,则称此有向图为强连通图。 否则,其各个强连通子图称作它的强连通分量
若任意两个顶点之间都存在一条有 向路径,则称此有向图为强连通图。 否则,其各个强连通子图称作它的强连通分量。 对有向图, A B E C F A B E C F A E B C F
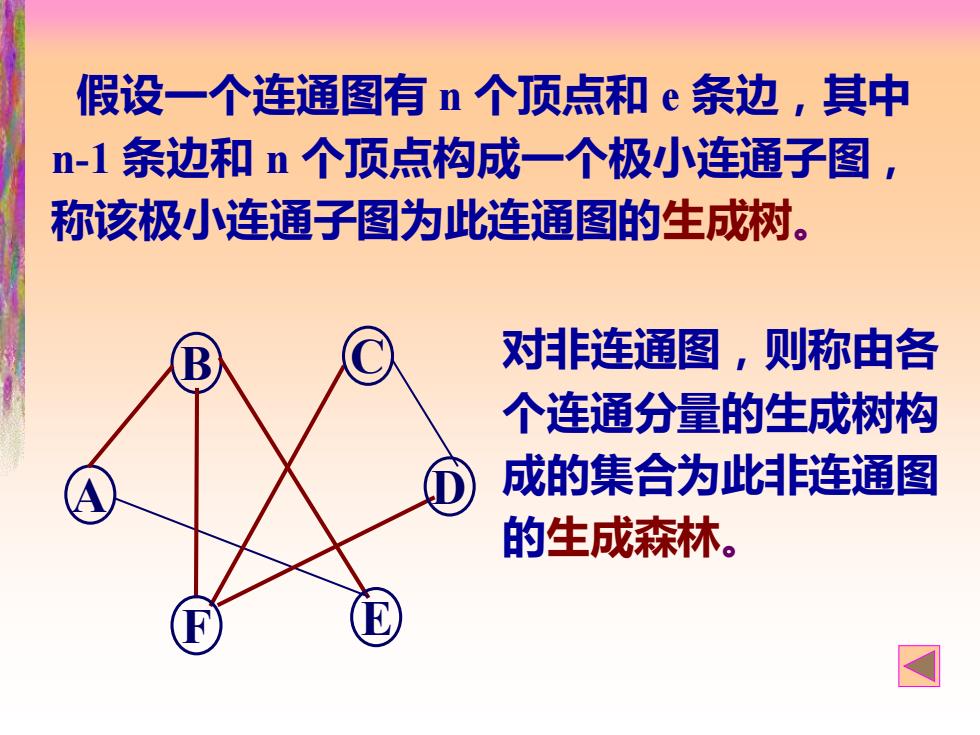
假设一个连通图有n个顶点和e条边,其中 n-1条边和n个顶点构成一个极小连通子图, 称该极小连通子图为此连通图的生成树。 对非连通图,则称由各 个连通分量的生成树构 成的集合为此非连通图 的生成森林
假设一个连通图有 n 个顶点和 e 条边,其中 n-1 条边和 n 个顶点构成一个极小连通子图, 称该极小连通子图为此连通图的生成树。 对非连通图,则称由各 个连通分量的生成树构 成的集合为此非连通图 的生成森林。 B A C D F E
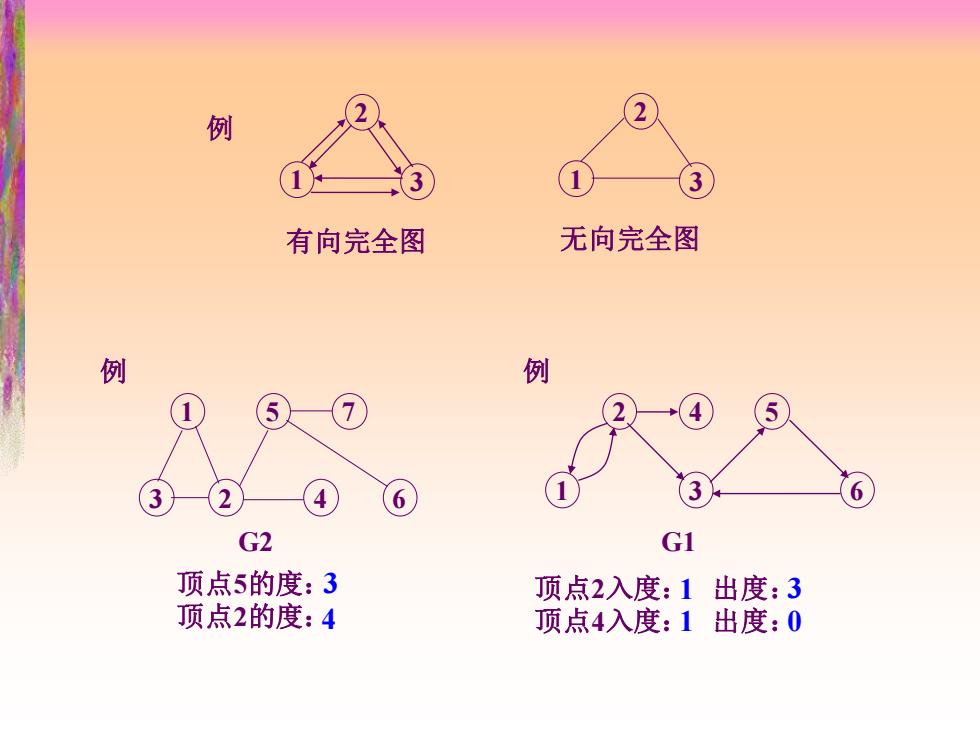
例 2 3 有向完全图 无向完全图 例 例 5 6 G2 G1 顶点5的度:3 顶点2入度:1出度:3 顶点2的度:4 顶点4入度:1出度:0
例 2 1 3 2 1 3 有向完全图 无向完全图 例 2 4 5 1 3 6 G1 顶点2入度: 出度: 顶点4入度: 出度: 例 1 5 7 3 2 4 G2 6 顶点5的度: 顶点2的度: 3 4 1 3 1 0

例 路径:1,2,3, 5,6,3 5 路径长度: 5 简单路径: 1,2,3,5,6 6 回路: 1,2,3,5, 6,3,1 简单回路:3,5,6,3 G1 例 5 路径:1,2,5,7,6,5,2,3 路径长度:7 简单路径:1,2,5,7,6 回路: 1,2,5,7,6,5,2,1 G2 简单回路:1,2,3,1
例 1 5 7 3 2 4 G2 6 例 2 4 5 1 3 6 G1 路径: 1 , 2 , 3 , 5 , 6 , 3 路径长度: 简单路径: 1 , 2 , 3 , 5 , 6 , 3 , 1 3 , 5 , 6 , 3 路径: 1 , 2 , 5 , 7 , 6 , 5 , 2 , 3 路径长度: 7 简单路径: 回路: 1 , 2 , 5 , 7 , 6 , 5 , 2 , 1 简单回路: 51 , 2 , 3 , 5 , 6 回路: 简单回路:1, 2 , 5 , 7 , 6 1 , 2 , 3 , 1