编泽原理 语法分析-自上而下分析 左递归的消除 墨假定关于非终结符P的规则为:P→Paβ 其中,B不以P开头。那么,我们可以把P的规则改写 为如下的非直接左递归形式: P→βP' P'→aPe 第引1页
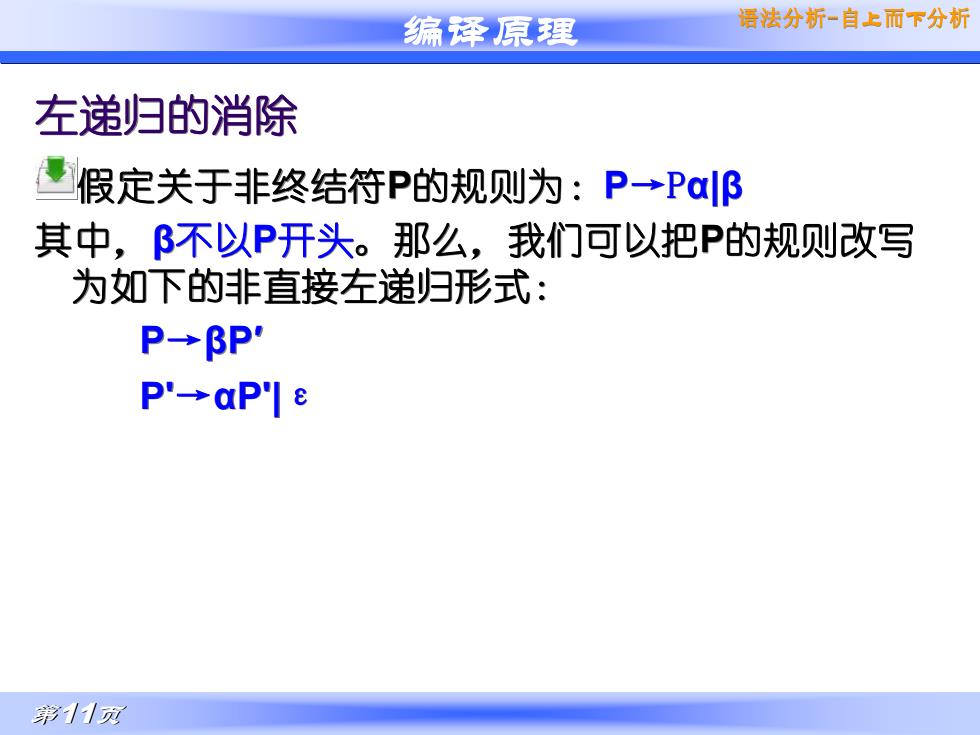
编译原理 第11页 语法分析-自上而下分析 左递归的消除 假定关于非终结符P的规则为:P→Pα|β 其中,β不以P开头。那么,我们可以把P的规则改写 为如下的非直接左递归形式: P→βP′ P'→αP'|ε

编泽原理 语法分折自上而下分析 墨例文法 E-E+TIT T→T*FF F→(E加 消除左递归 E→TE E+TE'l8 T-FT' T'→*FTIε F→(E加 第2列
编译原理 第12页 语法分析-自上而下分析 例文法 E→E+T|T T→T*F|F F→(E)|i 消除左递归 E→TE' E'→+TE'|ε T→FT' T'→*FT'| ε F→(E)|i
编泽原理 语法分析-自上而下分析 一般情况 P-→PaPa2l.Pamlβ1lB2lBn 消除P的左递归 P→β1P'I2PlβnP' P a1 P'l a2 P'l...Jam P'l 第13页
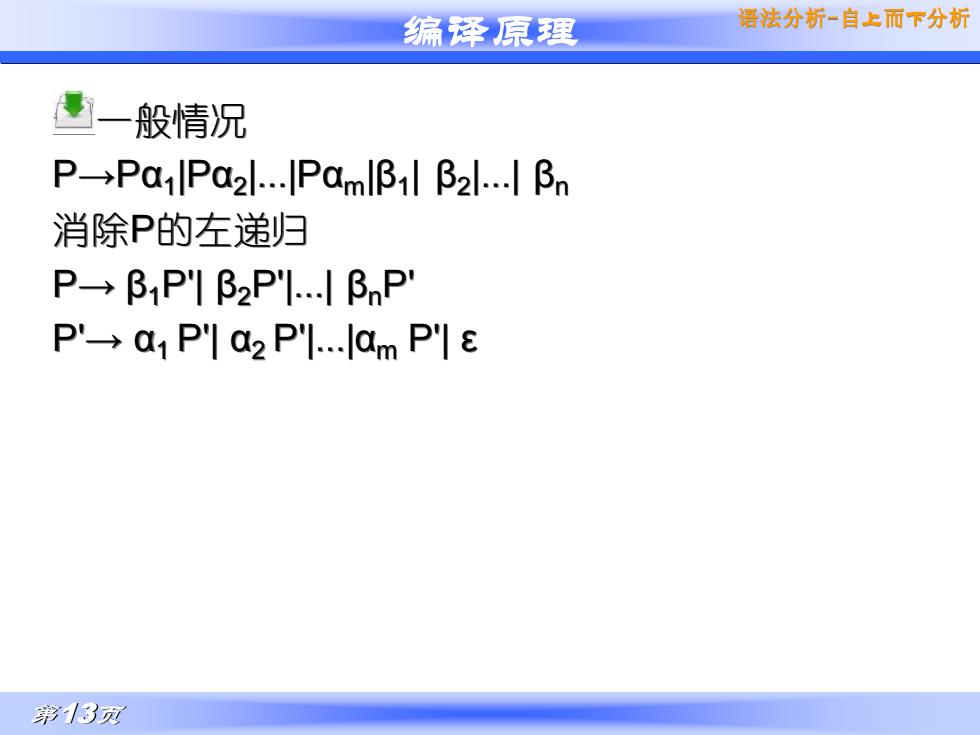
编译原理 第13页 语法分析-自上而下分析 一般情况 P→Pα1 |Pα2 |...|Pαm|β1 | β2 |...| βn 消除P的左递归 P→ β1P'| β2P'|...| βnP' P'→ α1 P'| α2 P'|...|αm P'| ε

编泽原理 语法分折-自上而下分析 间接左递归 量例如文法: SQclc QRblb R-Sala 虽不具有直接左递归,但S,Q,R都是左递归的,例如有 S=>Qc=>Rbc=>Sabc 第苑
编译原理 第14页 语法分析-自上而下分析 间接左递归 例如文法 : S →Qc|c Q →Rb|b R →Sa|a 虽不具有直接左递归,但S,Q,R都是左递归的,例如有 S=>Qc=>Rbc=>Sabc
编译原理 语法分析-自上而下分析 消除左递归方法: (1)将间接左递归改造为直接左递归 将文法中所有如下形式的产生式: P→PYlβlβ2Bn P1→δlδ2l53l.δk 改写成: P→δYlδ2yIδ3l.δkylβlβ2l.βn 第15页
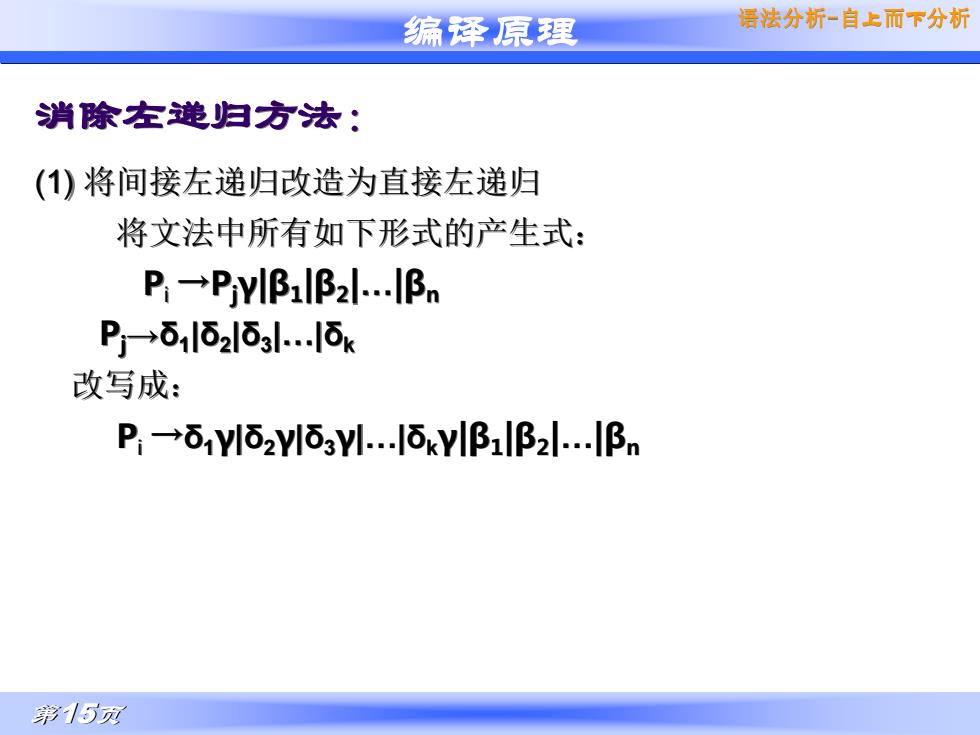
编译原理 第15页 语法分析-自上而下分析 消除左递归方法: (1) 将间接左递归改造为直接左递归 将文法中所有如下形式的产生式: Pi →Pjγ|β1 |β2 |…|βn Pj→δ1 |δ2 |δ3 |…|δk 改写成: Pi →δ1γ|δ2γ|δ3γ|…|δkγ|β1 |β2 |…|βn