
例 PCA主成分分析 KL变换 电子科技大学研究生《模式识别》
电子科技大学研究生《模式识别》 PCA主成分分析 KL变换
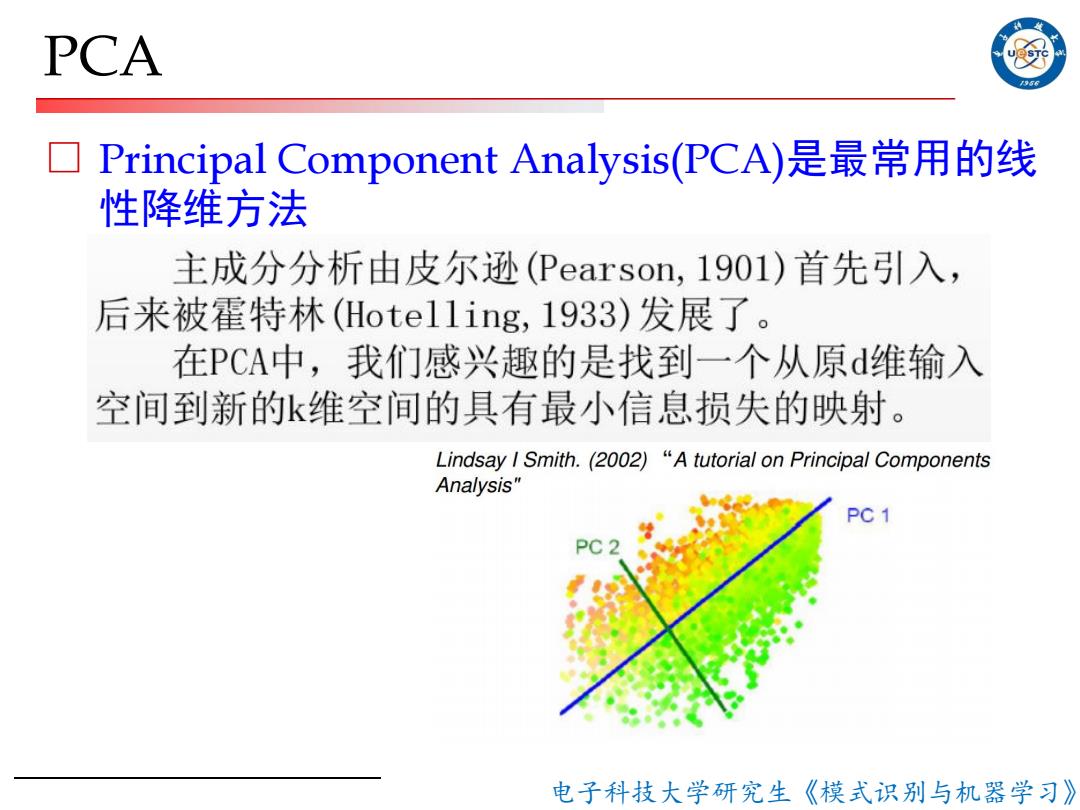
PCA 号5 Principal Component Analysis(PCA)是最常用的线 性降维方法 主成分分析由皮尔逊(Pearson,1901)首先引入, 后来被霍特林(Hote11ing,1933)发展了。 在PCA中,我们感兴趣的是找到一个从原d维输入 空间到新的k维空间的具有最小信息损失的映射。 Lindsay I Smith.(2002)"A tutorial on Principal Components Analysis" PC 1 电子科技大学研究生《模式识别与机器学习》
电子科技大学研究生《模式识别与机器学习》 PCA □ Principal Component Analysis(PCA)是最常用的线 性降维方法

PCA计算流程 56 口1)获取数据 ☐2)减去均值 ☐3)i 计算协方差矩阵 口4)计算协方差矩阵的特征矢量和特征值 ☐5)选择特征值最大的K个特征值对应的特征向量 作为主成分 口6)用主成分矩阵乘以原始数据得到降维后的数据 电子科技大学研究生《模式识别与机器学习》
电子科技大学研究生《模式识别与机器学习》 PCA □ 1)获取数据 □ 2)减去均值 □ 3)计算协方差矩阵 □ 4)计算协方差矩阵的特征矢量和特征值 □ 5)选择特征值最大的K个特征值对应的特征向量 作为主成分 □ 6)用主成分矩阵乘以原始数据得到降维后的数据 计算流程
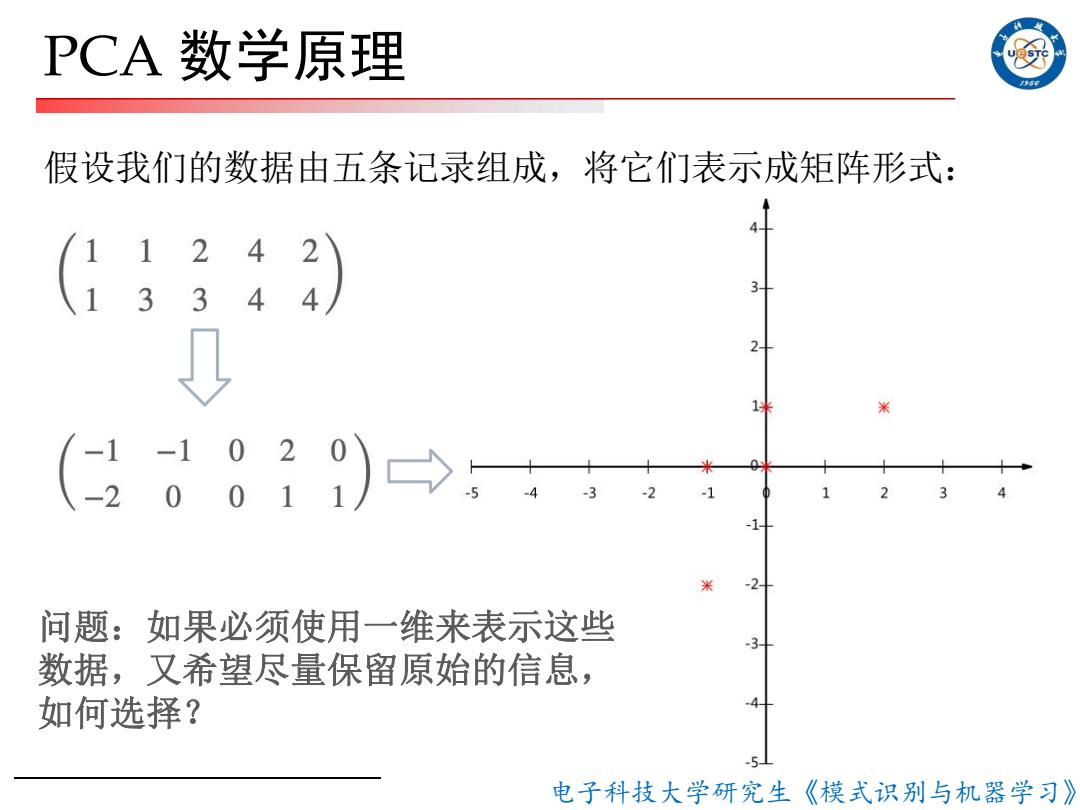
PCA数学原理 956 假设我们的数据由五条记录组成,将它们表示成矩阵形式: 1 4 2 2 问题:如果必须使用一维来表示这些 数据,又希望尽量保留原始的信息, 如何选择? 电子科技大学研究生《模式识别与机器学习》
电子科技大学研究生《模式识别与机器学习》 PCA 数学原理 假设我们的数据由五条记录组成,将它们表示成矩阵形式: 问题:如果必须使用一维来表示这些 数据,又希望尽量保留原始的信息, 如何选择?
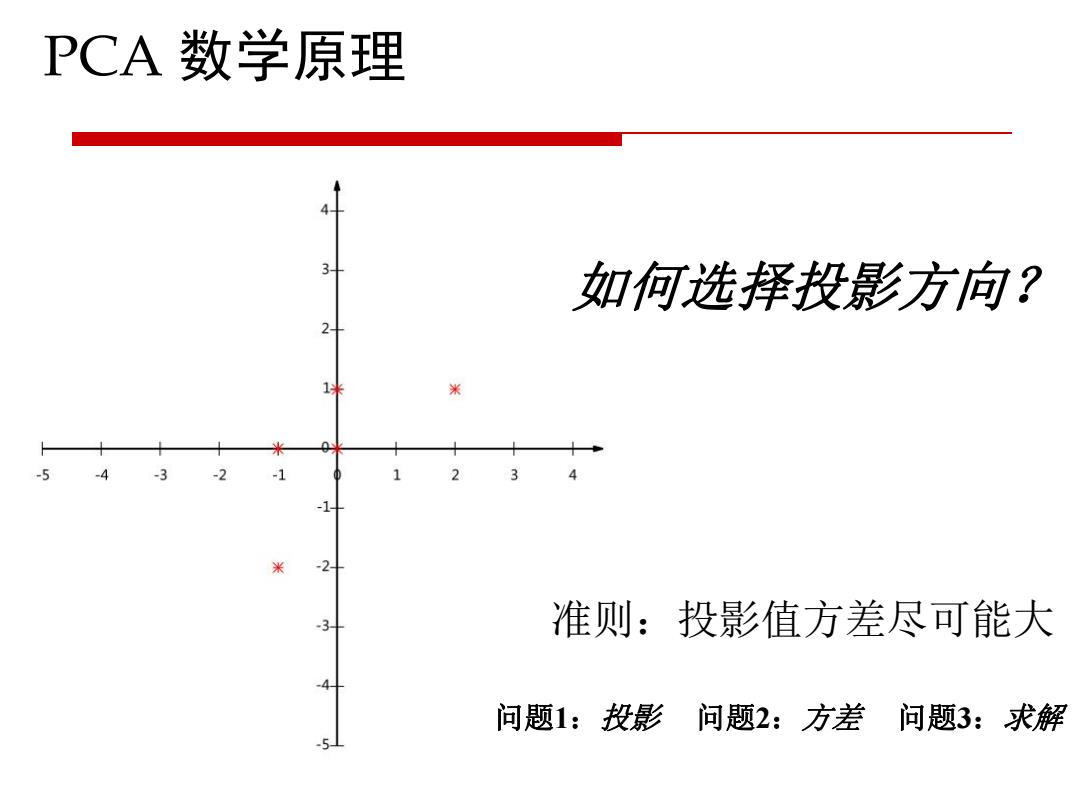
PCA数学原理 如何选择投影方向? 准则:投影值方差尽可能大 问题1:投影 问题2:方差问题3:求解
PCA 数学原理 如何选择投影方向? 准则:投影值方差尽可能大 问题1:投影 问题2:方差 问题3:求解