
最近邻法的渐进错误率 假设在三类问题中,x的后验概率分别为 P(01x)=0.4 P(02x)=0.3P(03x)=0.3 按最小错误率的Bayes?决策法则:以概率1决策r∈O; 按最近邻决策法则:以概率P(ox)=0.4决策x∈01;以 概率1-P(01x)=0.6决策x廷。 当P(omx)≈I时,最近邻法的决策结果与最小错误率的 Bayest决策的决策结果相同,它们的错误率都是比较小 的,两种方法同样的好,当P(omx)=1,两者的错误 概率接近于1-1,两种方法同样的坏
x 1 2 3 P( x)0.4 P( x)0.3 P( x)0.3 x1 1 P( x)0.4 x1 1 1 P( x)0.6 x1 P(m x)1 1 P( m ) c x 1 1 c 最近邻法的渐进错误率

最近邻法 距离度量可以换成相似性度量,相似度最大 适用于样本数足够多的情况 ● 样本数目太少,带有很大的偶然性,影响方法的 性能 很多情况下,把决策建立在一个最近的样本上有 一定危险
• 距离度量可以换成相似性度量,相似度最大 • 适用于样本数足够多的情况 • 样本数目太少,带有很大的偶然性,影响方法的 性能 • 很多情况下,把决策建立在一个最近的样本上有 一定危险 最近邻法

K-近邻法 口近邻法的很自然的改进一投票机制 k=7 k=3 18
o 近邻法的很自然的改进—投票机制 K-近邻法 18

K-近邻法 口近邻法的很自然的改进一投票机制 k-近邻法(kNN) 找出x的k个近邻,看其中多数属于哪一类,则把x分到哪一类。 一般表示:c类o,i=1,…,c,N个样本。 k;,i=1,…,c为x的k个近邻中属于o,的样本数 判别函数:g,(x)=k,i=1…,0 决策规则:ifg,()=maxk,then∈0 1*
K-近邻法 o 近邻法的很自然的改进—投票机制
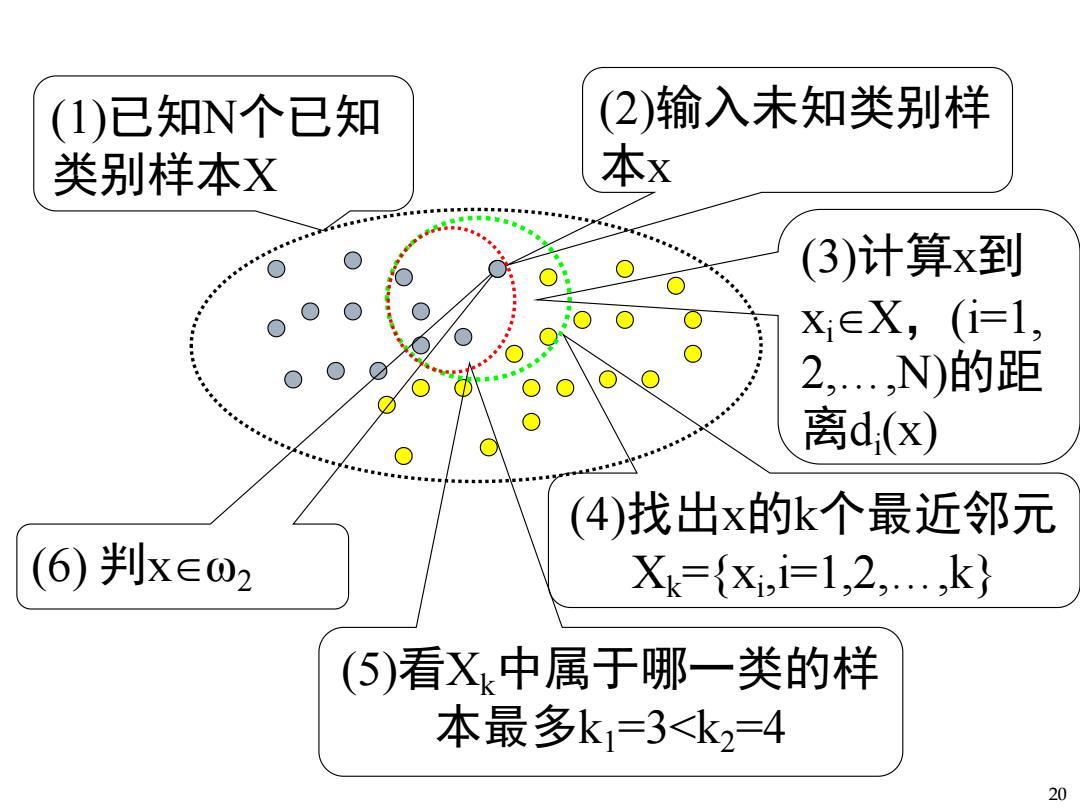
(1)已知N个已知 (2)输入未知类别样 类别样本X 本x (3)计算x到 x∈X,(i=1, 2,..N)的距 离d(x) ■ (4)找出x的k个最近邻元 (6)判x∈02 Xk={X1,i=1,2,.,k} (5)看Xk中属于哪一类的样 本最多k1=3<k2=4 20
20 (1)已知N个已知 类别样本X (2)输入未知类别样 本x (6) 判xω2 (4)找出x的k个最近邻元 Xk={xi,i=1,2,…,k} (5)看Xk中属于哪一类的样 本最多k1=3<k2=4 (3)计算x到 xiX,(i=1, 2,…,N)的距 离di(x)