S1 10 10 2 2 3 S2 S2 5 5 5 8 8 6 00 6 00 3 12 20 20 1 1 6 13 13 54 SA 8 品 11 2 % 85

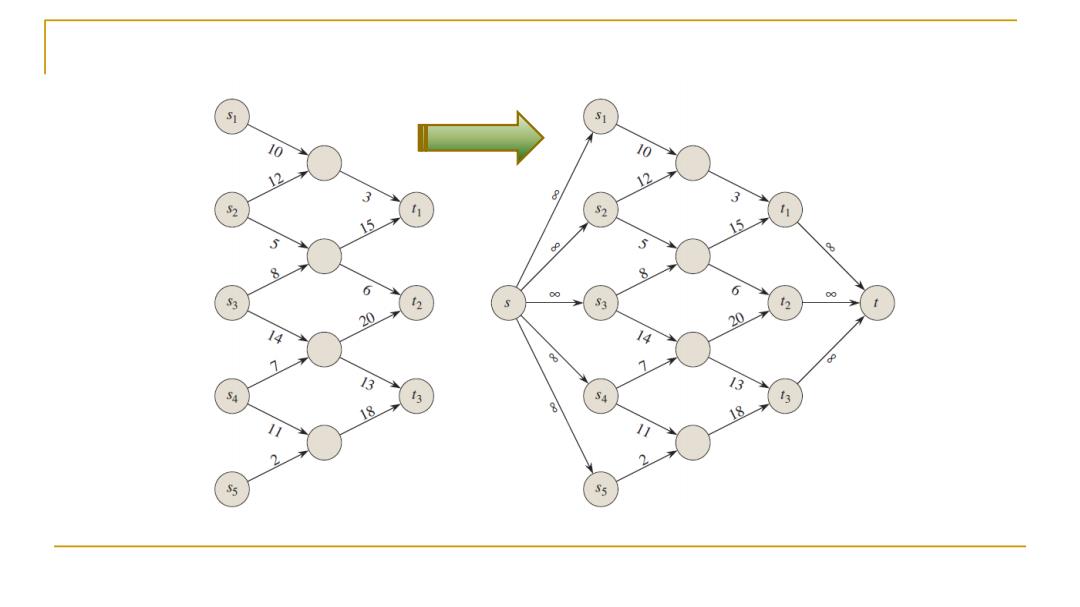
严格的数学模型 We are now ready to define flows more formally.Let G =(V,E)be a flow network with a capacity function c.Let s be the source of the network,and let t be the sink.A flow in G is a real-valued function f:Vx V->R that satisfies the following two properties: Capacity constraint: Flow conservation:For all u V-fs.t,we require When (u,v)E,there can be no flow from u to v,and f(u,v)=0
严格的数学模型

问题4: 什么叫一个flow的value? If1=∑fs,)-∑fu,) ve y 什么是最大流问题?
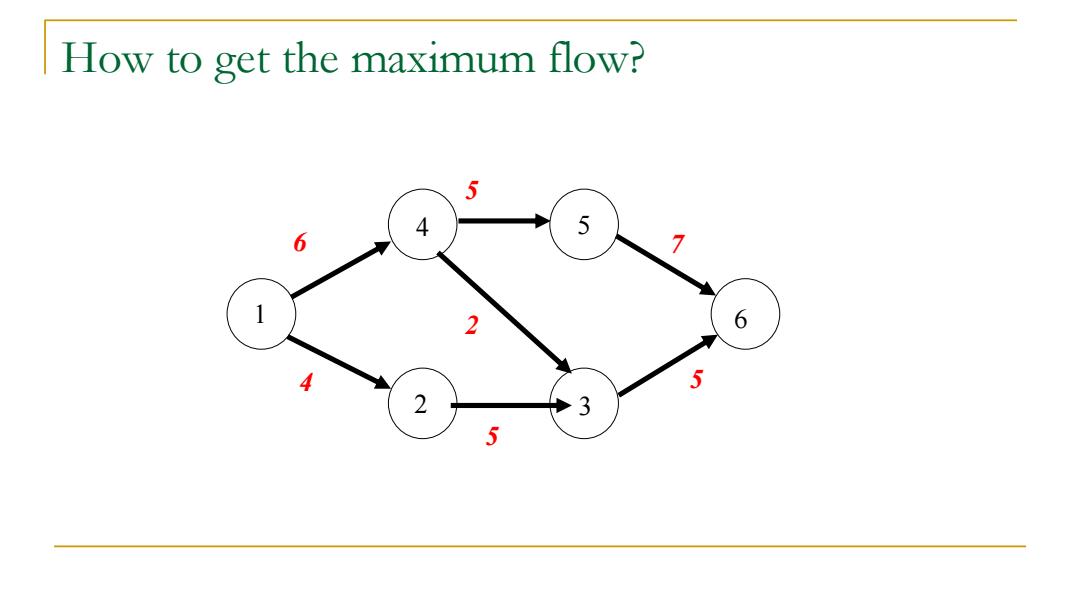
How to get the maximum flow? 5 4 5 6 2 6 4 5 2 3 5
How to get the maximum flow? 6 4 5 2 3 1 5 5 4 7 5 6 2
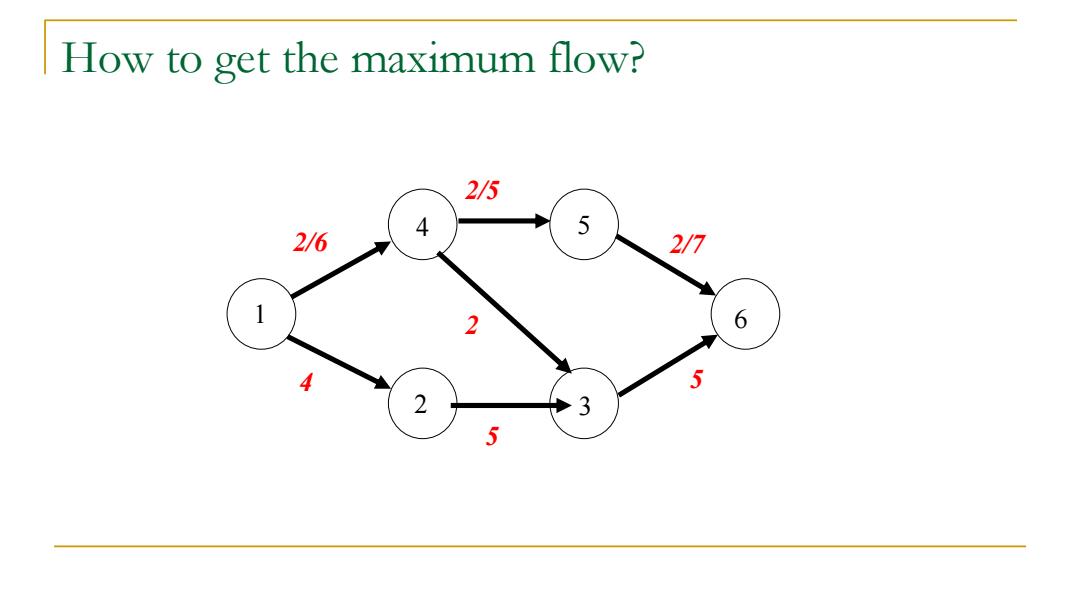
How to get the maximum flow? 2/5 4 5 2/6 2/7 2 6 4 5 2 3 5
How to get the maximum flow? 6 4 5 2 3 1 5 5 4 2/7 2/5 2/6 2