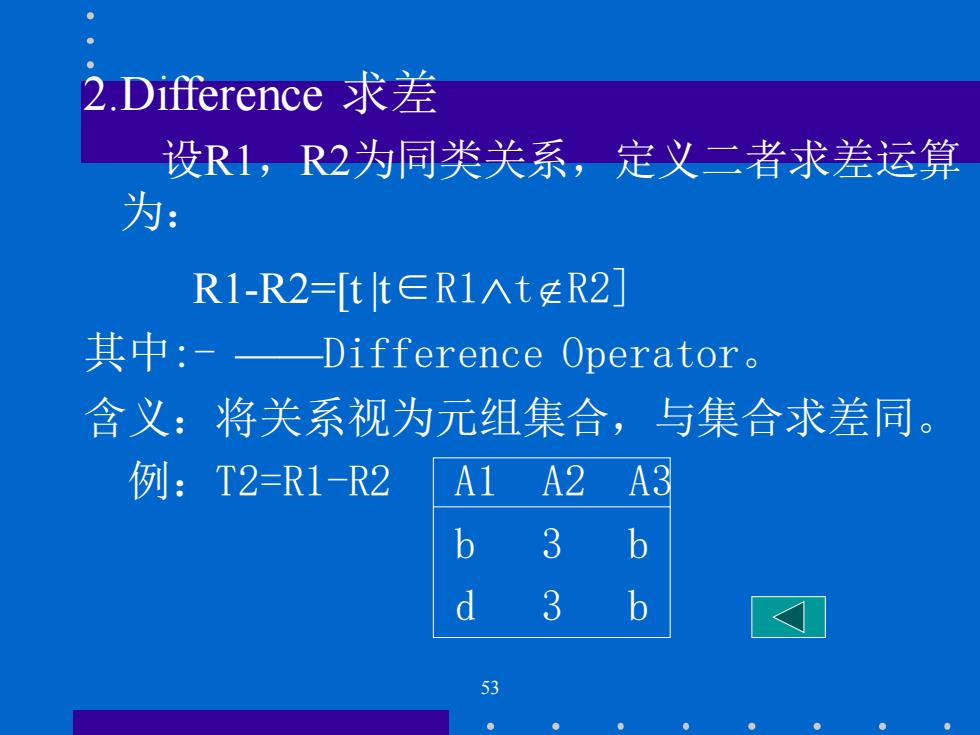
2.Difference求差 设R1,R2为同类关系,定义二者求差运算 为: R1-R2=[tt∈R1入teR2] 其中:-—Difference Operator。 含义:将关系视为元组集合,与集合求差同。 例:T2=R1-R2 A1 A2 A3 b 3 b d 3 53
53 2.Difference 求差 设R1,R2为同类关系,定义二者求差运算 为: R1-R2=[t |t∈R1tR2] 其中:- ——Difference Operator。 含义:将关系视为元组集合,与集合求差同。 例:T2=R1-R2 A1 A2 A3 b 3 b d 3 b

3 Product求积 设:R为K1度关系,S为K2度关系定义二者乘 积: RxS=[tt=<1,tk2>Atk1∈RAtk2∈S] 其中:X-Product Operator 含义:设R有N1个元组,S有N2个元组,将 R,S分别视为N1,N2重有序组,RxS与两个 有序组笛卡尔积同意义。 54
54 3.Product 求积 设:R为K1度关系,S为K2度关系.定义二者乘 积: RS=[t|t=<tk1,tk2>t k1∈R t k2 ∈S] 其中:X-Product Operator 含义:设R有N1个元组,S有N2个元组,将 R,S分别视为N1,N2重有序组,RS与两个 有序组笛卡尔积同意义
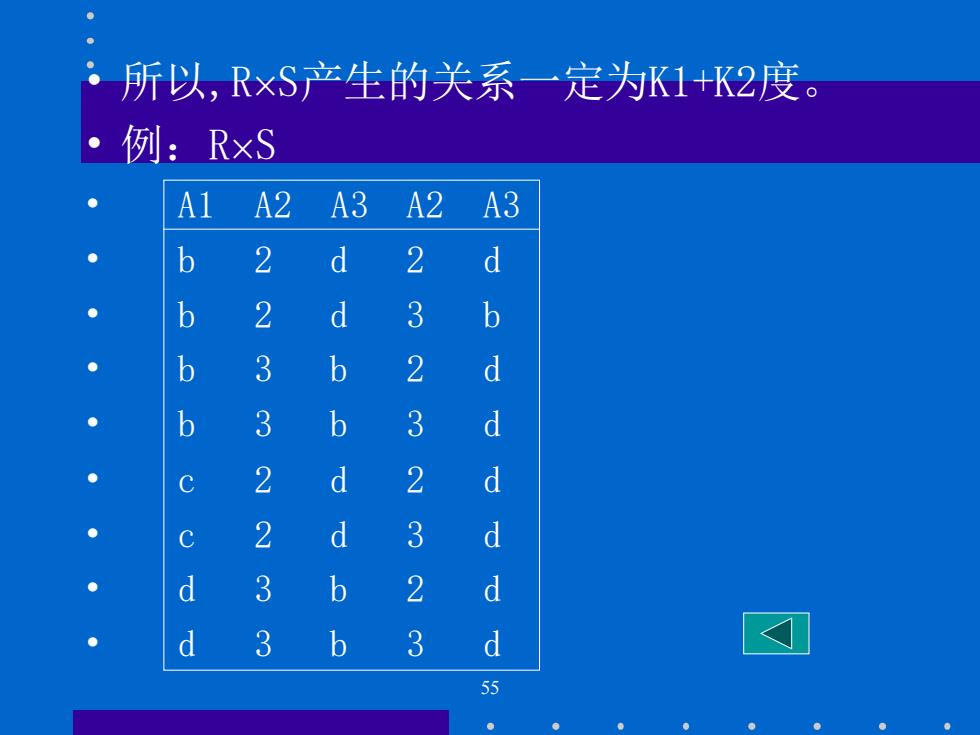
所以,RxS产生的关系一定为K1+K2度。 ·例:RxS A1 A2 A3 A2 A3 b 2 d b 2 3 b b 3 2 d b 3 3 d 2 d C 2 d 3 d d 3 b 2 d d 3 b 3 d 团 55
55 • 所以,RS产生的关系一定为K1+K2度。 • 例:RS • A1 A2 A3 A2 A3 • b 2 d 2 d • b 2 d 3 b • b 3 b 2 d • b 3 b 3 d • c 2 d 2 d • c 2 d 3 d • d 3 b 2 d • d 3 b 3 d