
离心力FN在微弧段两端会产生拉力Fc。 da 由力平衡条件得: da 取sin da 2 da,得 2 c=qv- N 离心力只发生在带作圆周运动的部分 但由此引起的拉力确作用在带的全长: 离心拉应力: 0e= E= 91 MPa
新疆大学专用 作者: 潘存云教授 设计:潘存云 离心力 FNc在微弧段两端会产生拉力 Fc。 qv da da Fc 2 2 由力平衡条件得: 2 sin = dFNc dα dl r F1 F2 Fc Fc dα 2 dα 2 : 2 2 取sin ,得 da da Fc qv N 2 = MPa A qv A Fc c 2 = = 离心力只发生在带作圆周运动的部分, 但由此引起的拉力确作用在带的全长。 离心拉应力: 往x轴投影
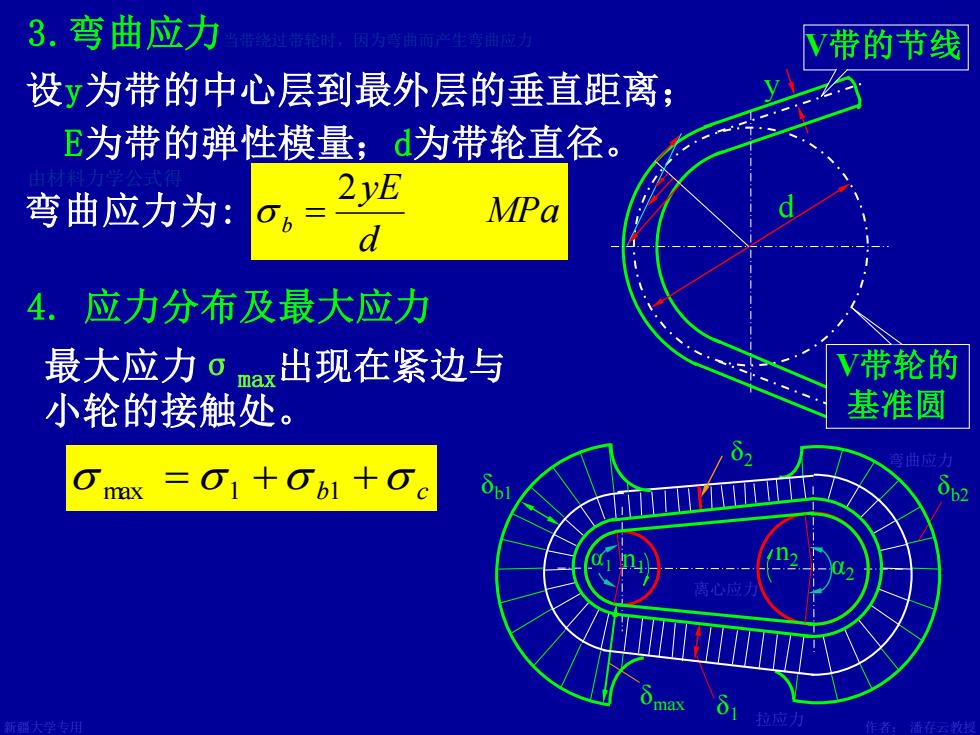
3.弯曲应力 带路刘带量时,因为是曲而产生弯油应力 V带的节线 设y为带的中心层到最外层的垂直距离; E为带的弹性模量;d为带轮直径。 弯曲应力为: 2yE MPa d 4.应力分布及最大应力 最大应力oax出现在紧边与 V带轮的 小轮的接触处。 基准圆 bl 离心应 0 作者:潘存云教
新疆大学专用 作者: 潘存云教授 设计:潘存云 设计:潘存云 3.弯曲应力当带绕过带轮时,因为弯曲而产生弯曲应力 MPa d yE b 2 = 设y为带的中心层到最外层的垂直距离; E为带的弹性模量;d为带轮直径。 4. 应力分布及最大应力 δmax δ1 δb2 α2 n1 α1 n2 max = 1 + b1 + c δb1 δ2 y 弯曲应力为: 最大应力σmax出现在紧边与 小轮的接触处。 V带的节线 d V带轮的 基准圆 由材料力学公式得 离心应力 拉应力 弯曲应力
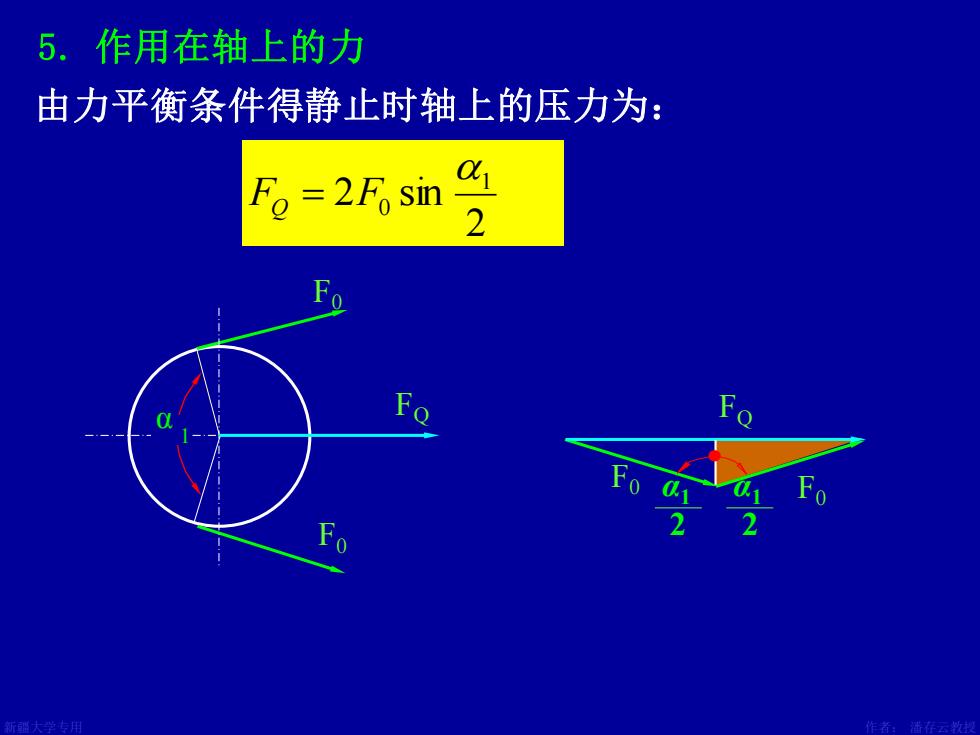
5.作用在轴上的力 由力平衡条件得静止时轴上的压力为: Fo =2Fosin 0 0
新疆大学专用 作者: 潘存云教授 设计:潘存云 设计:潘存云 F0 F0 α 1 由力平衡条件得静止时轴上的压力为: 5. 作用在轴上的力 FQ F0 F0 FQ 2 2 sin 1 0 FQ = F α1 2 α1 2

§13-4 带传动的弹性滑动和传动比 设带的材料符合变形与应力成正比的规律,则变形量为: 紧边: 松边: F 2 AE AE F1>F2 £2 带绕过主动轮时,将逐渐缩 短并沿轮面滑动,使带速落 主动轮 后于轮速。 从动轮 带经过从动轮时,将逐渐被拉长并沿轮面滑动,使带 速超前于轮速。 这种因材料的弹性变形而产生的滑动被称为弹性滑动。 πdn πd2n2 N m/s 60×1000 60×1000 m/s总有:2<
新疆大学专用 作者: 潘存云教授 设计:潘存云 F2 F2 F1 F1 §13-4 带传动的弹性滑动和传动比 设带的材料符合变形与应力成正比的规律,则变形量为: 这种因材料的弹性变形而产生的滑动被称为弹性滑动。 紧边: 松边: AE F1 1 = AE F2 2 = ∵ F1 > F2 ∴ ε1 > ε2 带绕过主动轮时,将逐渐缩 短并沿轮面滑动,使带速落 后于轮速。 带经过从动轮时,将逐渐被拉长并沿轮面滑动,使带 速超前于轮速。 m s d n v / 60 1000 1 1 1 = m s d n v / 60 1000 2 2 2 = 总有:v2 < v1 从动轮 n2 主动轮 n1

=y- din-din 定义: 为滑动率。 V dn 得从动轮的转速: nd1(1-) n2= d, 带传动的传动比: n n2 d(1-E) V带传动的滑动率e=0.010.02,一般可忽略不计
新疆大学专用 作者: 潘存云教授 得从动轮的转速: 带传动的传动比: 2 1 1 2 (1 ) d n d n − = (1 ) 1 2 − = d d 2 1 n n i = V带传动的滑动率ε=0.01~0.02,一般可忽略不计。 定义: 1 1 1 1 2 2 1 1 2 d n d n d n v v v − = − = 为滑动率