
淘汰部分显性类型的随机交配群体 淘汰率(S)=选择系数 留种率=适合度=1S eg:牛角的有无,无角为显性,有角为隐性。 PP Pp pp 无角 有角 设:原始群体的基因型频率: D=p2 H=2pq R=g 淘汰率为S,所以留种率=1一S
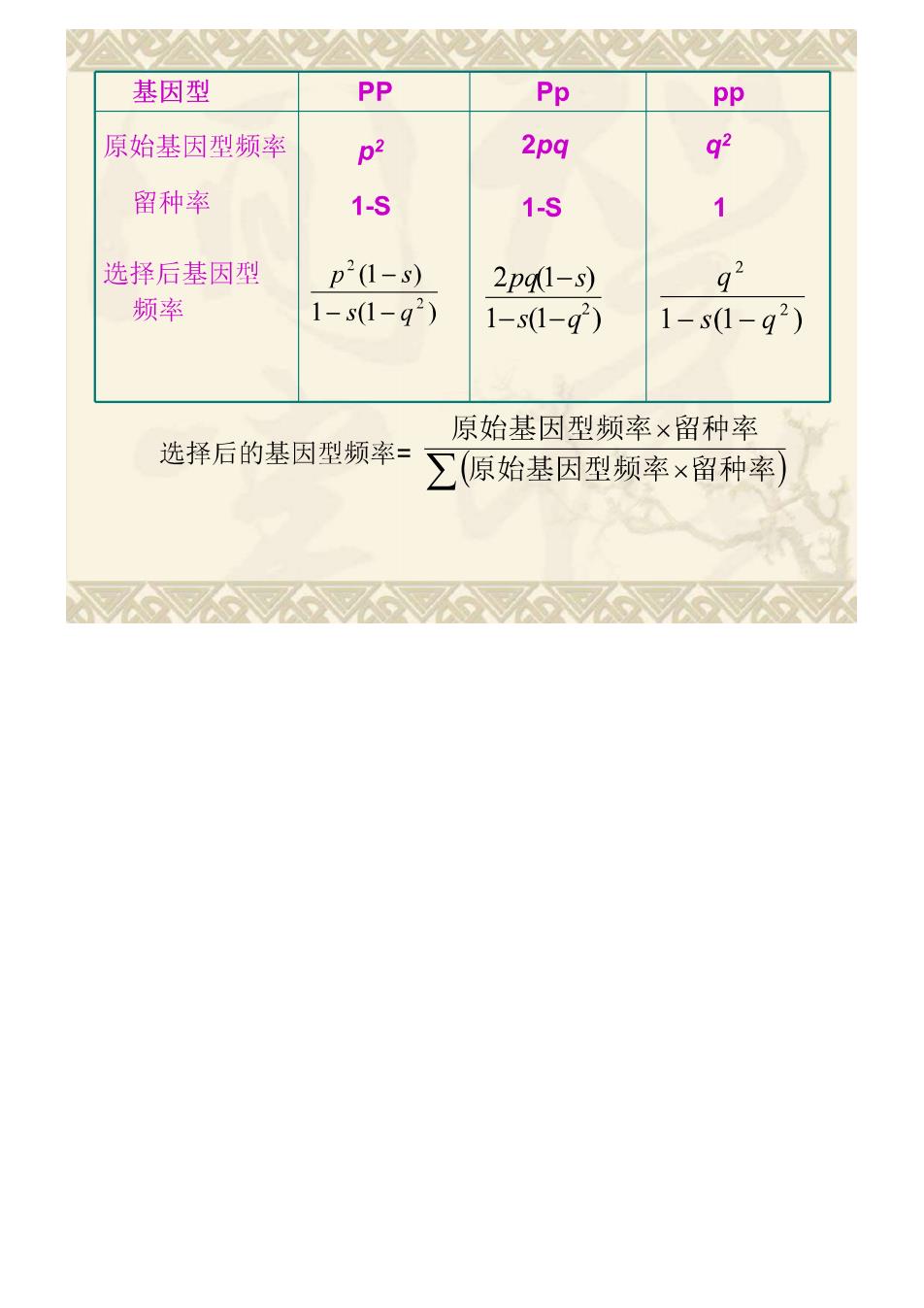
基因型 PP Pp pp 原始基因型频率 p2 2pq 9 留种率 1-S 1-S 1 选择后基因型 p2(1-s) 2p1-s) 92 频率 1-s(1-42) 1-s1-q) 1-s1-q2) 原始基因型频率×留种率 选择后的基因型频率= ∑原始基因型频率×留种率)

上式分母=p21-S)+2p91-S)+g2 =1-S1-q2) 设选择后的基因型频率分别为D、H'、R D'= p21-s) H= 2pq(1-s) 1-s1-q2) 1-s1-g2) R=- 1-s(1-92)

9-s(g-q2) 选择后隐性基因频率 9= 1-s(1-q) 若:S=1,则q=1;经过一代选择,群体固定 (条件:外显率为100%) S=0,则q=q,此时群体处于自然平衡状态 结论:隐性基因的选择比较容易实现

例愿:有个648只的山羊群体中,其中471识表现为无角,现 淘汰了86只,问下一代隐性基因的频率是多少?(为什么要淘汰 无角,因为间性羊在无角羊中出现,且基因为连锁基因)无一有 解:由已知可得: 有角羊的基因型频率 R-648-471=0.27 648 有角羊的基因频率 9=VR=√0.27=0.52 无角羊的淘汰率 S=86 =0.18 471 下一代隐性基因的频率为: 4=g-Sg-42)_027-0180.520.27=055 1-S1-9) 1-0.18(1-0.27) 如此可逐步淘汰间性羊,此方法可用于对经济性状无重大影响的基因的选择