
PARAMETERIZE SOURCE/SINK MECHANISMS W 2x c [M/T] [L3T][ML31 kx Vx c /T][L3JIM/L3] v x Ax c L/T]LJM/L3]
W [M/T] Q x c [L3 /T][M/L3 ] k x V x c [/T][L3 ][M/L3 ] v x A x c [L/T] [L2 ][M/L3 ] PARAMETERIZE SOURCE/SINK MECHANISMS
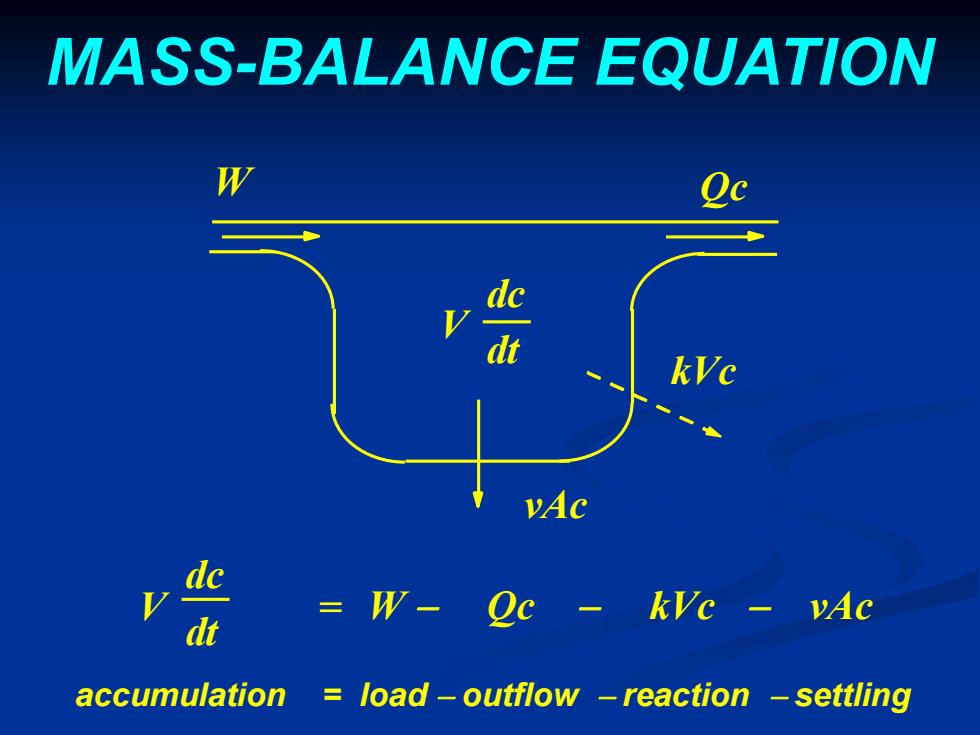
MASS-BALANCE EQUATION W vAc W- VAc dt Qc accumulation load-outflow -reaction -settling
W Qc kVc vAc V dc dt V dc dt = accumulation = load outflow reaction settling MASS-BALANCE EQUATION W Qc kVc vAc

THE FINAL MODEL A single,linear,first-order,nonhomogeneous ordinary differential equation dc =W-Oc-kVc-vAc dt dependent Canonical form: variable +K forcing independent function variable parameters
THE FINAL MODEL V dc dt = W Qc kVc vAc A single, linear, first-order, nonhomogeneous ordinary differential equation dc dt Q V k v H c W V dependent variable independent variable parameters forcing function Canonical form:

SOLUTIONS Steady-state (Accumulation 0) What happens if we subject a system to constant conditions for a sufficiently long period?What will be the stable state? Time-variable or transient solutions Given an initial condition,how will the system change temporally?
Steady-state (Accumulation = 0) What happens if we subject a system to constant conditions for a sufficiently long period? What will be the stable state? SOLUTIONS Time-variable or transient solutions Given an initial condition, how will the system change temporally?

STEADY-STATE SOLUTION =W-Oc kVc -vAc Forcing function (The“external' world) C= Q+kV+vA Purging parameters (physics,chemistry, biology)
STEADY-STATE SOLUTION V dc dt = W Qc kVc vAc 0 Forcing function (The “external” world) Purging parameters (physics, chemistry, biology) c W Q kV vA