
5.2多段图问题 1.问题的描述 ●在多段图中求从s到t的一条最小成本的路径,可以看作 是在k-2个段作出某种决策的结果。 ●第次决策决定V+1中的哪个结点在这条路径上,这里 1≤i≤k-2; ●最优性原理对多段图问题成立 2023/4/28
2023/4/28 5.2 多段图问题 1. 问题的描述 ● 在多段图中求从s到t的一条最小成本的路径,可以看作 是在k-2个段作出某种决策的结果。 ● 第i次决策决定Vi+1中的哪个结点在这条路径上,这里 1≤i≤k-2; ● 最优性原理对多段图问题成立

2.向前处理策略求解 设P(,)是一条从V中的结点到汇点t的最小成本路径, COST(,j)是这条路径的成本。 )向前递推式 COST(i,j)=min c(j,1)+COST(i+1,)) 2)递推过程 E ★第k-1段 c0,t)<j,t>∈E COST(k-1.j)= ∞<j,t>庆E ★j∈Vk-2计算CoST(k-2,j)=min{c0,)+cost(k-1,)} ★C0ST(1,S) l∈Vk-i <j,1>∈E(G) 2023/4/28
2023/4/28 2. 向前处理策略求解 设 P(i,j)是一条从Vi中的结点j到汇点t的最小成本路径, COST(i,j)是这条路径的成本。 1) 向前递推式 2) 递推过程 ★ 第k-1段 c(j,t) <j,t>∈E COST(k-1,j) = ∞ ★ j∈VK-2计算COST(k-2,j)=min{c(j,l)+cost(k-1,l)} ★ COST(1,S) ( , ) min { ( , ) ( 1, )} ( , ) 1 COST i j c j l COST i l j l E l vi = + + + j,t E , ( ) 1 j l E G l vk −
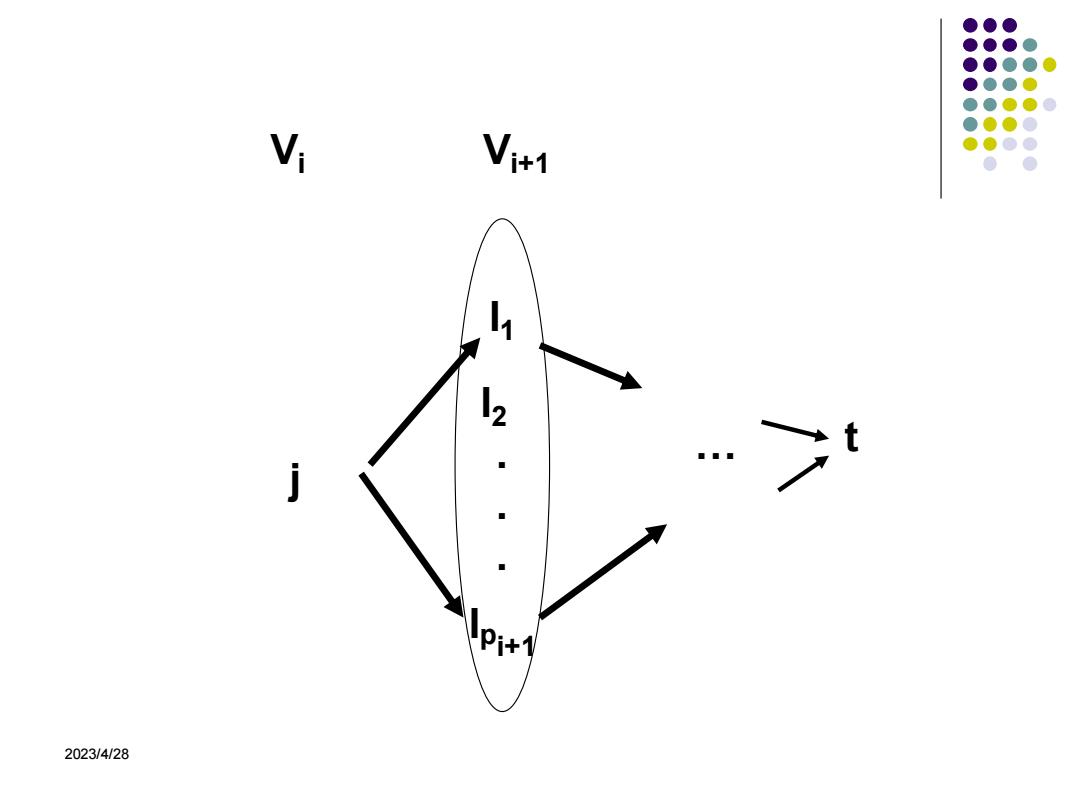
●● Vi Vi+1 11 2 …t Pi+1 2023/4/28
2023/4/28 l 1 l 2... l pi+1 … t j V i Vi+1
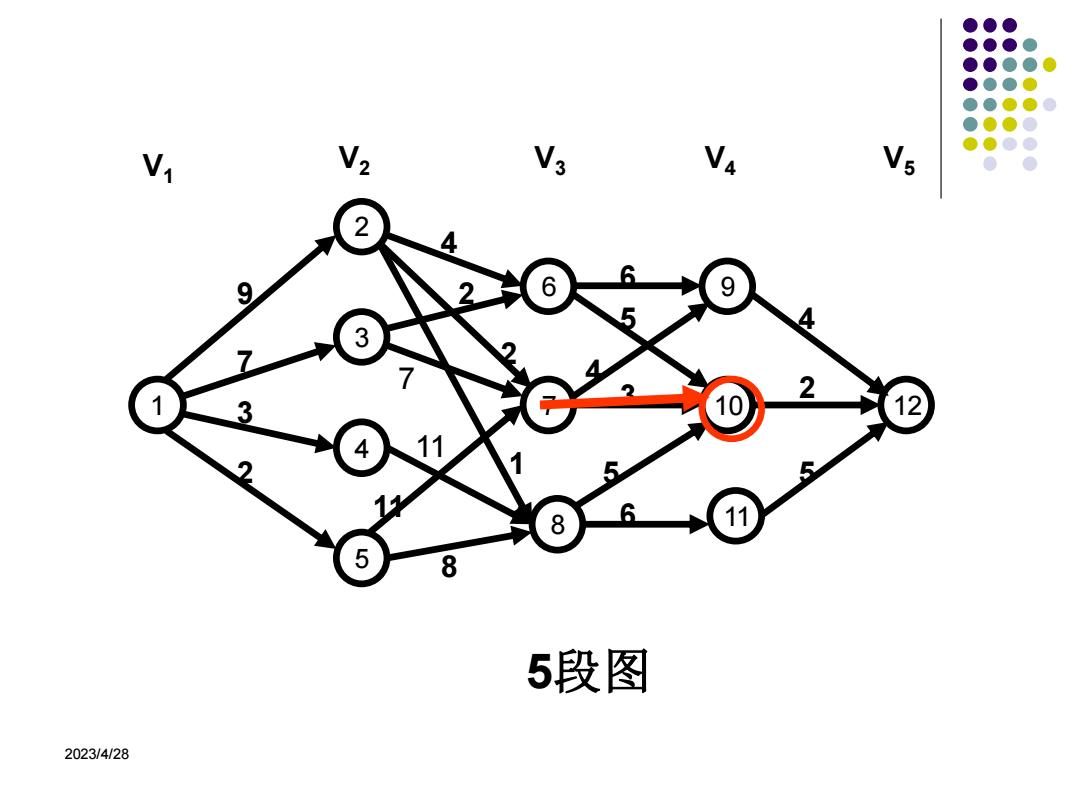
V N2 V3 Na Vo 2 4 9 9 4 3 7 2 1 3 12 11 2 8 6 5 8 5段图 2023/4/28
2023/4/28 1 2345 678 9 10 11 12 9732 4 2 2 7 11 11 8 1 4 563 5 6 425 V 1 V 2 V 3 V 4 V 5 5段图

★各递推结果 第4段 C0ST(4,9)=c(9,12)=4 C0ST(4,10)=c(10,12)=2 C0ST(4,11)=c(11,12)=5 第3段 coST(3,6)=min{6+C0ST(4,9),5+C0ST(4,10)}=7 C0ST(3,7)=min{4+C0ST(4,9),3+COST(4,10)}=5 C0ST(3,8)=min{5+C0ST(4,10),6+C0ST(4,11)}=7 第2段 C0ST(2,2)=min{4+C0ST(3,6),2+COST(3,7), 1+C0ST(3,8)}=7 C0ST(2,3)=9 C0ST(2,4)=18 C0ST(2,5)=15 第1段 C0ST(1,1)=min{9+C0ST(2,2),7+C0ST(2,3): 3+C0ST(2,4),2+C0ST(2,5)} =16 S到t的最小成本路径的成本=16 2023/4/28
2023/4/28 ★各递推结果 第4段 COST(4,9) = c(9,12) = 4 COST(4,10) = c(10,12) = 2 COST(4,11) = c(11,12) = 5 第3段 COST(3,6) = min{6+COST(4,9),5+COST(4,10)} = 7 COST(3,7) = min{4+COST(4,9),3+COST(4,10)} = 5 COST(3,8) = min{5+COST(4,10),6+COST(4,11)} = 7 第2段 COST(2,2) = min{4+COST(3,6) , 2+COST(3,7), 1+COST(3,8)} = 7 COST(2,3) = 9 COST(2,4) = 18 COST(2,5) = 15 第1段 COST(1,1) = min{9+COST(2,2),7+COST(2,3), 3+COST(2,4),2+COST(2,5)} = 16 S到t的最小成本路径的成本 = 16