
3.2二分检索(折半查找) 1.问题的描述 已知一个按非降次序排列的元素表a, a2,,an,判定某给定的元素x是否在该表中出 现。 若是,则找出x在表中的位置并返回其所在下标 > 若非,则返回0值
3.2 二分检索(折半查找) 1. 问题的描述 已知一个按非降次序排列的元素表a1 , a2 , …,an ,判定某给定的元素x是否在该表中出 现。 ➢ 若是,则找出x在表中的位置并返回其所在下标 ➢ 若非,则返回0值

分治求解策略分析: 定义问题的形式描述:=(n,a1,a2,,anX) 冬 问题分解:选取下标k,由此将分解为3个子问题: l1=(k-1,a1,a2,,ak-1X) l2=(1,akX) I3=(n-k,ak+1,ak+2,...,an,x) 对于2,若ak=x,则有解k,对l、l3不用再求解;否则, 若x<ak,则只在l中求解,对l3不用求解; 若x>ak,则只在3中求解,对l不用求解; 11、3上的求解可再次采用分治方法划分后求解 (递归过程) k的不同选择策略导致不同的检索算法:二分检 索,Fibonacci检索,线性插值检索,随机检索
分治求解策略分析: ❖ 定义问题的形式描述:I=(n, a1 , a2 , …,an ,x) ❖ 问题分解:选取下标k,由此将I分解为3个子问题: I1=(k-1, a1 , a2 , …,ak-1 ,x) I2=(1, ak ,x) I3=(n-k, ak+1, ak+2, …,an ,x) ➢ 对于I2,若ak=x,则有解k,对I1、I3不用再求解;否则, ➢ 若x<ak,则只在I1中求解,对I3不用求解; ➢ 若x>ak,则只在I3中求解,对I1不用求解; I1 、I3上的求解可再次采用分治方法划分后求解 (递归过程) k的不同选择策略导致不同的检索算法:二分检 索,Fibonacci检索,线性插值检索,随机检索

2.二分检索算法 算法3.3二分检索 procedure BINSRCH(A,n,x,j) 注: integer low,high,mid,j,n; 给定一个按非降次 lowk-1;high←-n; 序排列的元素数组 while lowshigh do mid←-L(ow+high/2」 A(1:n),n≥1,判断x case 是否出现。 :x<A(mid):high-mid-1 x>A(mid):low←-mid+1 若是,置j,使得 :else:j-mid;return x=A(j) endcase 若非,j=0 repeat j←0 end NIBSRCH
2. 二分检索算法 算法3.3 二分检索 procedure BINSRCH(A,n,x,j) integer low,high,mid,j,n; low←1; high←n; while low≤high do mid ← case :x<A(mid):high←mid-1 :x>A(mid):low ←mid+1 :else:j←mid;return endcase repeat j ← 0 end NIBSRCH(low + high)/2 注: 给定一个按非降次 序排列的元素数组 A(1:n),n≥1,判断x 是否出现。 •若是,置j,使得 x=A(j) •若非,j=0
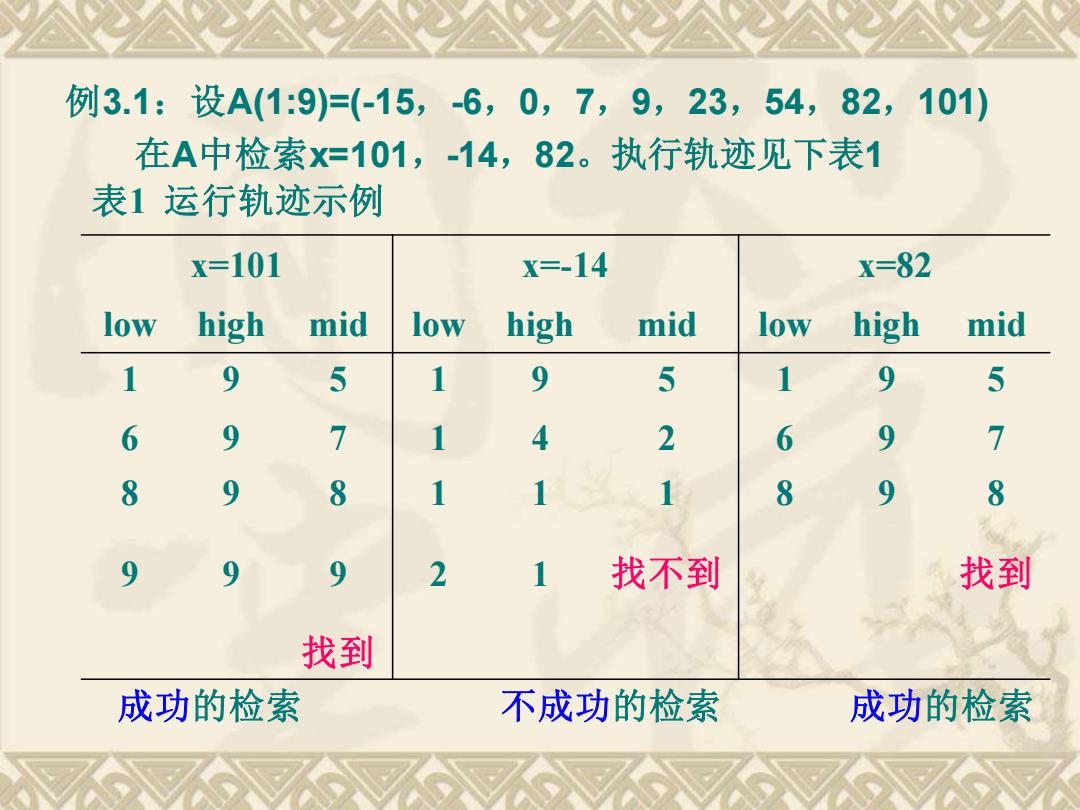
例3.1:设A(1:9)=(-15,-6,0,7,9,23,54,82,101) 在A中检索X=101,-14,82。执行轨迹见下表1 表1运行轨迹示例 x=101 x=-14 x=82 low high mid low high mid low high mid 1 9 5 1 9 5 1 9 5 6 9 7 1 4 2 6 9 7 8 9 8 1 1 8 9 8 9 9 9 2 1 找不到 找到 找到 成功的检索 不成功的检索 成功的检索
例3.1:设A(1:9)=(-15,-6,0,7,9,23,54,82,101) 在A中检索x=101,-14,82。执行轨迹见下表1 表1 运行轨迹示例 x=101 x=-14 x=82 low high mid low high mid low high mid 1 9 5 1 9 5 1 9 5 6 9 7 1 4 2 6 9 7 8 9 8 1 1 1 8 9 8 9 9 9 2 1 找不到 找到 找到 成功的检索 不成功的检索 成功的检索

3.算法的正确性证明 定理3.1过程BINSRCH(A,n,x,j)能正确运行 证明: 1)在具体指定A中的数据元素及x的数据类型后,算法中的所有 运算都能按要求正确运行一即首先满足确定性和能行性 2)终止性 算法初始部分置Iowk-1,high←-n ①若n=0,不进入循环,置0,算法终止 ②否则,进入循环,计算mid, 或x=A(mid),j置为mid,算法终止; 或x<A(mid),置high←-mid-1,搜索范围实际缩小为[low,mid-1], 进入下次循环,对mid+1,high区间不做进一步搜索; 或x>A(mid),置Iow←-mid+1,进入下次循环;搜索范围实际缩小 为[mid+1,high],对[low,mid-1]区间不做进一步搜索; 因Iow,high,mid都是整型变量,故按照上述规则,在有限步内,或找到 某个mid,有Amid)=x;或变得Iow心high,在A中没有找到任何元素等于x, 算法终止
3. 算法的正确性证明 定理3.1 过程BINSRCH(A,n,x,j)能正确运行 证明: 1)在具体指定A中的数据元素及x的数据类型后,算法中的所有 运算都能按要求正确运行——即首先满足确定性和能行性 2)终止性 算法初始部分置low←1, high←n ① 若n=0,不进入循环,j置0,算法终止 ② 否则,进入循环,计算mid, ➢ 或 x=A(mid),j置为mid,算法终止; ➢ 或x<A(mid),置high←mid-1,搜索范围实际缩小为[low, mid-1], 进入下次循环,对[mid+1, high]区间不做进一步搜索; ➢ 或x>A(mid),置low←mid+1,进入下次循环;搜索范围实际缩小 为[mid+1, high],对[low, mid-1]区间不做进一步搜索; 因low, high, mid都是整型变量,故按照上述规则,在有限步内,或找到 某个mid,有A(mid) = x;或变得low>high,在A中没有找到任何元素等于x, 算法终止