
10.1引 言 记号A<:B将用来表示A是B的子类型 断言A<:B的含义有两种一般的观点 1、类型A的值的每种表示都是类型B的值的一种表 示 2、类型A的值的每种表示都可以按某种“标准”的 方式转换成类型B的值的一种表示 本章观点 一种语言和它的子定型性质可以由一组规则来定义 子定型是类型之间的关系,而继承性是实现 之间的关系
10.1 引 言 • 记号A<:B将用来表示A是B的子类型 • 断言A<:B的含义有两种一般的观点 1、类型A的值的每种表示都是类型B的值的一种表 示 2、类型A的值的每种表示都可以按某种“标准”的 方式转换成类型B的值的一种表示 • 本章观点 一种语言和它的子定型性质可以由一组规则来定义 • 子定型是类型之间的关系,而继承性是实现 之间的关系

10.2有子定型的简单类型化入演算 本节用子定型来拓展入→, 得到演算 -用它来讨论子定型的一些本质特征 笛卡儿积、和、unit及ul可以加入而不会使它变 得复杂 个入之基调是一个三元组Σ=〈B,SWb,C〉 -B是类型常量集合 C是项常量的集合 Sub是类型常量b,b'∈B之间的子定型断言b<:b'的 集合
10.2 有子定型的简单类型化演算 • 本节用子定型来拓展→,得到演算<: – 用它来讨论子定型的一些本质特征 – 笛卡儿积、和、unit及null可以加入而不会使它变 得复杂 • 一个<:基调是一个三元组 = B, Sub, C – B是类型常量集合 – C是项常量的集合 – Sub是类型常量b, bB之间的子定型断言b <:b的 集合 → →

10.2有子定型的简单类型化入演算 1、类型 入的类型表达式和入的类型表达式一样 t::=b t->t -入之独有的特征 t<:t (ref<:) p<:0,0<:T 0<: (trans <: 它们是所考虑的每个子定型系统的一部分,它使 得子类型关系是一个前序关系
10.2 有子定型的简单类型化演算 1、类型 – <:的类型表达式和→的类型表达式一样 ::= b | → – <:独有的特征 <: (ref <:) (trans <:) 它们是所考虑的每个子定型系统的一部分,它使 得子类型关系是一个前序关系 <:, <: <: → →

10.2有子定型的简单类型化入演算 在每个系统中,对每种类型形式,至少有一 条公理或推理规则,用来标识这种类型形式 的子定型性质 -对于函数类型有 p<:t,t<:p (→ →T<:p→p →对第二个变元是单调的,但是对第一个变元是 反单调的
10.2 有子定型的简单类型化演算 • 在每个系统中,对每种类型形式,至少有一 条公理或推理规则,用来标识这种类型形式 的子定型性质 – 对于函数类型有 (→ <:) →对第二个变元是单调的,但是对第一个变元是 反单调的 <:, <: → <: →
10.2有子定型的简单类型化入演算 。一个简单示例:it<:real引起的下列安排 int→reml int→int real→real real→int 把int→int解释成一个函数集合,这些函数的定 义域至少是所有整数的集合
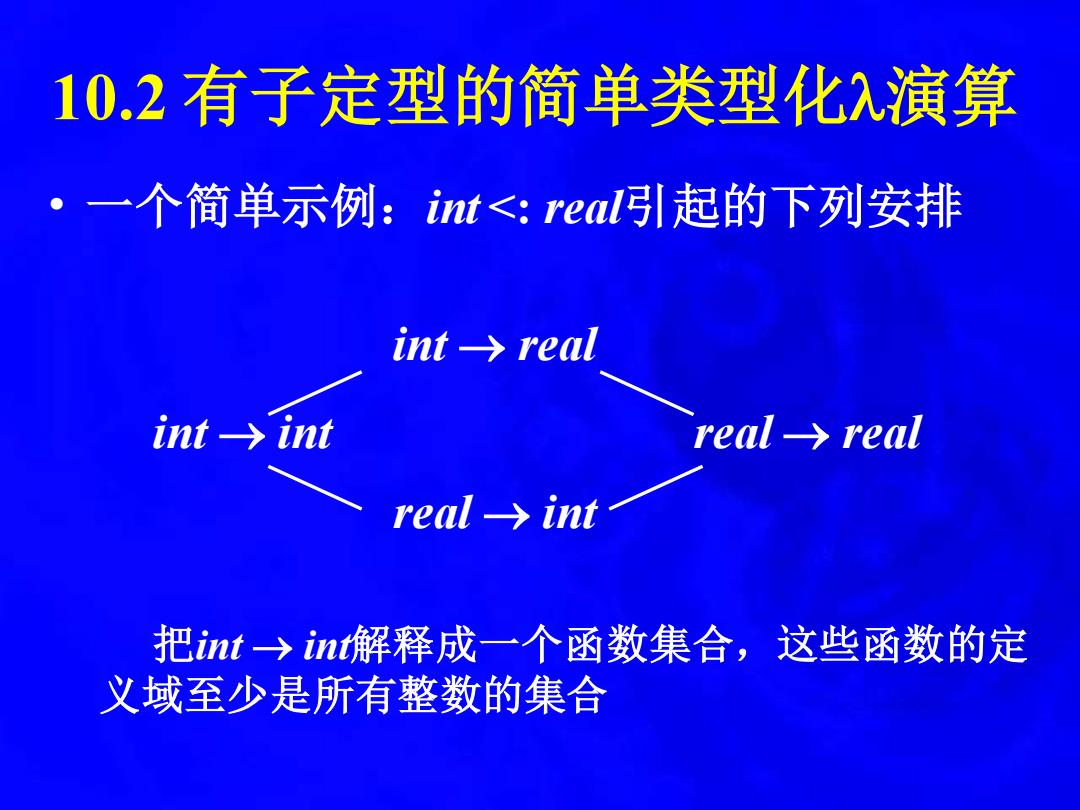
10.2 有子定型的简单类型化演算 • 一个简单示例:int <: real引起的下列安排 int → real int → int real → real real → int 把int → int解释成一个函数集合,这些函数的定 义域至少是所有整数的集合